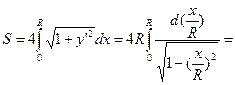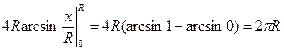Вычисление площади криволинейной трапеции заданной в параметрической форме

Пусть функция y=f(x) на отрезке [a,b] задана параметрически

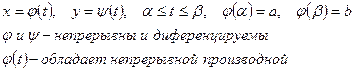
Следовательно, площадь криволинейной трапеции может быть вычислена по формуле

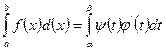
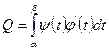
Пример. Вычислить площадь эллипса.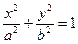

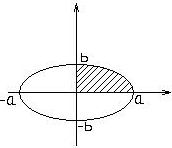Эллипс- фигура симметричная по всем осям, для вычисления площади эллипса достаточно вычислить площадь заштрихованной части. Используя тригонометрическую параметризацию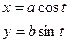 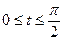, получим

.

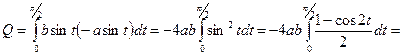
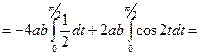
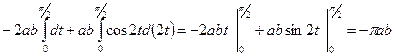
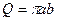Площадь криволинейного сектора

В полярной системе координат положение точки на плоскости определяется парой чисел: 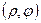. Число 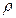определяет расстояние от точки М до полюса. 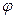- угол образованный отрезком ОМ и полярной осью.

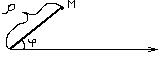
Если полюс совпадает с началом декартовой системы координат, а ось х совпадает с полярной осью, то между декартовой и полярной системами координат, существует связь.

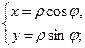
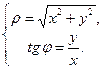
При нахождении 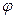нужно учитывать, в какой четверти находится точка, и брать соответствующее значение.

В полярной системе координат уравнение кривой может быть записано в ви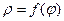де

где 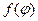- непрерывная функция, .

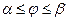Находясь в полярной системе координат, получим выражение для площади сектора ОАВ ограниченного кривой 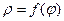и радиус векторами 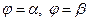. Разобьём данную область радиус – векторами 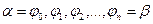на n – частей. Обозначим через 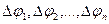- углы между радиус векторами.

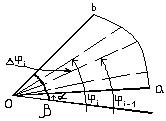
Обозначим через 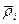-некоторый радиус-вектор, соответствующий углу , .

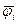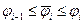Рассмотрим круговой сектор с радиусом 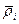и центральным углом 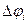. Площадь кругового сектора равна: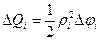

Сумма 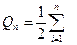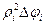= 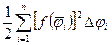даёт площадь ступенчатого сектора. Так как эта сумма является интегральной суммой для функции 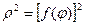на отрезке 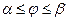, то её предел есть неопределённый интеграл 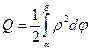. Выписанный интеграл считают площадью криволинейного сектора ОАВ.

Длина дуги кривой

Длина дуги кривой в декартовой прямоугольной системе координат.

Пусть в прямоугольных координатах на плоскости дана кривая 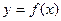заданная на отрезке 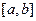. Функция 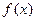- обладает непрерывной производной на отрезке 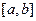. Найдём длину дуги АВ этой кривой, заключённой между вертикальными прямыми 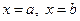. Возьмём на дуге АВ точки 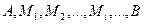с абсциссами .

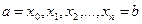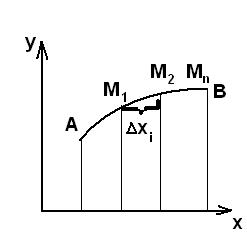Соединим выбранные точки хордами, получим ломаную линию, вписанную в дугу .

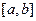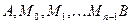. длина ломаной 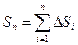. Длиной S дуги называется тот предел, к которому стремится длина вписанной ломаной, когда длина её наибольшего звена стремится к нулю.

.

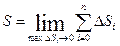Покажем, что предел существует.

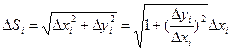
Рассматриваемая функция 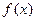удовлетворяет всем условиям теоремы Лагранжа. Согласно этой теоремы .

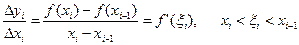Следовательно, .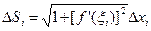

Таким образом, длина ломаной равна .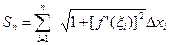

Выписанную сумму можно рассматривать как интегральную сумму на отрезке 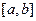. Функция стоящая под знаком суммы непрерывна, согласно сделанным предположениям, и следовательно существует предел интегральной суммы, который равен определённому интегралу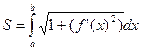

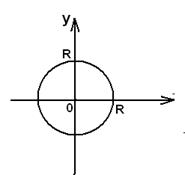Пример:Вычислить длину окружности

.

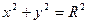
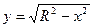
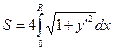
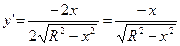Следовательно,