Пункт 2. Предельный переход под знаком интеграла. Непрерывность интеграла как функции параметра
Определение.
Пусть  - это предельная точка множества
- это предельная точка множества  .Функция
.Функция 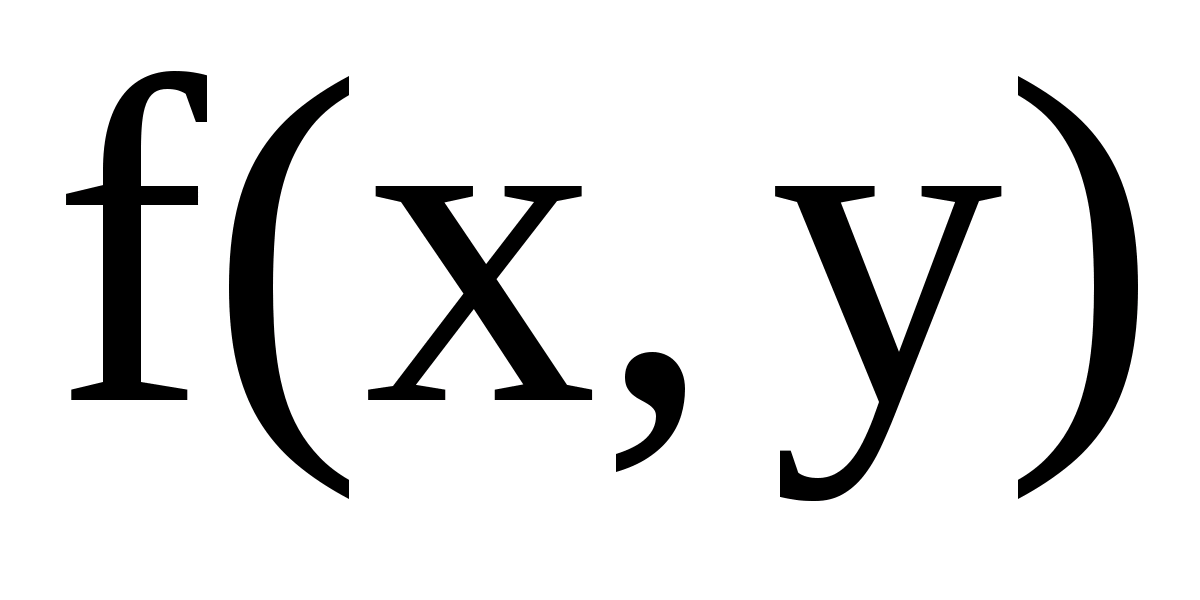 называется равномерно сходящейся к функции
называется равномерно сходящейся к функции  при
при  по переменной
по переменной 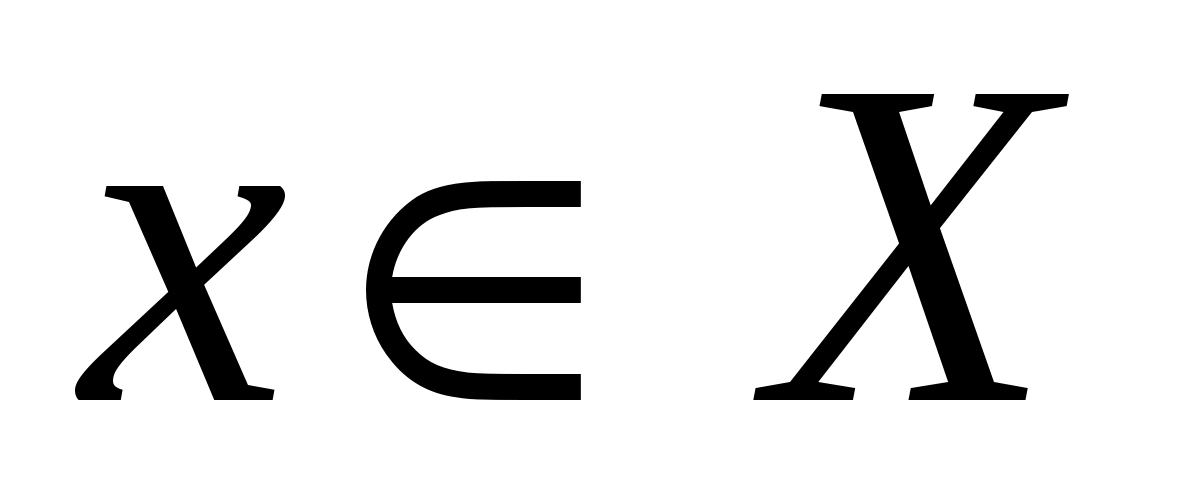 , если выполняются следующие условия:
, если выполняются следующие условия:
1. для 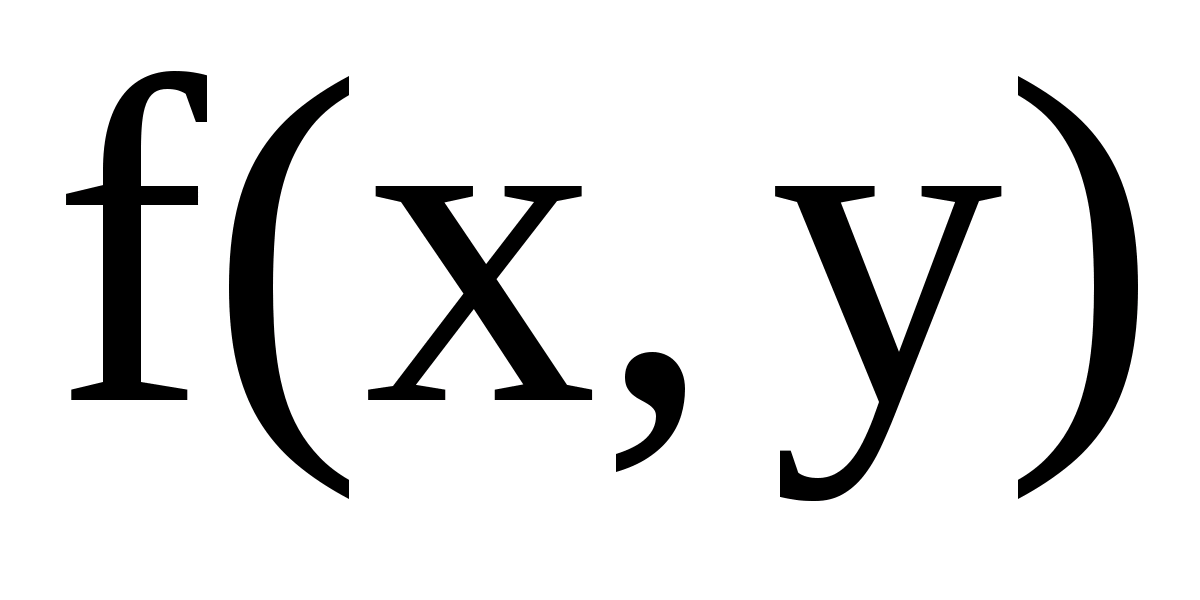 при
при  существует конечная предельная функция
существует конечная предельная функция  ;
;
2. . (1)
Замечание 1.
В цепочки (1)  зависит только от
зависит только от  и не зависит от
и не зависит от 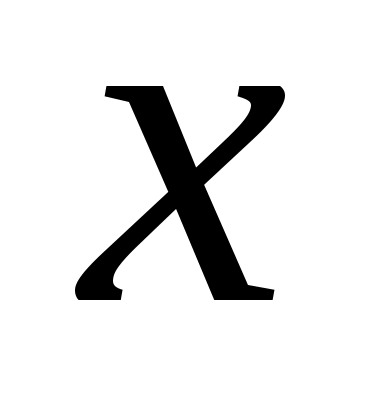 , а неравенство
, а неравенство  выполняется при любых
выполняется при любых 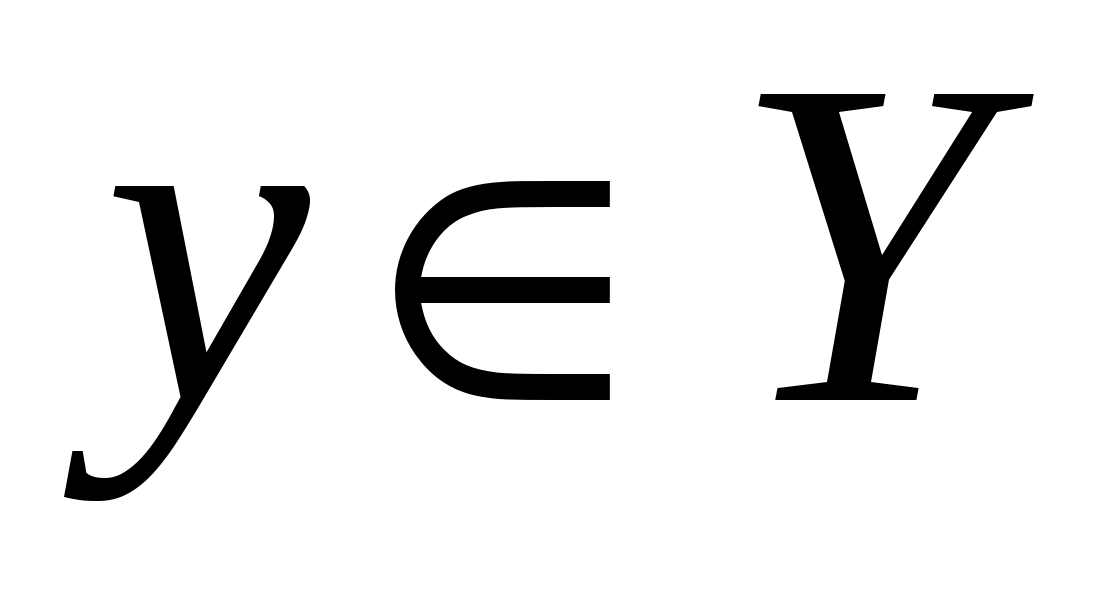 одновременно.
одновременно.
Замечание 2.
Если  , то в цепочке (1) неравенство
, то в цепочке (1) неравенство  следует заменить на
следует заменить на  (
(  ).
).
Теорема 1 (признак сходимости).Если функция 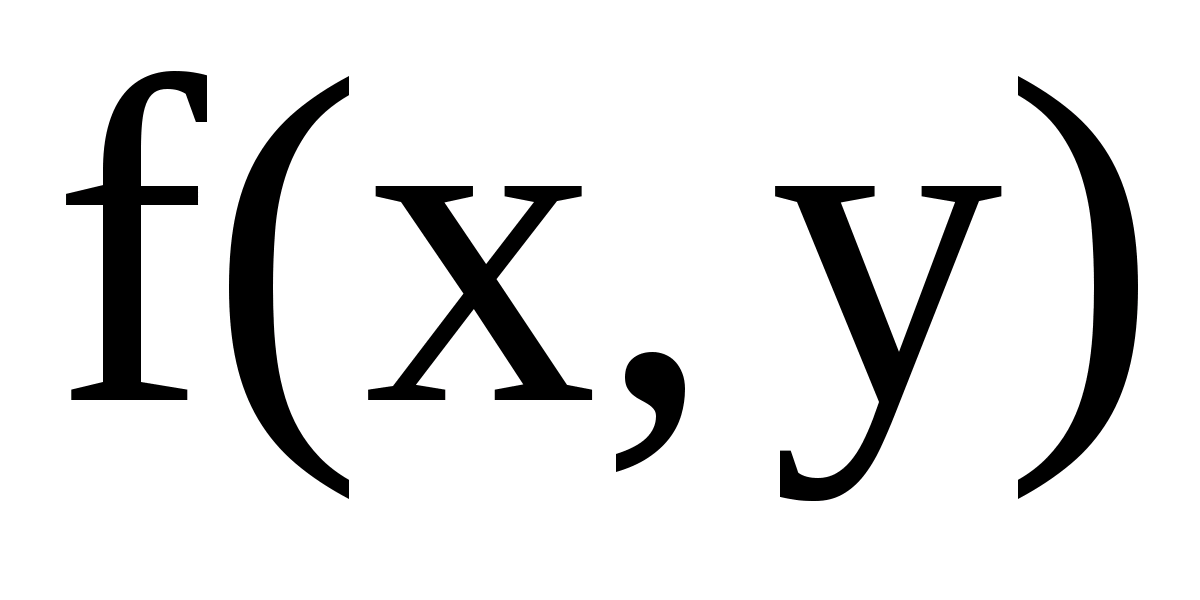 определена на множестве
определена на множестве  , то для того, чтобы она имела предельную функцию и сходилась к ней равномерно необходимо и достаточно, чтобы выполнялась цепочка
, то для того, чтобы она имела предельную функцию и сходилась к ней равномерно необходимо и достаточно, чтобы выполнялась цепочка
 Докажем теорема так.
Докажем теорема так.
Необходимость. Пусть функция 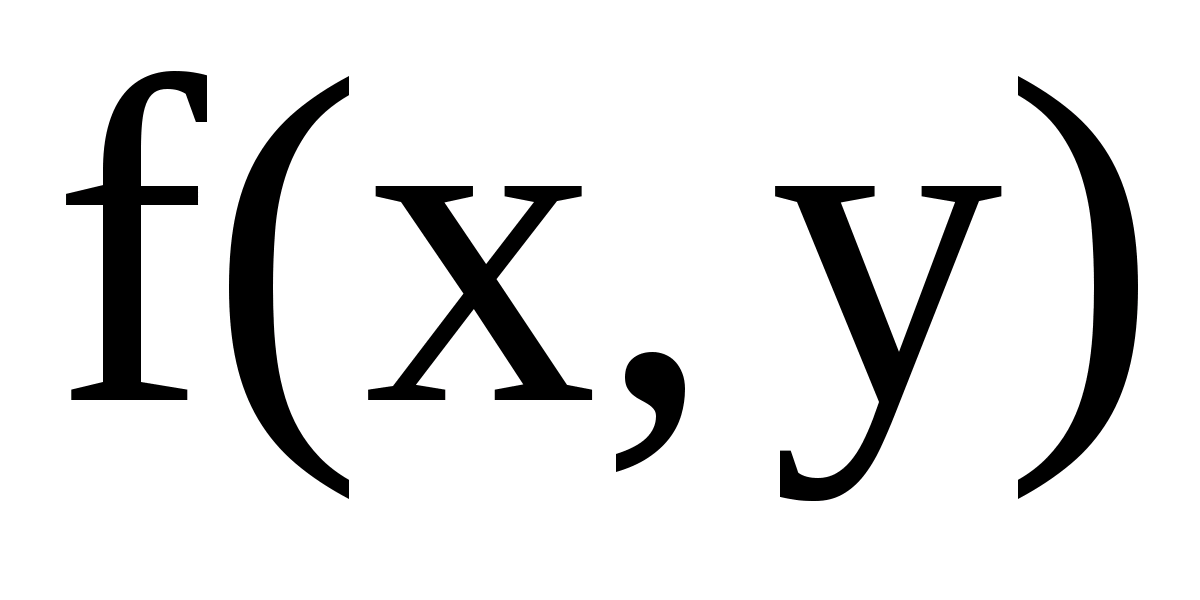 равномерно сходится. Если заменим в определении
равномерно сходится. Если заменим в определении  на
на  и выберем соответственно
и выберем соответственно  , а затем возьмем два значения
, а затем возьмем два значения 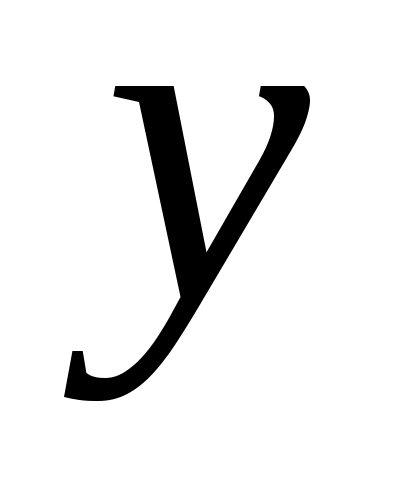 и
и  из
из  так, чтобы выполнялись условия
так, чтобы выполнялись условия  и
и  . В результате получим
. В результате получим 
 и
и  откуда следует последнее неравенство в цепочке
откуда следует последнее неравенство в цепочке  .
.
Достаточность. Теперь пусть существует предельная функция  . Нужно доказать равномерную сходимость функции
. Нужно доказать равномерную сходимость функции 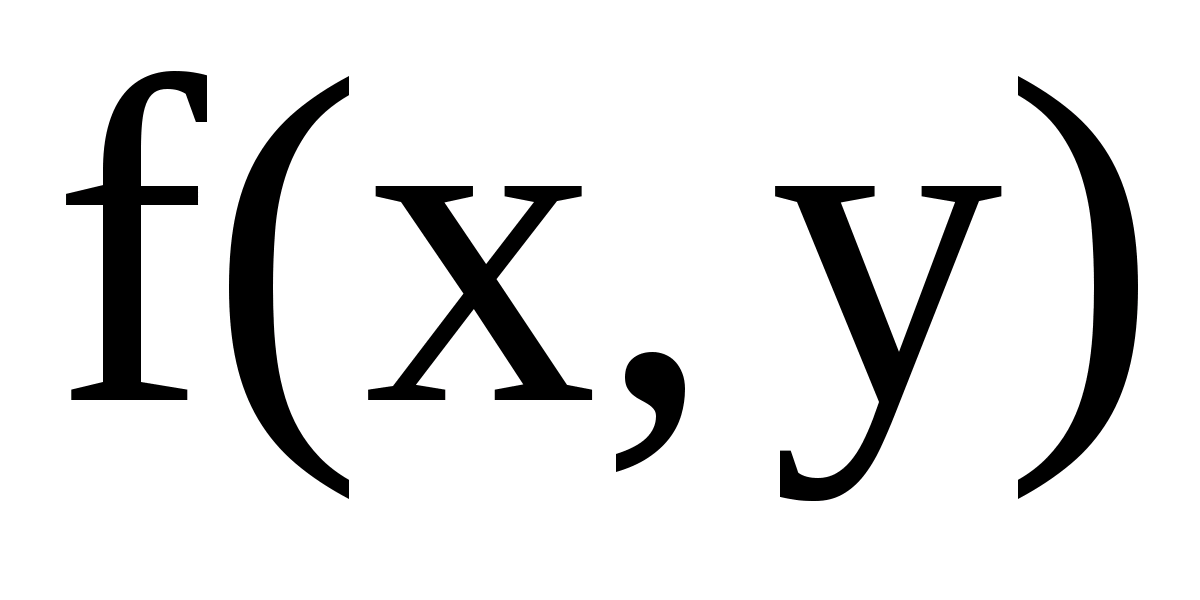 к предельной функции. Для этого совершим переход к пределу в неравенстве
к предельной функции. Для этого совершим переход к пределу в неравенстве  при
при  , получается
, получается  . Что и подтверждает равномерную сходимость
. Что и подтверждает равномерную сходимость 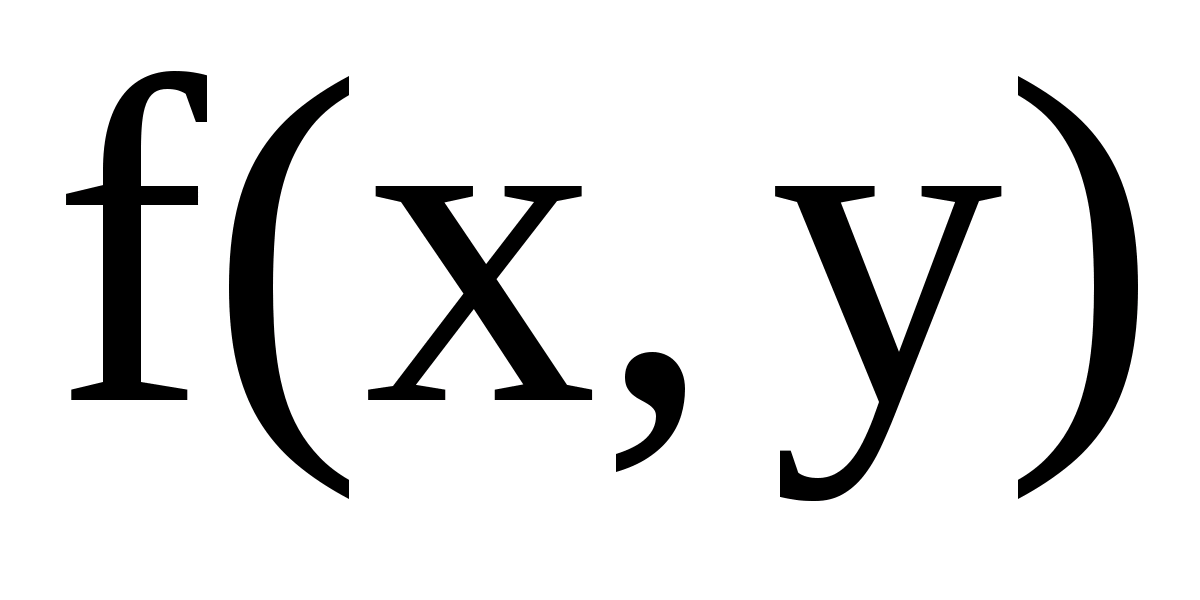 к функции
к функции  .
.
Теорема 2 (о непрерывности предельной функции).Если функция 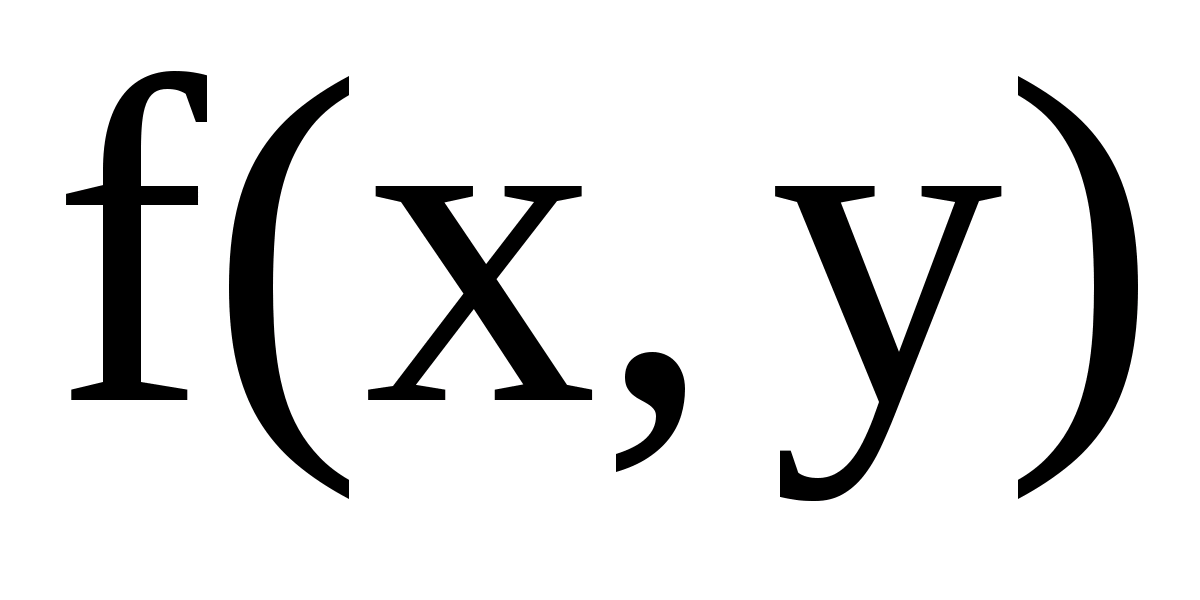 при любом фиксированном
при любом фиксированном 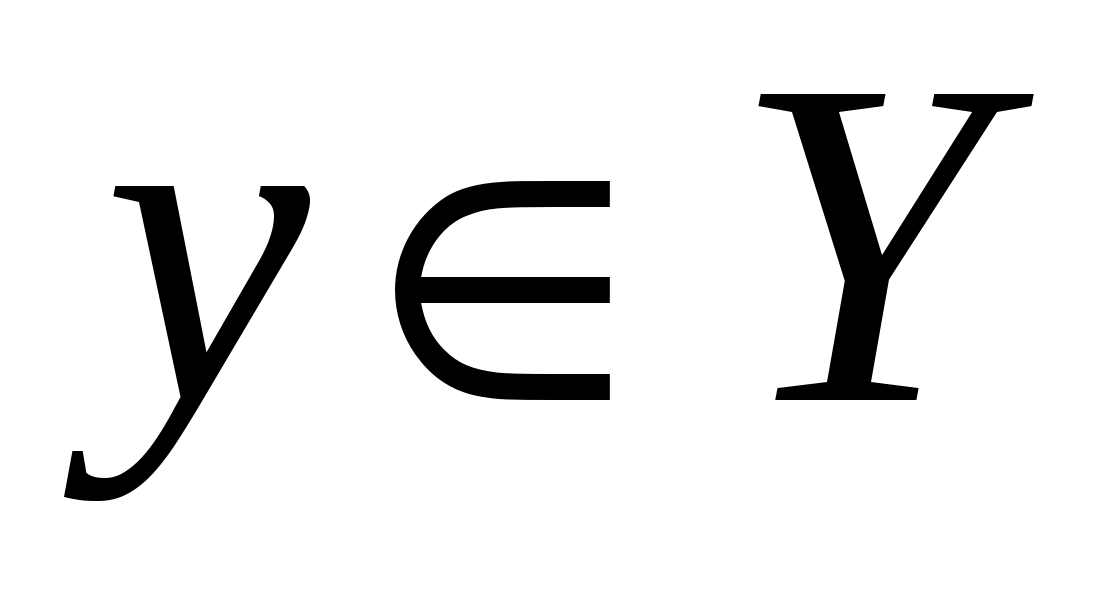 непрерывна на
непрерывна на  и равномерно сходится к предельной функции
и равномерно сходится к предельной функции  по переменной
по переменной 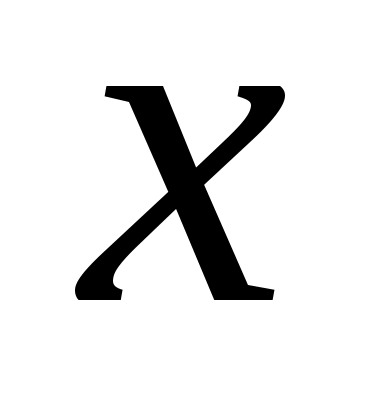 при
при  , то функция
, то функция  также непрерывна на
также непрерывна на 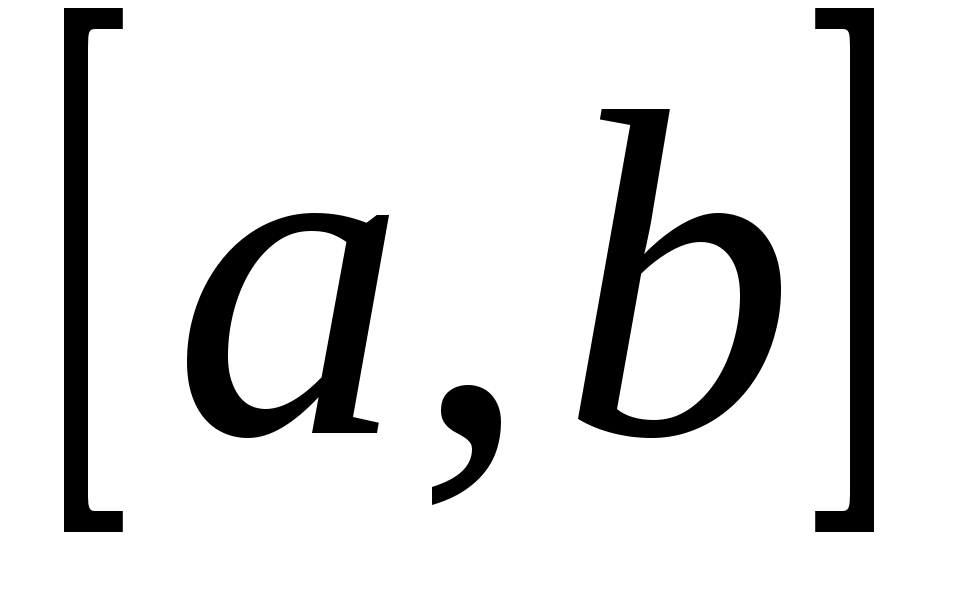 .
.
Легко обобщается теорема Дини: если функция 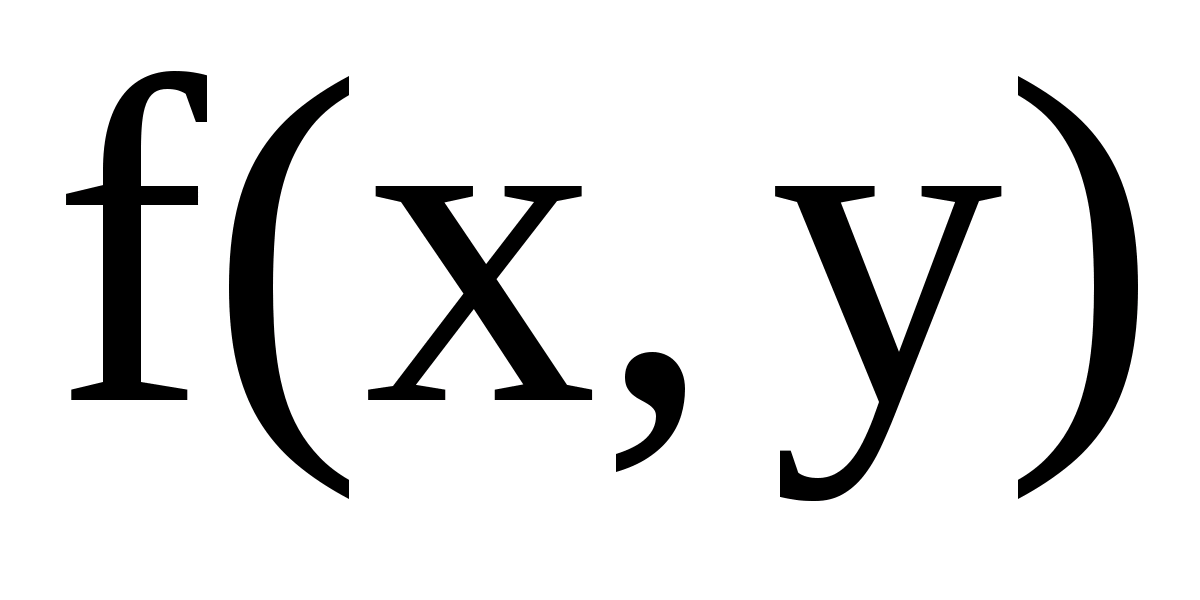 непрерывна для любого фиксированного
непрерывна для любого фиксированного 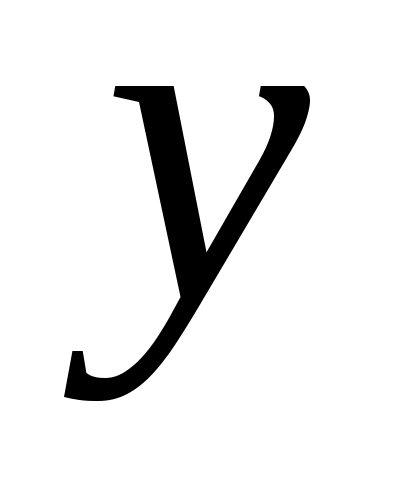 на
на  и при возрастании
и при возрастании 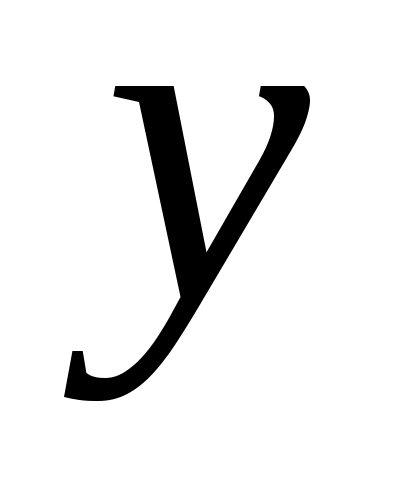 функция, монотонно возрастая, стремится к предельной функции
функция, монотонно возрастая, стремится к предельной функции  , то
, то 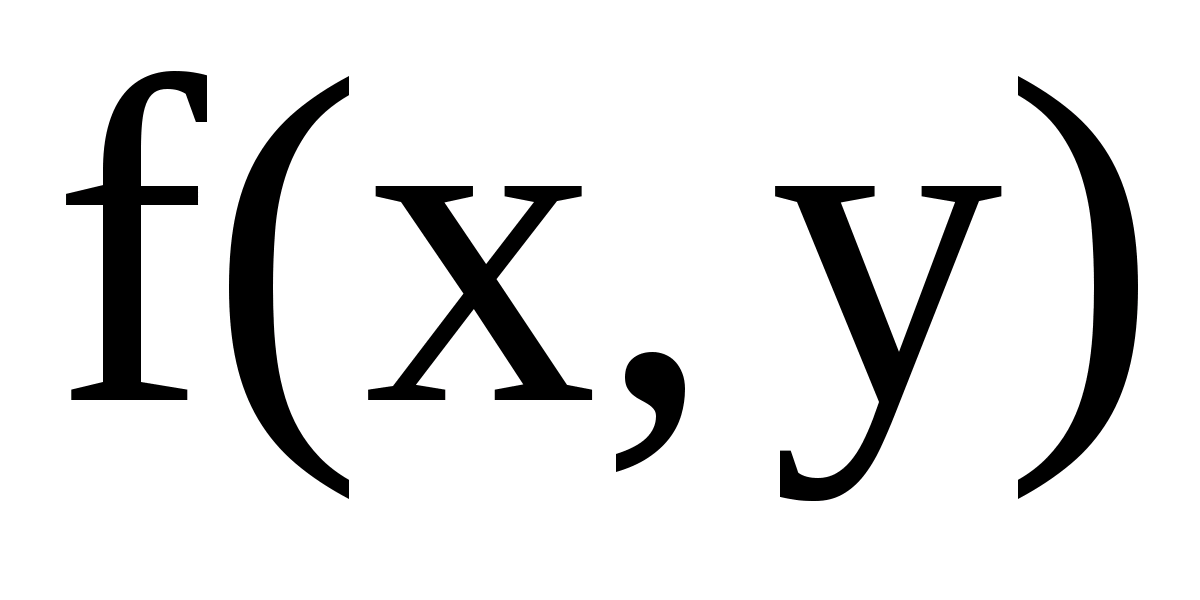 сходится к
сходится к  равномерно.
равномерно.
Теорема 3 (предельный переход по параметру под знаком интеграла).Если функция 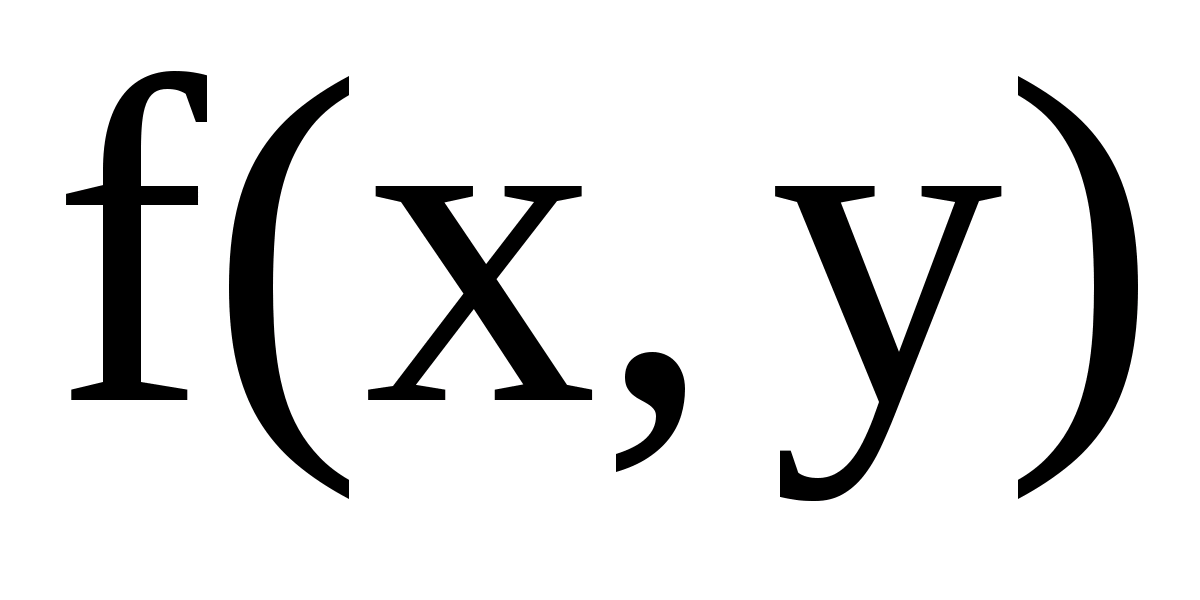 непрерывна при постоянном значении
непрерывна при постоянном значении 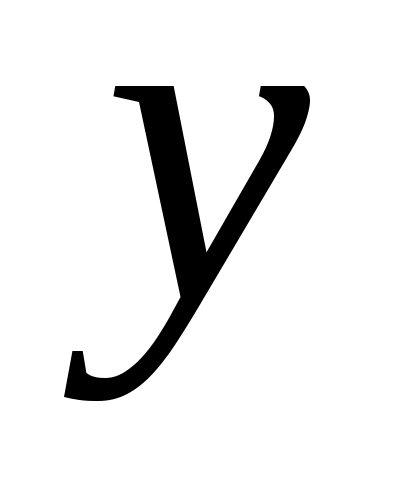 на
на  и сходится равномерно по переменной
и сходится равномерно по переменной 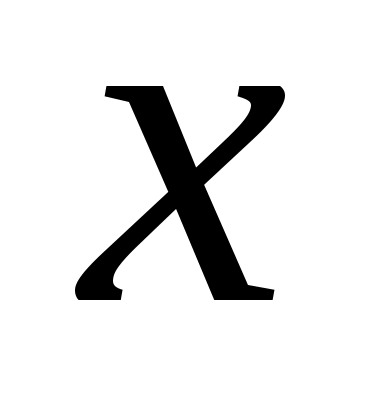 к предельной функции
к предельной функции  при
при  , то тогда имеет место равенство
, то тогда имеет место равенство
 (2)
(2)
Доказательство.
Непрерывность  следует из теоремы 2, значит, она интегрируема на отрезке
следует из теоремы 2, значит, она интегрируема на отрезке 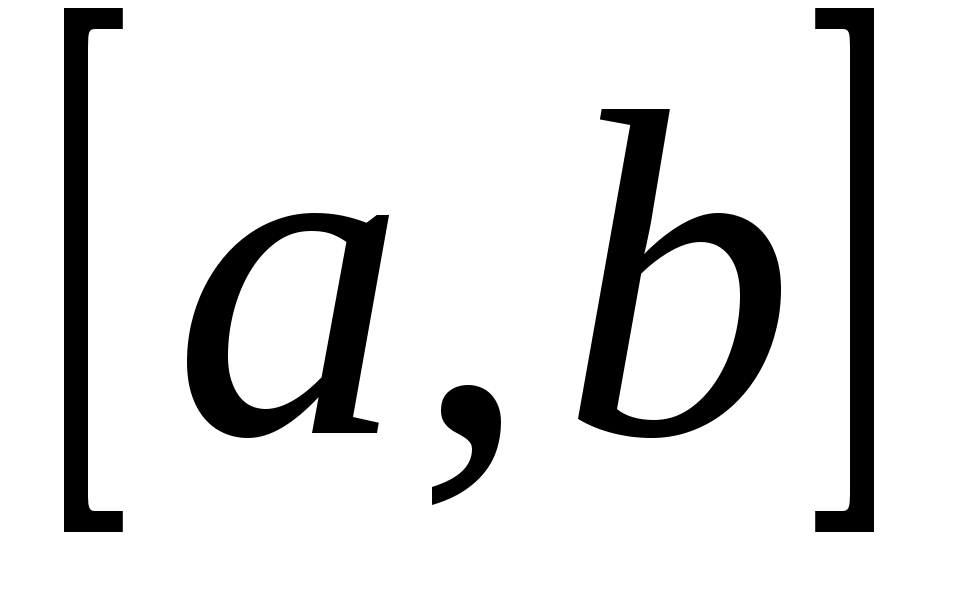 . В силу равномерной сходимости
. В силу равномерной сходимости 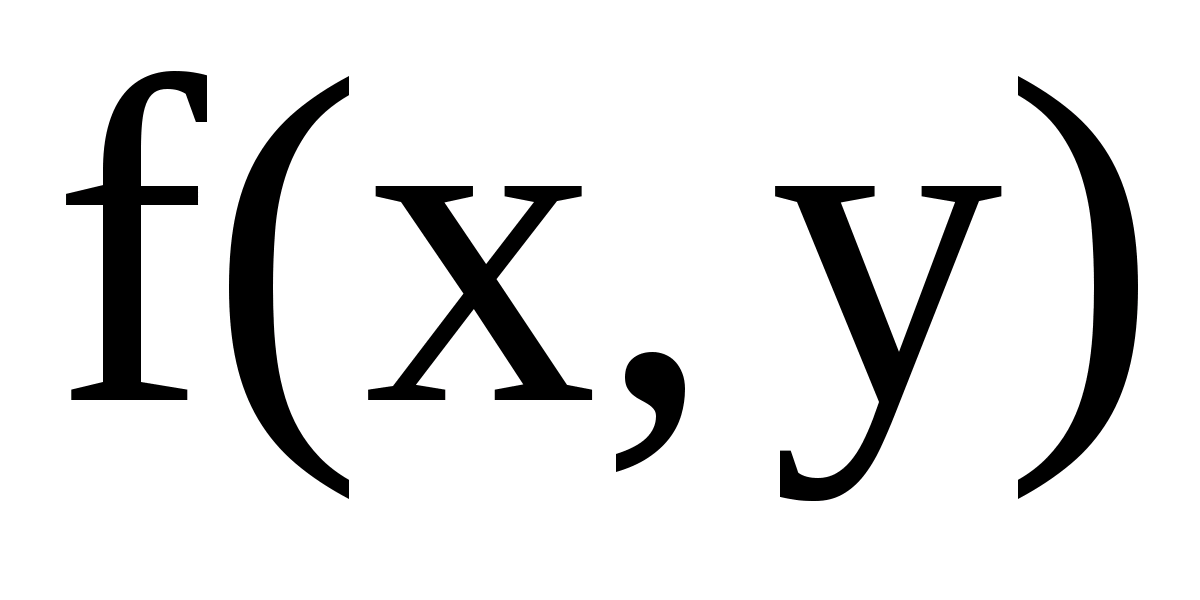 к
к  выполняется
выполняется  . Тогда при тех же
. Тогда при тех же  и
и  имеем:
имеем:
 откуда следует , что доказывает формулу (2).
откуда следует , что доказывает формулу (2).
Замечание 3.
Равенство (2) можно записать и в другом виде
 . (2`)
. (2`)
Следствие 1.
Если функция 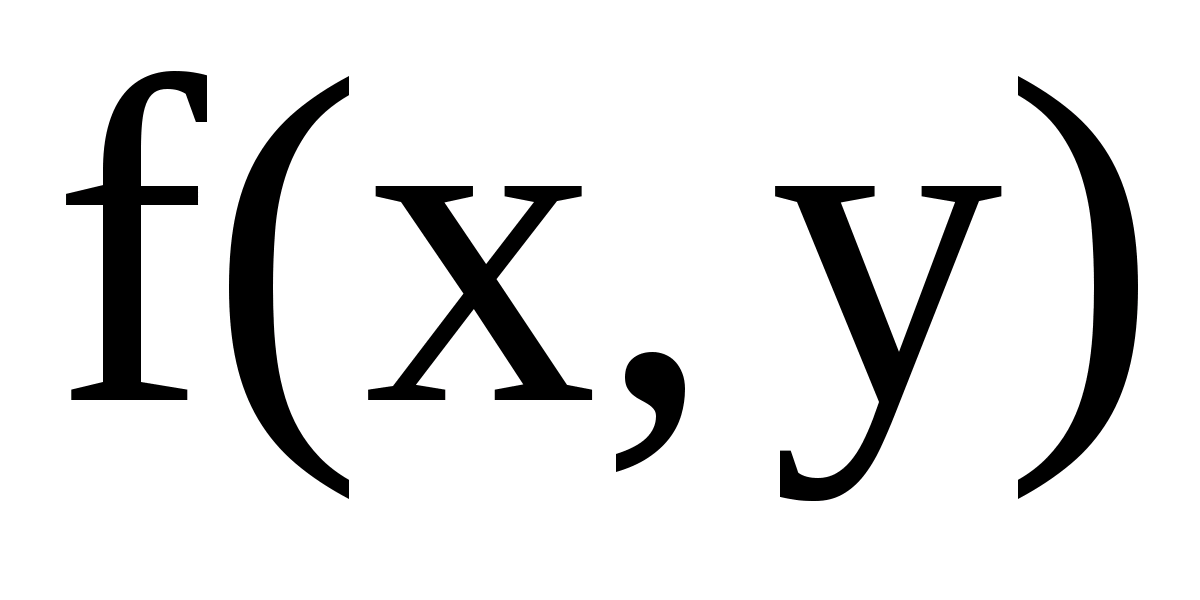 при постоянном
при постоянном 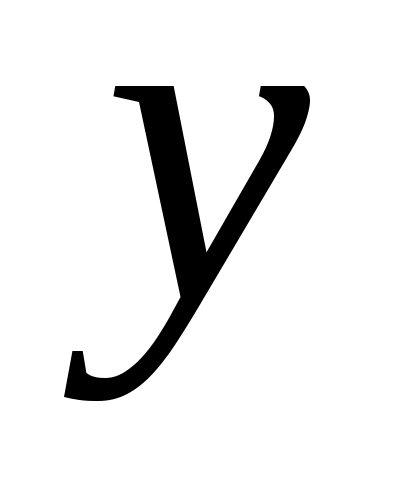 непрерывна по
непрерывна по 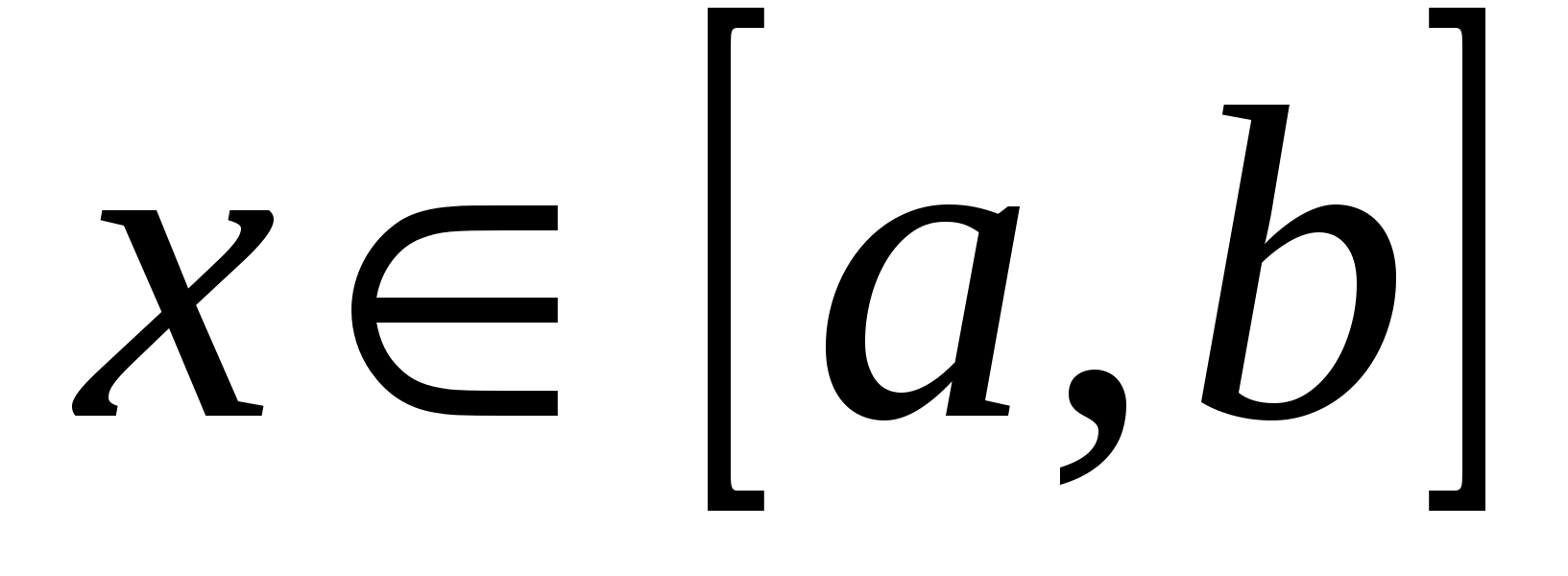 и при возрастании
и при возрастании 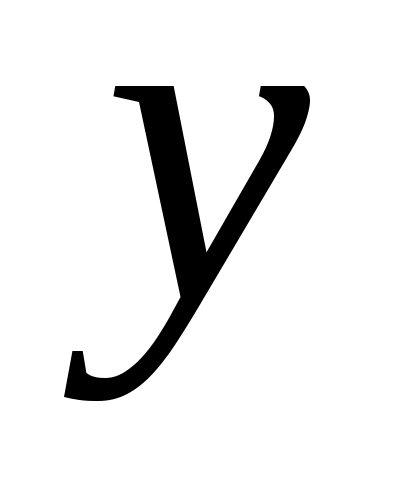 стремится, монотонно возрастая, к непрерывной предельной функции
стремится, монотонно возрастая, к непрерывной предельной функции  , то справедливы формулы (2) и (2`).
, то справедливы формулы (2) и (2`).
В предположении, что область  представляет собой конечный промежуток
представляет собой конечный промежуток  , рассмотрим вопрос о непрерывности функции
, рассмотрим вопрос о непрерывности функции 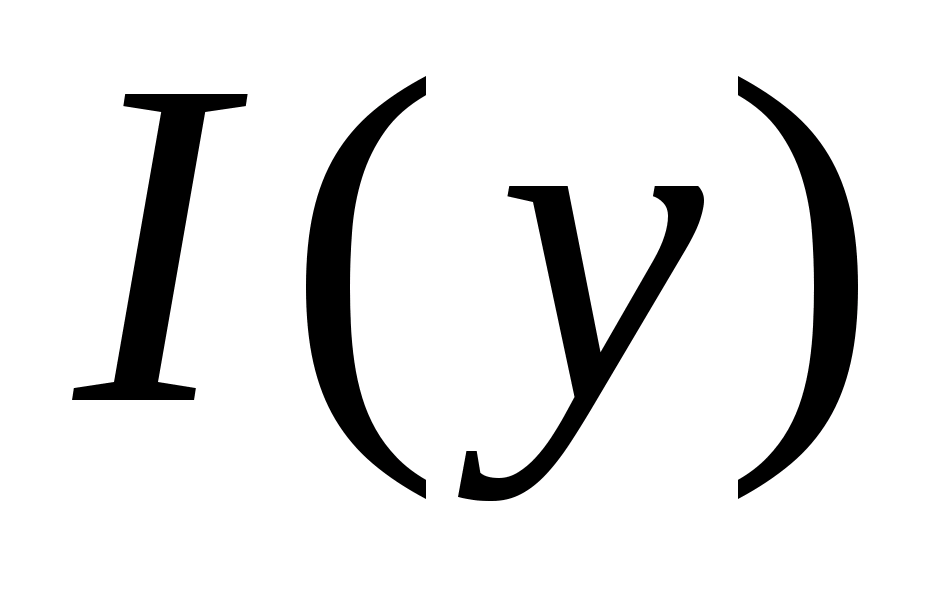 .
.
Пример (№3713 (в)). Найти  .
.
1. функция  непрерывная функция на
непрерывная функция на  . Функции
. Функции  и
и  также непрерывны на .
также непрерывны на .
2. непрерывная функция (т.4 и сл.2) в промежутке 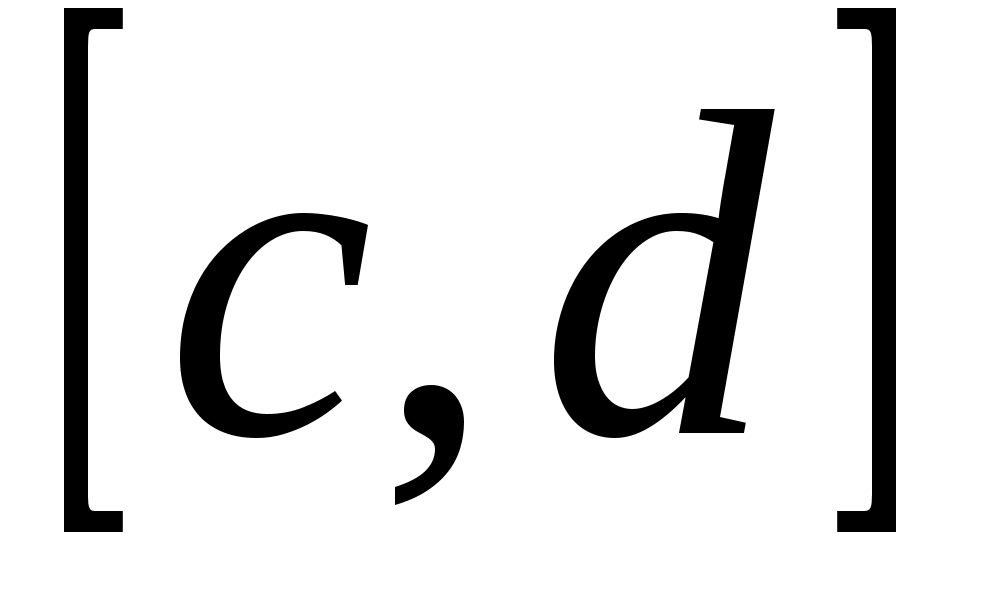 , значит
, значит 
3.  .
.
Теорема 4 (о непрерывности интеграла как функции параметра). Пусть функция 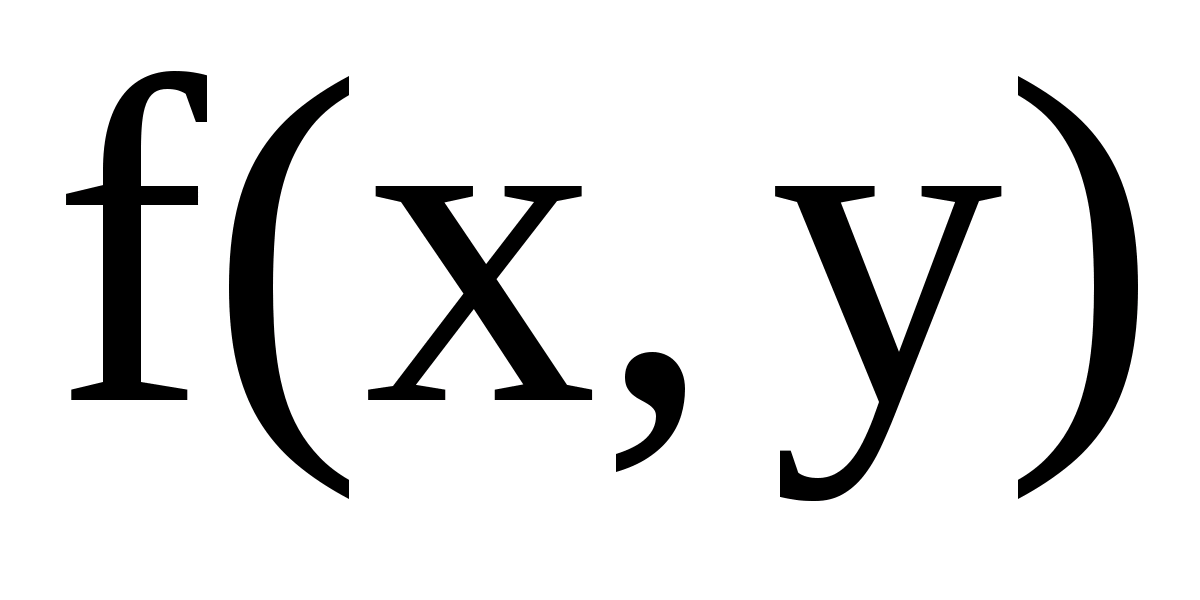 определена и непрерывна в прямоугольнике
определена и непрерывна в прямоугольнике  , тогда интеграл
, тогда интеграл  будет непрерывной функцией от параметра
будет непрерывной функцией от параметра 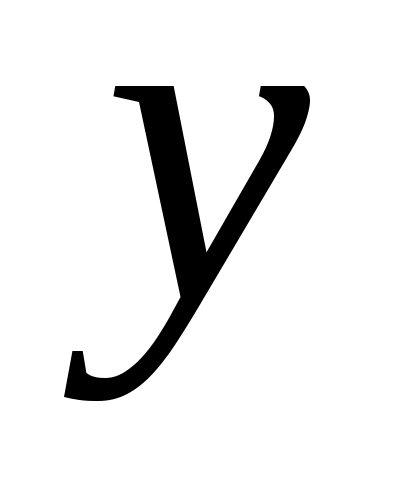 в промежутке
в промежутке 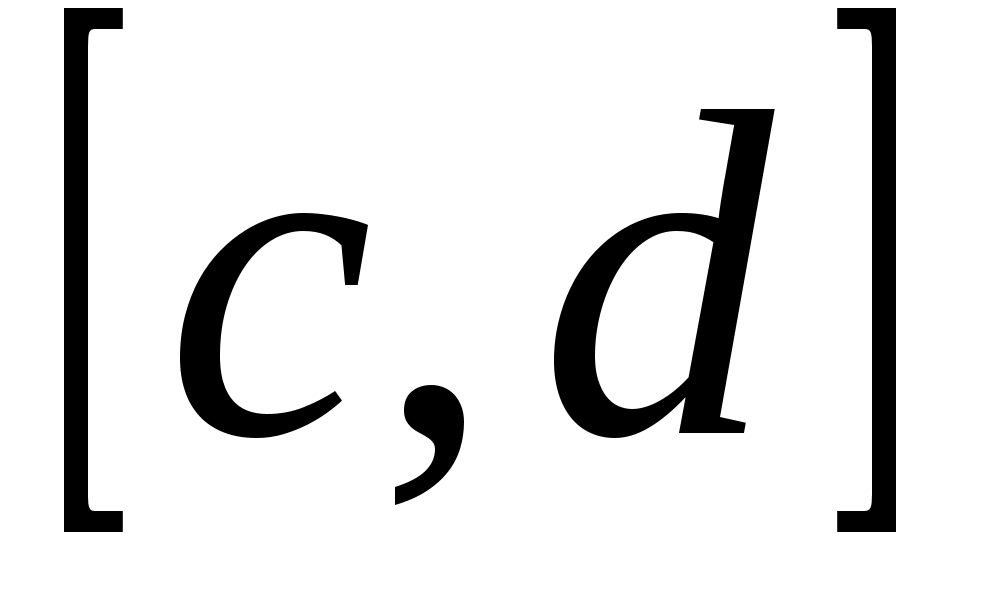 .
.
Доказательство.
Так как 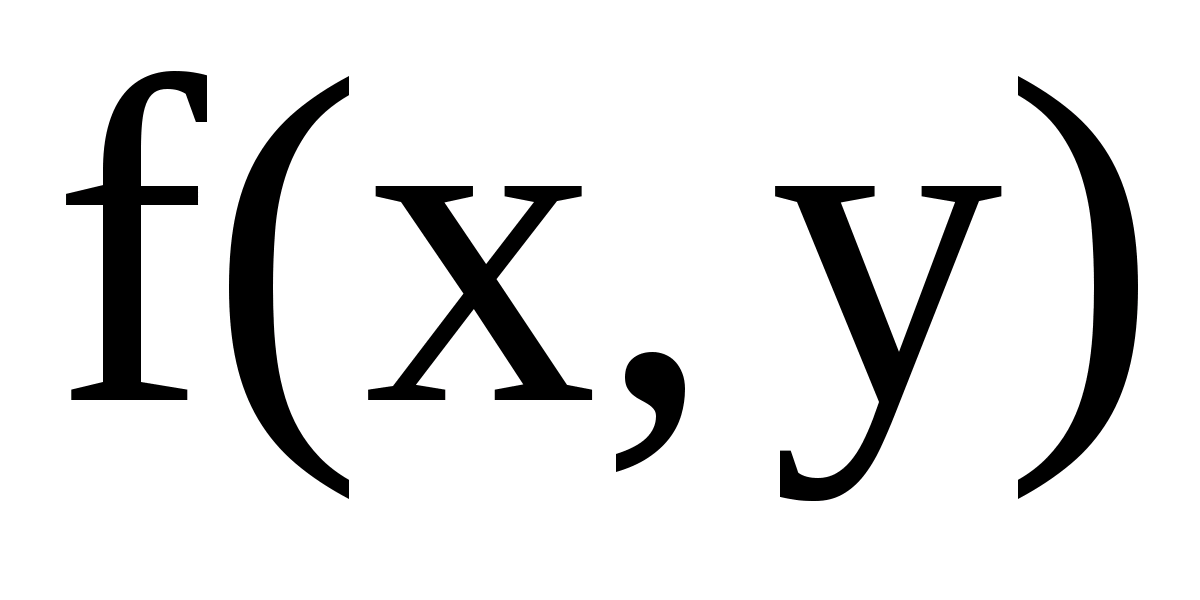 непрерывна на замкнутом множестве, то по теореме Кантора она равномерно непрерывна на данном прямоугольнике
непрерывна на замкнутом множестве, то по теореме Кантора она равномерно непрерывна на данном прямоугольнике  . Возьмем любое
. Возьмем любое  и зафиксируем
и зафиксируем  . Тогда нашему значению
. Тогда нашему значению  будет соответствовать
будет соответствовать  , такое, что для любых двух точек
, такое, что для любых двух точек  ,
,  принадлежащих
принадлежащих  , из неравенств
, из неравенств  и
и  , будет следовать
, будет следовать  . Положим
. Положим  ,
,  , где
, где 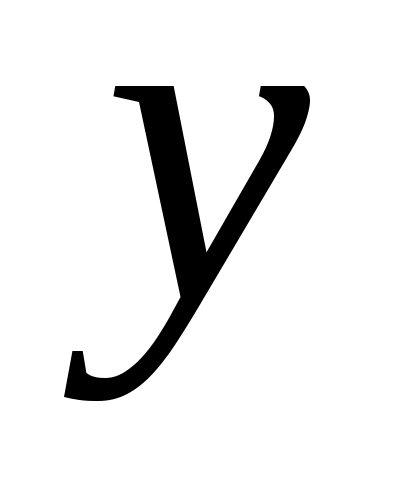 ,
,  - любые из
- любые из 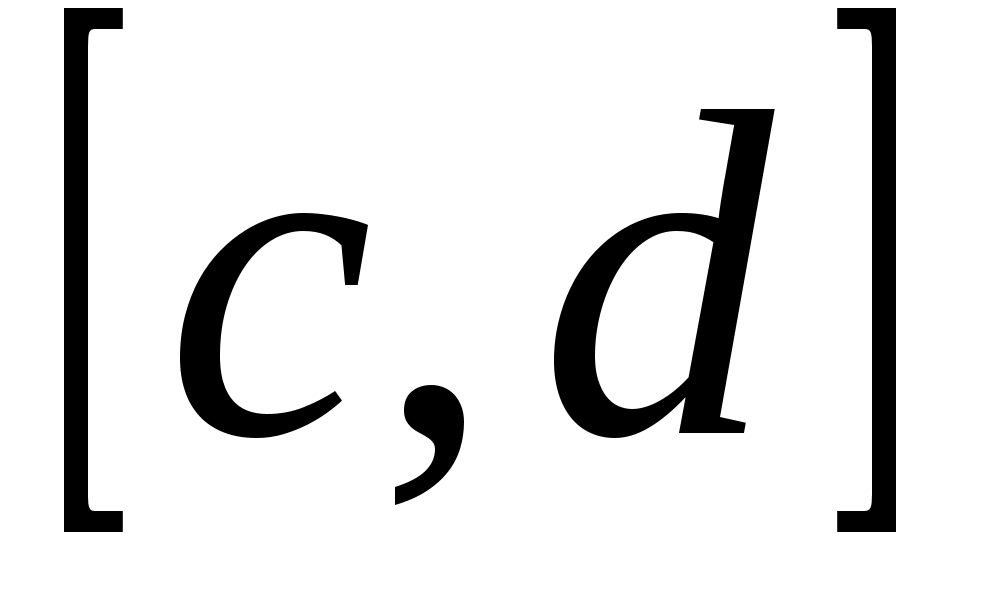 , и
, и  , где
, где 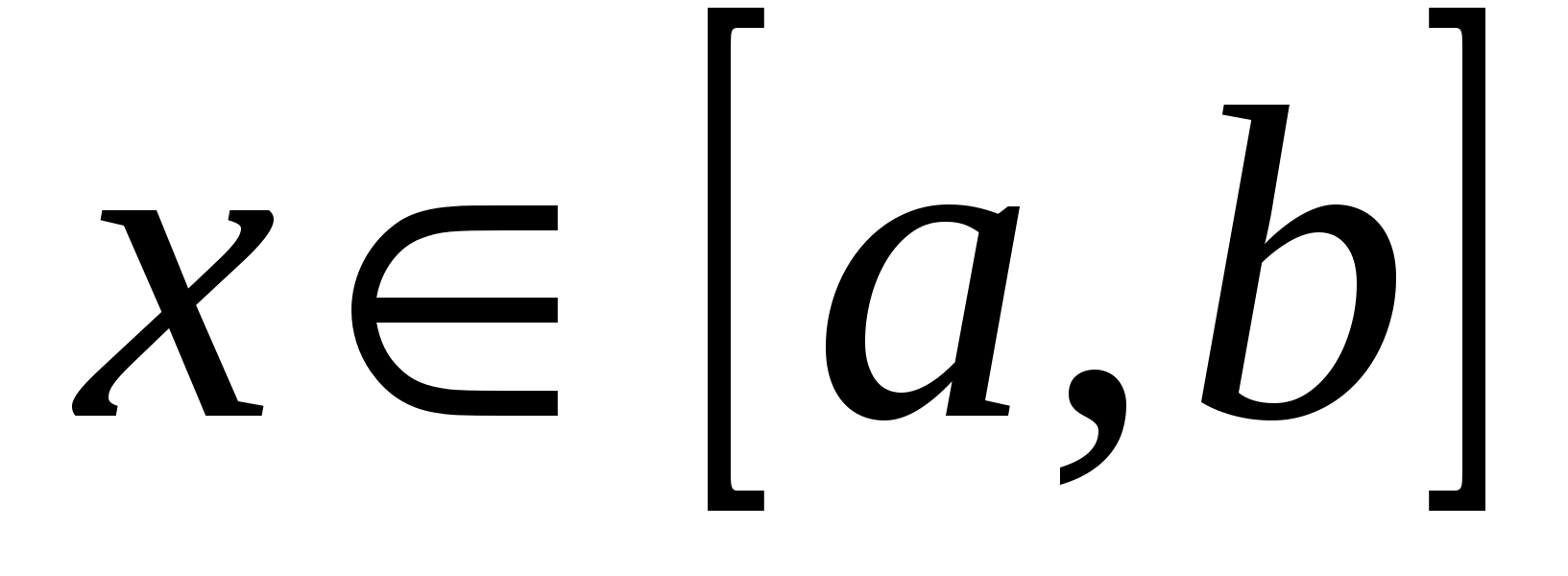 . Тогда получим
. Тогда получим
 . Это означает, что функция
. Это означает, что функция 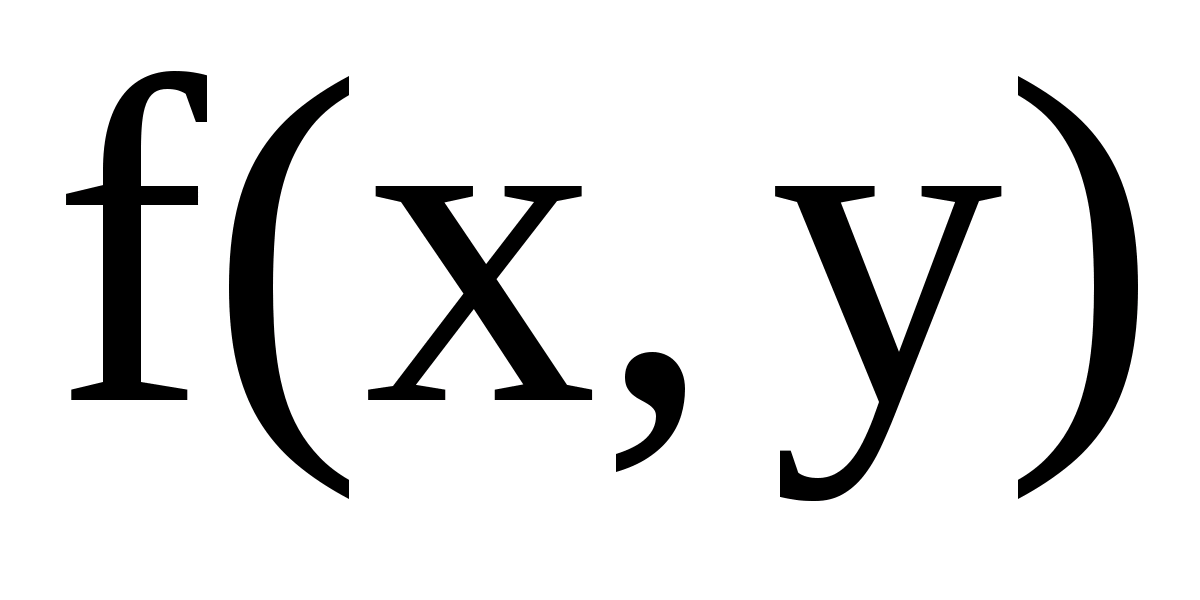 равномерно стремится к . В таком случае по теореме 3
равномерно стремится к . В таком случае по теореме 3  , а уже отсюда следует равенство
, а уже отсюда следует равенство  , то есть наша функция
, то есть наша функция 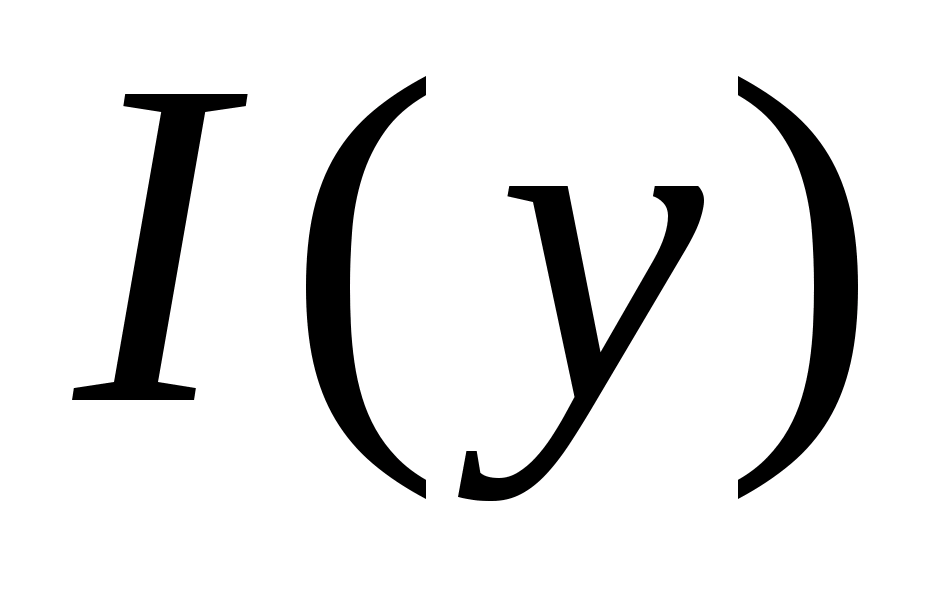 непрерывна на
непрерывна на  .
.
Замечание 4. Совершенно аналогично доказывается теорема для 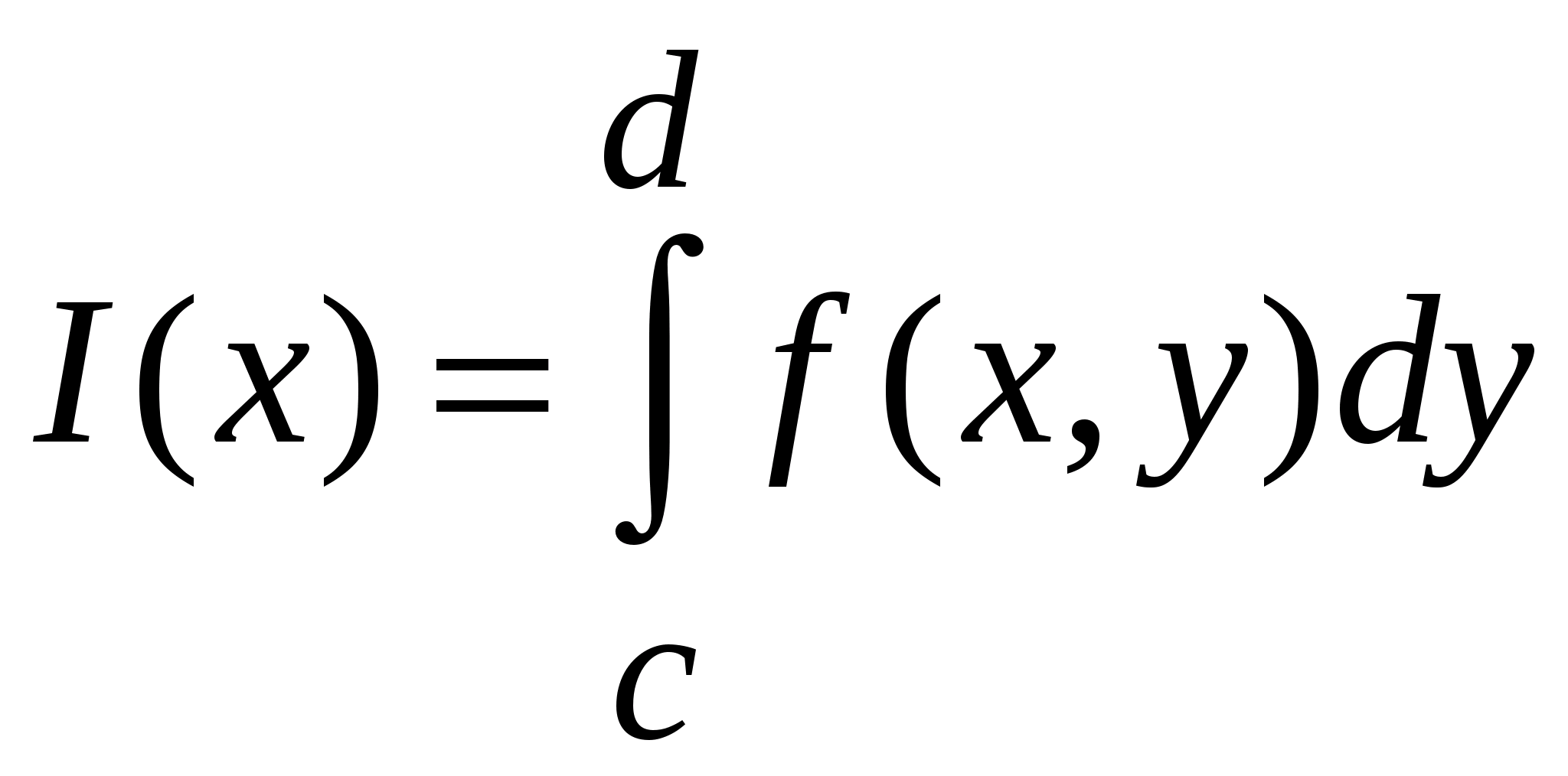 , где
, где 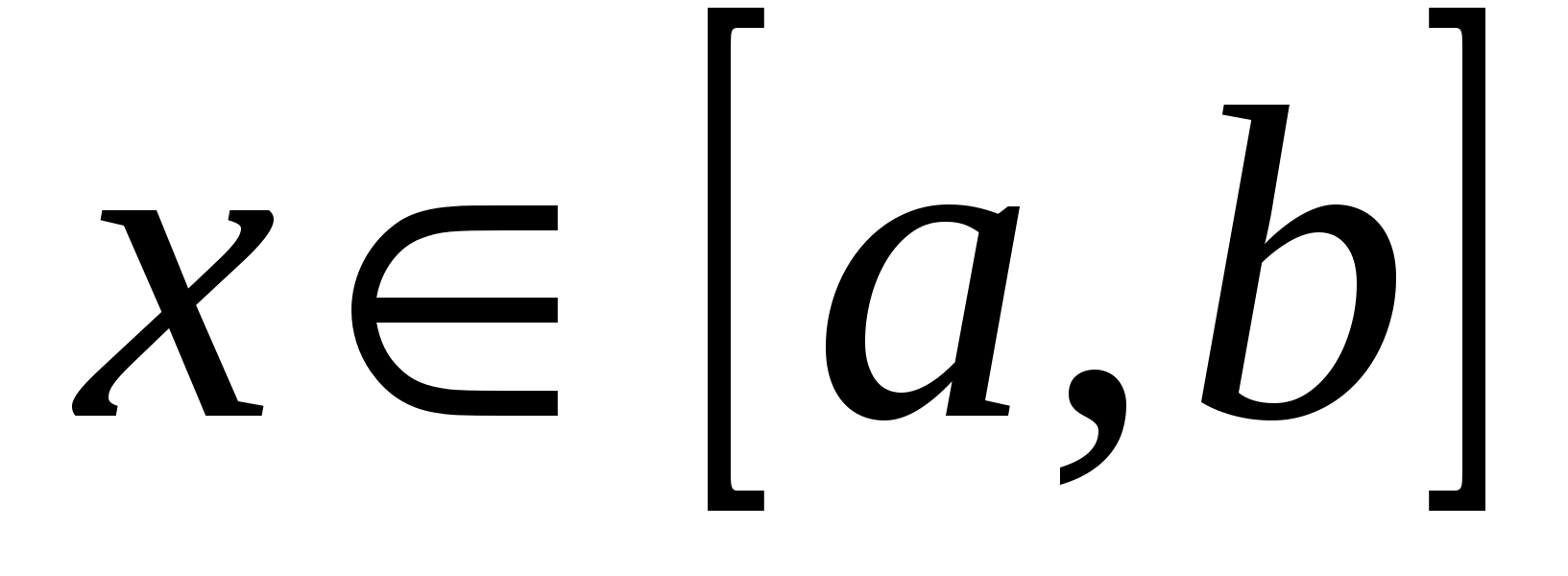 .
.
Следствие 2. Если 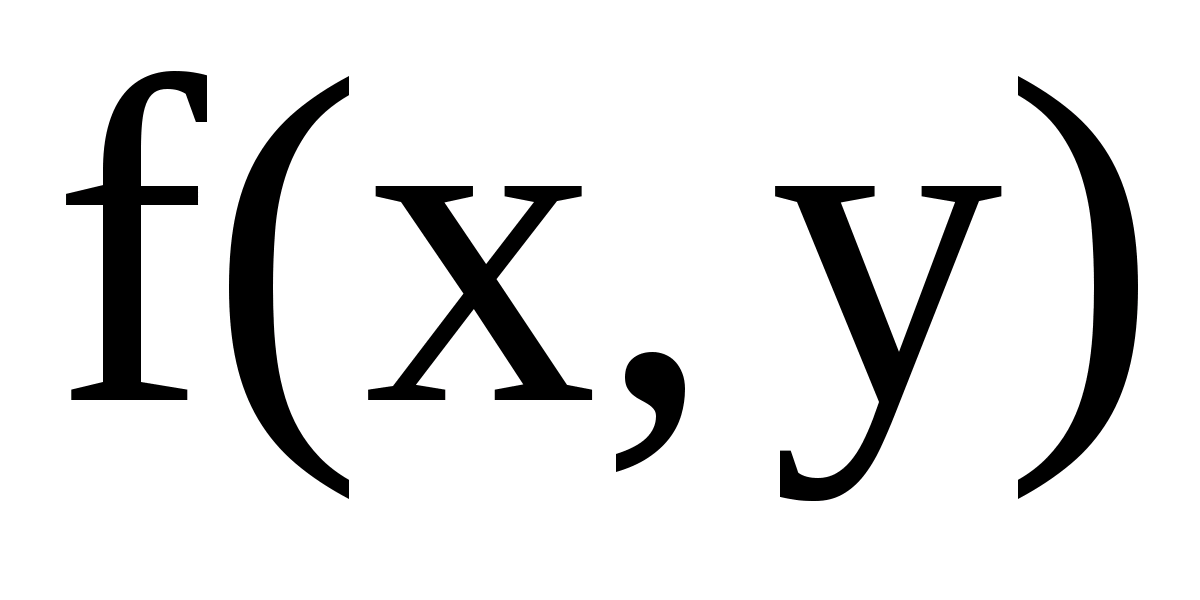 непрерывна на прямоугольнике
непрерывна на прямоугольнике  , то
, то  .
.
26 Задачи приводящие к понятиям кратного интеграла, криволинейного и поверхностного интеграла 1-го рода.
Пусть  – брус (промежуток) в
– брус (промежуток) в  ,
,  – разбиение промежутка I. На каждом из промежутков разбиения
– разбиение промежутка I. На каждом из промежутков разбиения  отметим точку
отметим точку  .
.
Получим  разбиение с отмеченными точками для
разбиение с отмеченными точками для  .
.
Величина  называется интегральной суммой Римана для функции f (x) на промежутке I по разбиению с отмеченными точками
называется интегральной суммой Римана для функции f (x) на промежутке I по разбиению с отмеченными точками  .
.
Def: 
 =
=  =
=  .
.
Обозначая  – множество функций интегрируемых на брусе I запишем:
– множество функций интегрируемых на брусе I запишем:
Def: 
 ε > 0
ε > 0  δ > 0
δ > 0  <
<  .
.
Если для функции f (x) на I и разбиения  – обозначить через
– обозначить через  – наибольшее и наименьшее значение функции f (x) на Ik то величины
– наибольшее и наименьшее значение функции f (x) на Ik то величины  =
=  и
и  =
=  называются нижней и верхней суммами Дарбу.
называются нижней и верхней суммами Дарбу.
Т0. Чтобы функция  была интегрируема на брусе
была интегрируема на брусе  (т.е.
(т.е.  ) необходимо и достаточно, чтобы
) необходимо и достаточно, чтобы 

 . Δ▲.
. Δ▲.
Определено интегрирование функции по брусу в евклидовом пространстве. А как функцию проинтегрировать по произвольному ограниченному множеству из евклидового пространства?
Определим интеграл от функции f по множеству  .
.
Def: Пусть 
 и
и  – ограничено, т.е.
– ограничено, т.е.  . Функцию
. Функцию  назовём характеристической функцией множества M .
назовём характеристической функцией множества M .
Тогда:  ≡
≡  .
.
Определение интеграла по множеству не зависит от того, какой брус, содержащий М выбран, т.е. 

 .
.
Это обозначает, что определение интеграла по множеству корректно.
Необходимое условие интегрируемости.Чтобы функция f (x) на М была интегрируемой необходимо, чтобы f (x) была ограниченной на М. Δ▲.
