Развертывая выражение m-й степени разности под знаком интеграла, получим сумму табличных интегралов.
Интеграл от четной положительной степени синуса и косинуса.
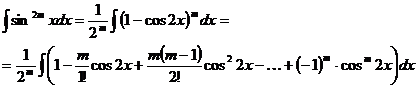
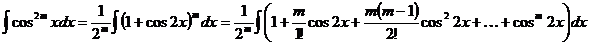
Применяя в обоих случаях почленное интегрирование, получим конечное число интегралов от четных и от нечетных степеней cos2x. В случае четной степени, снова воспользуемся формулой тригонометрии 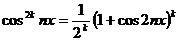 (формулой удвоения аргумента), а в случае нечетной степени применим прием 1). Через конечное число шагов придем к сумме табличных интегралов.
(формулой удвоения аргумента), а в случае нечетной степени применим прием 1). Через конечное число шагов придем к сумме табличных интегралов.
3) Интеграл от произведения целых положительных степеней синуса я косинуса. Приемы интегрирования целой положительной степени синуса и косинуса, изложенные в пунктах 1) и 2), достаточны для интегрирования произведений таких степеней, как это следует из приводимых ниже примеров.
Интеграл от нечетной положительной степени секанса и косеканса.
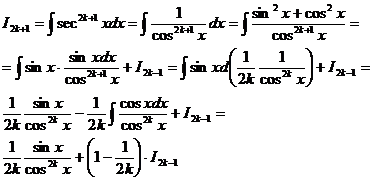
Значит
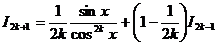
Получена рекуррентная формула. Последовательно применяя эту формулу, получим выражение 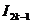 через
через 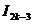 ,
, 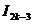 — через
— через 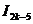 и т. д.; наконец,
и т. д.; наконец, 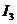 — через
— через 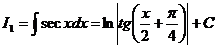 . Используя теперь полученные нами выражения в обратном порядке, найдем
. Используя теперь полученные нами выражения в обратном порядке, найдем  .
.
Интеграл от четной положительной степени секанса и косеканса.
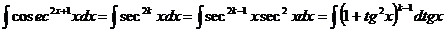 ..
..
Развернув (k— 1)-ю степень двучлена l + tg2x, придем к сумме табличных интегралов.
Универсальная тригонометрическая подстановка.
1. Общий случай. Пусть требуется вычислить интеграл вида 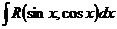 , подинтегральная функция которого является рациональной функцией от sin х и cos х. Применим подстановку
, подинтегральная функция которого является рациональной функцией от sin х и cos х. Применим подстановку 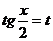 .(7.17)
.(7.17)
Тогда х = 2 arctg t, dx = 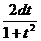 ; sin x = 2 sin
; sin x = 2 sin 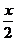 cos
cos 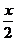 =
=
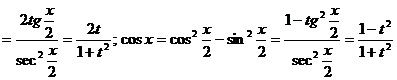 ;'следовательно,
;'следовательно,
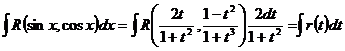 , где r{t) – рациональная функция аргумента t. Таким образом, с помощью подстановки (7.17) всякий интеграл вида
, где r{t) – рациональная функция аргумента t. Таким образом, с помощью подстановки (7.17) всякий интеграл вида 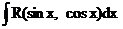 преобразуется в интеграл
преобразуется в интеграл 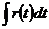 от рациональной функции, т. е. вычисляется в элементарных функциях.
от рациональной функции, т. е. вычисляется в элементарных функциях.
Интегрирование некоторых иррациональностей.
1. Вычисление интегралов вида 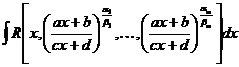 , где R —символ рациональной зависимости. Подинтегральная функция здесь является рациональной функцией от аргумента х и нескольких дробных степеней одной и той же дробно-линейной функции этого аргумента х. Применим подстановку:
, где R —символ рациональной зависимости. Подинтегральная функция здесь является рациональной функцией от аргумента х и нескольких дробных степеней одной и той же дробно-линейной функции этого аргумента х. Применим подстановку: 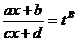 , (7.21) где В — общее наименьшее кратное чисел
, (7.21) где В — общее наименьшее кратное чисел 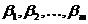 .
.
Покажем, что эта подстановка приводит все подинтегральное выражение к рациональному виду.
Из равенства (7.21) х выражается рационально через t; обозначим его так: 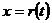 . Тогда
. Тогда 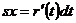 , где r'(t) есть рациональная функция t, как производная от рациональной функции r(t).
, где r'(t) есть рациональная функция t, как производная от рациональной функции r(t).
Далее
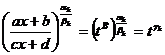 , где
, где 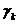 — целое число, поскольку В делится без остатка на каждое из чисел
— целое число, поскольку В делится без остатка на каждое из чисел 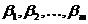 . Имеем
. Имеем 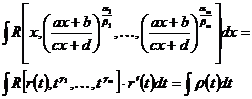
Где 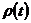 есть рациональная функция аргумента t.
есть рациональная функция аргумента t.
2. Вычисление интегралов от рациональной функции аргумента х и квадратного радикала из квадратного двучлена:
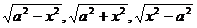 .
.
Вычисление таких интегралов производится с помощью соответствующей тригонометрических подстановок;
1) 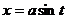 (17.22) в случае интеграла
(17.22) в случае интеграла 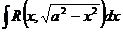 ;
;
2) 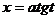 (17.23) в случае интеграла
(17.23) в случае интеграла 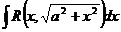
3) 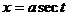 (17.24) в случае интеграла
(17.24) в случае интеграла 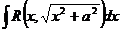 ..
..
Во всех трех случаях подрадикальное выражение превращается в точный квадрат, радикал исчезает, а интеграл получает вид 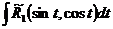 .
.
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ.
