РАСЧЁТНО-ГРАФИЧЕСКАЯ РАБОТА № 3

Принцип возможных перемещений

Задание: Используя принцип возможных перемещений совместно с принципом освобождения твёрдых тел от связей, определить реакции опор А, В, С, D для системысочленённых балок и определить значение силы F для механической системы с одной степенью свободы. Исходные данные приведены в таблице №4 и на схемах рис.4.

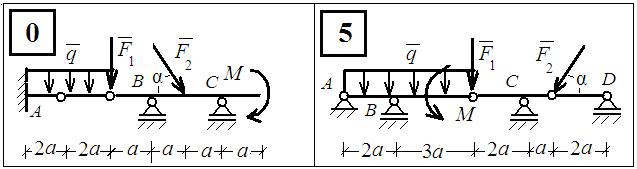
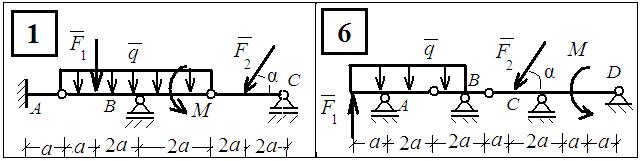
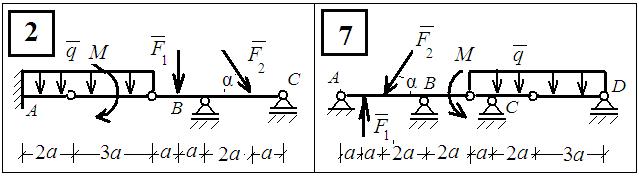
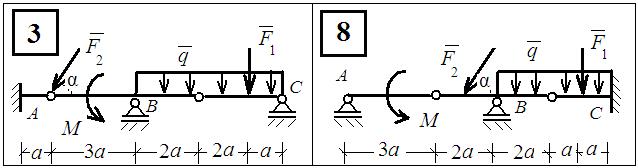
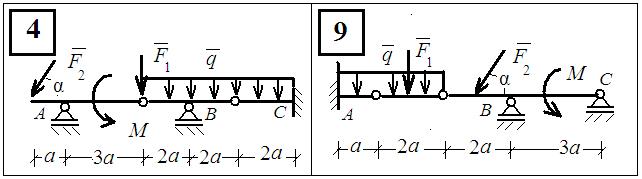
Рис.4

Последовательность расчёта:

1. Вычерчертить схему заданной механической системы с указанием

всех сил, действующих на неё.

2. Для удобства расчётов заменить действие равномерно - распределённой нагрузки сосредоточенной силой, приложенной в центре её тяжести: Q = q ∙ a.

3. На основании принципа освобождения твёрдых тел от связей, удалить искомую связь, заменяя её реакцией. Полученная таким образом система имеет одну степень свободы и допускает перемещения.

4. Показать схему возможных перемещений.

5. Составить уравнение работ всех сил на возможных перемещениях, учитывая, что действие связей заменено реакцией этой связи. На основании принципа возможных перемещений для равновесия механической системы с голономными идеальными, стационарными и двусторонними связями (таковыми являются все системы, приведённые в задании), необходимо и достаточно, чтобы сумма элементарных работ всех заданных сил и реакций связей, приложенных к точкам системы, была равна нулю на любом возможном перемещении системы:

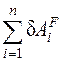= 0 или 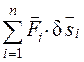= 0.

6. Используя подобие треугольников, установить зависимость

между перемещениями и решаем уравнение работ. Определить

искомую реакцию.

Таблица №3

Пер- вая цифра шифра	F1 кН	а   м	Вторая цифра шифра	αо	F2 кН	Третья цифра шифра № схемы	M   кН∙м	q   кН/м
		0,6
		0,4
		0,8
		0,3
		0,5
		0,3
		0,5
		0,7
		0,6
		0,8

Пример расчёта

Для составной балки (рис.а), на которую действуют силы, указанные на схеме, определить реакции опор А, С и Е.

• Заменяем равномерно - распределённую нагрузку сосредоточенной силой Q = q ∙ a = 1 ∙ 2 = 2 кН.

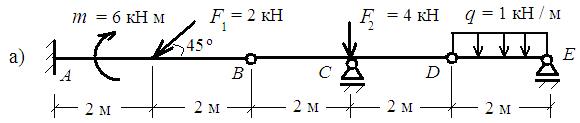
• Определяем реакцию опоры Е. (рис. б).

Отбрасываем опору Е, заменяя её реакцией R_E. Балка DE повернётся вокруг цилиндрического шарнира D на бесконечно малый угол δφ₁. Все остальные точки не имеют возможных перемещений.

Чертим схему возможных перемещений.

Из подобия треугольников: δs_q = 0,5 ∙ δs_E;

Составляем уравнение работ и решаем его, определяя искомую реакцию: 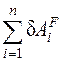= R_E ∙ δs_E – Q ∙ δs_q = 0; R_E ∙ δs_E = 2 ∙ 0,5δs_Е; R_E = 1кН

• Аналогично определяем реакцию опоры С. (рис. в).

Опору С заменяем реакцией R_С. Балка DE повернётся на бесконечно малый угол δφ₃ вокруг цилиндрического шарнира Е, а балка BD - вокруг шарнира В на угол δφ₂. Все остальные точки не имеют возможных перемещений. Чертим схему возможных перемещений.

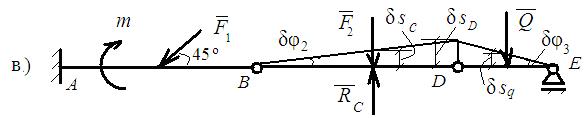
Из подобия треугольников: δs_q = δs_С = 0,5 ∙ δs_D ;

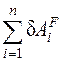= 0; R_С ∙ δs_С – F₂ ∙ δs_С - Q ∙ δs_q = 0;

R_С ∙ 0,5 ∙ δs_D – 4 ∙ 0,5 ∙ δs_D – 2 ∙ 0,5 ∙ δs_D = 0; R_C = 6 кН;

• Определяем горизонтальную составляющую реакции опоры А

(рис. г). Для этого заменяем жёсткое защемление опорой в виде ползуна, жёстко скреплённого с балкой. Такая опора позволяет исключить горизонтальную связь опоры А, которая компенсируется реакцией Х_А, но не допускает вертикальное перемещение и поворот. В этом случае система получает одну степень свободы.

А возможные перемещения будут только горизонтальными, одинаковыми для всех тел – δs.

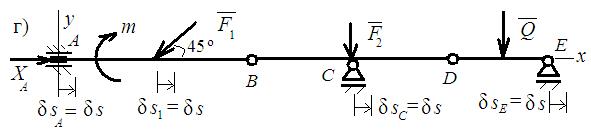
Уравнение работ получает вид: 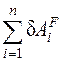= 0 ;

Х_А ∙ δs – F₁ ∙ cos45^o ∙ δs = 0; X_A – 2 ∙ 0,707 = 0; Х_А = 1,414 кН;

• Определяем вертикальную составляющую реакции опоры А (рис. д).

Для этого ползун располагаем вертикально, и вертикальная связь компенсируется вертикальной реакцией Y_А (по аналогии с предыдущей горизонтальной связью).

При сообщении системе возможных перемещений балка АВ получит поступательное вертикальное перемещение, балка ВD повернётся вокруг цилиндрического шарнира С, а балка DЕ - вокруг шарнира Е.

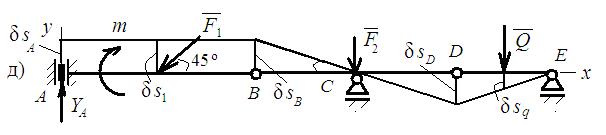
Из подобия треугольников: δs_А = δs₁ = δs_B =δs_D ; δs_q = 0,5 ∙ δs_D ;

Уравнение работ получает вид: 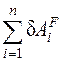= 0;

Y_А ∙ δs_А – F₁ ∙ sin 45^o ∙ δs₁ + Q ∙ δs_q = 0; Y_A – 2 ∙ 0,707 + 2 ∙ 0,5 = 0;

Y_А = 0,414 кН;

• Определяем реактивный момент опоры А. Для этого заменяем жёсткое защемление шарнирно-неподвижной опорой, а отброшенную связь – реактивным моментом М_А. (рис. е).

Даём системе возможные перемещения и определяем зависимости между ними.

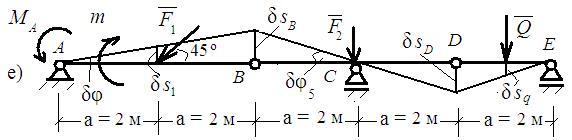
δs_B = δs_D = δs = 2а ∙ δφ = 4 ∙ δφ; δs_q = δs₁ =0,5 ∙ δs = 2 ∙ δφ;

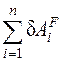= 0; М_А ∙δφ – m ∙ δφ – F₁ ∙ sin 45^o ∙ δs₁ + Q ∙ δs_q = 0;

М_А ∙ δφ – 6 ∙ δφ – 2 ∙ 0.707 ∙ 2 ∙ δφ + 2 ∙ 2 ∙ δφ = 0; М_А = 4,824кН∙м;

ПРИЛОЖЕНИЕ

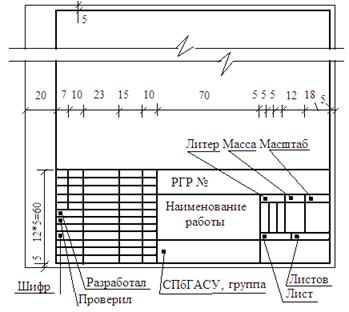
Образец оформления первого листа расчета

(формат листа А-4)

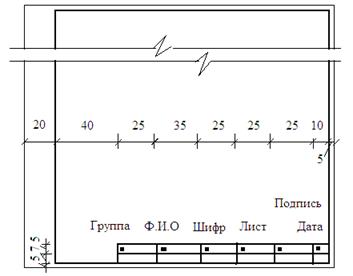
Образец оформления последующих листов расчета

(формат листа А-4)

Содержание

РГР № 1. Равновесие плоской системы связанных тел ……… 4

РГР № 2. Теорема об изменении кинетической энергии ……….. 7

РГР № 3. Принцип возможных перемещений для определения реакций опор в шарнирной балке ………………………………………15

ПРИЛОЖЕНИЕ…………………………………………………… 20

Масленников Никита Александрович

Теоретическая механика.

Сборник заданий

для расчетно-графических работ

Методические указания