Бросают два игральных кубика. Какова вероятность того, что выпадут две четные цифры?
+ А. 0,25;
В. 0,4;
С. 0,125.
Какова вероятность, что при одном броске игрального кубика выпадает число очков, равное четному числу?
А. 1/6;
В. 0,4;
+ С. 0,5.
54. Катя и Аня пишут диктант. Вероятность того, что Катя допустит ошибку, составляет 60%, а вероятность ошибки у Ани составляет 40%. Найти вероятность того, что обе девочки напишут диктант без ошибок.
А. 0,25;
+ В. 0,4;
С. 0,24.
55. Завод выпускает 15% продукции высшего сорта, 25% - первого сорта, 40% - второго сорта, а все остальное – брак. Найти вероятность того, что выбранное изделие не будет бракованным.
+ А. 0,8;
В. 0,1;
С. 0,015.
Какова вероятность, что ребенок родится 7 числа?
А. 7/30;
В. 7/12;
С. 7/31;
+ D. 7/365.
57. Каждый из трех стрелков стреляет в мишень по одному разу, причем попадания первого стрелка составляет 90%, второго – 80%, третьего – 70%. Найдите вероятность того, что все три стрелка попадут в мишень?
+ А. 0,504;
В. 0,006;
С. 0,5;
D. 0,3
В ящике 7 белых и 9 черных шаров. Наудачу вынимают шар и возвращают. Затем снова вынимают шарик. Какова вероятность, что оба шара белые
А. 25/49.
+ В. 49/256.
С. 16/489.
Какова вероятность появления хотя бы одного герба при подбрасывании двух монет?
А. 1/4.
В. 1/2.
+С. 3/4.
В инструментальном ящике находятся 15 стандартных и 5 бракованных деталей. Из ящика наугад вынимают одну деталь. Найти вероятность того, что эта деталь стандартна
+ А. 3/4.
В. 7/8.
С. 1/4.
В приборе имеются три независимо установленных сигнализатора об аварии. Вероятность того, что в случае аварии сработает первый равна 0.9, второй - 0.7, третий - 0.8. Найдите вероятность того, что при аварии не сработает ни один сигнализатор
А. 0.0006.
+ В. 0.006.
С. 0,504.
62. Николай и Леонид выполняют контрольную работу. Вероятность ошибки при вычислениях у Николая составляет 70%, а у Леонида – 30%. Найдите вероятность того, что Леонид допустит ошибку, а Николай нет.
А. 0,21
В. 0,49
С. 0,5
+ D. 0,09
63. Музыкальная школа проводит набор учащихся. Вероятность быть не зачисленным во время проверки музыкального слуха составляет 40%, а чувство ритма – 10%. Какова вероятность положительного тестирования?
+ А. 0,5
В. 0,4
С. 0,6
D. 0,04
64. Каждый из трех стрелков стреляет в мишень по одному разу, причем вероятность попадания 1 стрелка составляет 80%, второго – 70%, третьего – 60%. Найдите вероятность того, что в мишень попадет только второй стрелок.
А. 0,336
В. 0,056
С. 0,224
+ D. 0,144
65. В корзине лежат фрукты, среди которых 30% бананов и 60% яблок. Какова вероятность того, что выбранный наугад фрукт будет бананом или яблоком?
+ А. 0,9
В. 0,5
С. 0,34
D. 0,18
В коробке лежат 4 голубых, 3 красных, 9 зеленых, 6 желтых шариков. Какова вероятность того, что выбранный шарик будет не зеленым?
+ А. 13/22
В. 0,5
С. 10/22
D. 15/22
В лотерее 1000 билетов, среди которых 20 выигрышных. Приобретается один билет. Какова вероятность того, что этот билет невыигрышный?
А. 1/50
В. 0,2
+ С. 0,98
D. 0,09
68. Имеется 6 учебников, из которых 3 в переплете. Наудачу берут 2 учебника. Вероятность того, что оба взятых учебника окажутся в переплете составляет… .
+A. 0,2
B. 0,3
C. 0,5
D. 0,4
69. В цехе работают 7 мужчин и 3 женщины. По табельным номерам наудачу выбирают 3-х человек. Вероятность того, что все отобранные будут мужчинами составит … .
A. 0,3
B. 3/7
+ C. 0,292
D. 0,4
70. В ящике 10 шаров, из которых 6 окрашенных. Наудачу извлекают 4 шара, не возвращая их. Вероятность того, что все вынутые шары окажутся окрашенными, составляет… .
A. 0,6
+ B. 0,071
C. 0,142
71. В ящике 4 красных и 2 синих шара. Из него наудачу берут три шара. Вероятность того, что все эти три шара – красные, равна… .
A. 0,2
+ B. 0,75
C. 0,3
D. 0,4
72. Студент знает 20 вопросов из 25 вопросов по дисциплине. Ему предлагают 3 вопроса. Вероятность того, что студент знает их, составляет… .
A. 0,9
B. 0,8
+ C. 0,495
73. В урне 4 белых и 3 черных шара. Одновременно вынимают два шара. Вероятность того, что оба шара белые, составляет… .
+A. 4/7
B. 1/2
C. 2/7
74. Бросают 3 кубика сразу. Вероятность того, что выпадут 3 шестерки, составляет… .
+ A. 1/6
B. 1/36
C. 1/216
Участковый врач в течение недели принял 35 пациентов, из которых пяти пациентам был поставлен диагноз – язва желудка. Определите относительную частоту появления на приеме пациента с заболеванием желудка.
A. 0,02;
+ B. 0,7;
C. 1/7.
76. События А и В противоположные, если Р(А) = 0,4, тогда Р(В) = ...
А. 0,4;
В. 0,6;
С. 1;
+ D. верного ответа нет.
77. Если события А и В несовместимые и Р(А) = 0,2 а Р(В) = 0,05, то Р(А + В) =...
+ А. 0,25;
В. 0,1;
С. 1;
D. 0,15.
78. Если Р(В/А) = Р(В), то события А и В:
А. достоверные;
+ В. противоположные;
С. зависимые;
D. верного ответа нет
79. Условная вероятность события А при условии записывается в виде:
А.
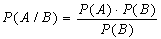 |
В
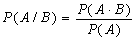 |
С
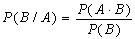 |
+ D
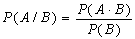 |
80. Если Р(АВ) = 0,35 и Р(В) = 0,7, то Р(А/В) = ...
А. 0,35;
В. 0,7;
+ С. 0,5.
81. Если вероятность события А не зависит от того, произошло ли событие В или нет, то Р(А) и Р(В) являются:
+ А. безусловными;
В. условными;
С. верного ответа нет
