Основные показатели количественной оценки риска

Математическое ожидание– среднее ожидаемое значение анализируемого показателя, взвешенное по вероятности получения результата по каждому из наблюдений:

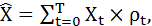где

T – период времени (или общее количество наблюдений);

t – номер периода времени (или наблюдения) по порядку;

X_t – единичное наблюдение (значение выбранного для анализа показателя);

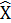– среднее ожидаемое значение наблюдения в их T совокупности;

r_t – вероятность получения результата (показателя) X_t.

Среднее линейное отклонениехарактеризует среднеарифметическое отклонение (по модулю) анализируемого показателя от его средней величины:

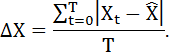
Здесь и далее возможны два варианта установления величины X_t:

· математическое ожидание (предпочтительно);

· арифметическое среднее значение.

Дисперсия - среднее арифметическое значение квадрата отклонения наблюдаемой величины от ее среднего значения:

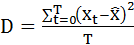, где

D – дисперсия;

Стандартное отклонение (среднеквадратическое отклонение) представляет собой квадратный корень дисперсии анализируемого показателя, собственно, величину (±) отклонения анализируемого показателя от его среднего значения:

.

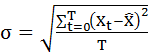Со стандартным отклонением связано правило «трех сигма»: в нормально распределенной совокупности все значения анализируемого показателя, выходящие за границы

,

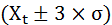полагаются нетипичными (резко выделяющимися) и не учитываются при анализе общей тенденции изменения показателя.

Коэффициент вариации анализируемого показателя характеризует относительную меру изменения показателя относительно его среднего значения:

.

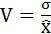Показатель можно выражать в процентах, что облегчает его понимание. Он характеризует однородность данных. Установлена следующая шкала оценки значений коэффициента вариации, выраженного в процентах [6]:

· до 10% - слабая колеблемость значений;

· 10-25% - умеренная колеблемость значений;

· Свыше 25% - высокая колеблемость значений.

Размах вариации характеризует разницу между максимальным и минимальным значением показателя:

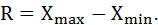
Все эти показатели ориентированы на оценку изменения анализируемого показателя как в положительную («хорошую» для инвестора), так и в отрицательную («плохую» для инвестора) сторону. К примеру, если инвестор согласен на доход 10% на вложенный капитал, ему же сообщили, что в результате наличия неопределенности он получит отдачу в диапазоне 10-50%, его суждение об эффективности проекта только улучшится. Хотя налицо риск изменения ожидаемого результата (но только в «хорошую» для инвестора сторону). Математически риск будет иметь место, фактически – нет.

Поэтому простой анализ предыдущих показателей необязательно даст «справедливую» оценку инвестиционного проекта для инвестора.

Вполне очевидно, что в одних случаях рискованным является любое отклонение от расчетного результата. Например,

· низкая урожайность имеет последствием рост цен, но «нечего» продать, тогда доходы уменьшатся. Наоборот, высокая урожайность в регионе в качестве последствия будет иметь снижение цен, тогда доходы вновь могут уменьшиться из-за собственно падения цен. Здесь все приведенные показатели будут эффективны в анализе без дополнительных вычислений;

· изменение доходности проекта в диапазоне, изначально удовлетворяющем требованиям инвестора (на уровне заведомо выше требуемой нормы доходности) не будет восприниматься рискованным, поскольку в любом случае устраивает инвестора. Тогда приведенные выше показатели будут давать завышенную оценку риска.

В первом примере для инвестора рискованным будет любое отклонение от ожидаемого значения, во втором – только отклонение в отрицательную от ожидаемого значения сторону.

Для оценки риска ухудшения ситуации возможно использование показателя вероятности попадания в неблагоприятный интервал:

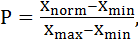где

X_norm – нормативное (расчетное) значение показателя;

X_min – минимальное значение в обследованной совокупности;

X_max – максимальное значение в обследованной совокупности.

В случае расчета этого показателя в качестве рискованного учитывается только отклонение показателя в худшую от норматива сторону.

После учета рисков и их количественной оценки используются следующие методы оценки эффективности проектов с учетом риска:

· метод корректировки нормы дисконта (метод оценки требуемой нормы доходности);

· метод достоверных эквивалентов;

· метод сценариев;

· анализ устойчивости (предельных параметров) и чувствительности проекта;

· «дерево решений»;

· Метод Монте-Карло (имитационного моделирования) и другие.

Метод корректировки нормы дисконта предполагает установление требуемой нормы доходности как суммы безрисковой ставки процента и премии за риск. Главное преимущество – простота. Главный недостаток – отсутствие учета степени риска, вероятностных характеристики стоимостных потоков.

Метод достоверных эквивалентов заключается в разработке «умеренно пессимистического» варианта инвестиционного проекта, в котором денежные потоки уточнены при помощи специальных поправочных коэффициентов, определяемых для каждого периода времени отдельно.

Например, в качестве поправочных коэффициентов могут быть использованы:

· ежегодный темп инфляции (индекс роста цен) с дифференциацией его уровня по годам и видам товаров;

· коэффициент паритета цен (неравномерность изменения цен по отраслям и товарам);

· коэффициент использования производственной мощности;

· коэффициенты для формирования страховых фондов (например, одно из условий сбалансированности бюджета – коэффициент покрытия ссудной задолженности не ниже 0,15, страховой фонд семян 15-20%, уровень непредвиденных затрат – 3-15%) и так далее.

Из всех проектов, разработанных таким способом, лучшим признается тот, который показывает максимум критерия NPV или другого показателя эффективности. Главное преимущество – разработка только одного варианта проекта. Главный недостаток – имеется опасность ошибки учета риска в расчетах.

Метод сценариев заключается в разработке не менее трех вариантов проекта («худший», «средний», «лучший»), учитывающих возможные изменения условий его реализации в будущем. Проект считаестя эффективным и малорискованным, если во всех вариантах его эффективность подтверждается.

Алгоритм анализа отдельного проекта методом сценариев:

1) определяются возможные варианты развития проекта: пессимистический («худший»), наиболее вероятный или базовый сценарий («средний»), оптимистический («лучший»);

2) по каждому варианту устанавливается его вероятностная характеристика (объективная – метод аналогов или статистический, субъективная – экспертный метод);

3) по каждому варианту рассчитываются показатели эффективности (например, NPV);

4) во всей совокупности вариантов для выбранного показателя эффективности вычисляется его среднее значение;

5) вычисляется среднеквадратическое отклонение показателя;

6) вычисляется коэффициент вариации;

7) формируется вывод о степени риска проекта.

Если во всех вариантах развития ситуации показатели эффективности проекта подтверждают его целесообразность, он признается устойчивым.

При разработке сценариев наиболее часто учитываются:

а) изменение цен на сырье,

б) изменение цен на продукт,

в) изменение ставок процента, учесть в норме дисконта поправку на риск.

г) появление или увеличение непредвиденных затрат,

д) увеличение стоимости строящихся объектов.

При отсутствии информации о возможных, с точки зрения участника проекта, пределах изменения значений указанных параметров официальной методикой 1999 г. рекомендуется провести вариантные расчеты реализуемости и эффективности проекта последовательно для следующих сценариев:

1) увеличение инвестиций. При этом стоимость работ, выполняемых российскими подрядчиками, и стоимость оборудования российской поставки увеличиваются на 20%, стоимость работ и оборудования инофирм - на 10%. Соответственно изменяются стоимость основных фондов и размеры амортизации в себестоимости;

2) увеличение на 20% от проектного уровня производственных издержек и на 30% удельных (на единицу продукции) прямых материальных затрат на производство и сбыт продукции. Соответственно изменяется стоимость запасов сырья, материалов, незавершенного производства и готовой продукции в составе оборотных средств;

3) уменьшение объема выручки до 80% ее проектного значения;

4) увеличение на 100% времени задержек платежей за продукцию, поставляемую без предоплаты;

5) увеличение процента за кредит на 40% его проектного значения по кредитам в рублях и на 20% по кредитам в СКВ.

Эти сценарии рекомендуется рассматривать на фоне неблагоприятного развития инфляции, задаваемой экспертно.

Главное преимущество – анализ проекта в широком диапазоне условий его реализации. Главный недостаток – высокая трудоемкость расчетов, небольшое количество наблюдений для расчета математических показателей риска.

Метод анализа устойчивости (предельных параметров) и чувствительности проектазаключается в изучении влияния отдельных факторов на его эффективность.

Метод построения «дерева решений»сходен с методом сценариев и основан на построении многовариантного прогноза динамики внешней среды. Предполагает возможность принятия самой организацией решений, изменяющих ход реализации ИП. Данный метод может применяться в ситуациях, когда более поздние решения сильно зависят от решений, принятых ранее, и в свою очередь, определяют сценарии дальнейшего развития событий.

Содержание метода:

1) период исполнения инвестиционного проекта условно делят на временные интервалы, исходя из представления, что каждый временной интервал начинается с особо значимого для общего проекта события, причем в этот момент существует ограниченный набор инвестиционных альтернатив;

2) для каждого периода определяют частную проблему и все возможные альтернативные варианты дальнейших событий;

3) формируют «дерево» за счет соответствующих проблем (вершин) и вариантов их решения (исходящих дуг);

4) для каждой дуги проводят ее денежную и вероятностную оценки;

5) за счет частных решений формируют путь решения конечной инвестиционной проблемы, получая фактически «дерево». Одновременно демонстрируют иные пути, которые могут возникать из-за наличия альтернатив при инвестировании;

6) исходя из значений, присвоенных вершинам и дугам, рассчитывают вероятное значение глобального критерия проекта (NPV, IRR, PI), а также глобальные критерии, характеризующие альтернативные направления ресурсных потоков, формирующихся при реализации данного инвестиционного направления.

Последовательность формирования «дерева решений»:

• определение состава и продолжительности фаз жизненного цикла проекта;

• определение ключевых событий, которые могут повлиять на дальнейшее развитие проекта;

• определение времени наступления ключевых событий;

• формулировка всех возможных решений, которые могут быть приняты в результате наступления каждого ключевого

события;

• определение вероятности принятия каждого решения;

• определение стоимости каждого этапа осуществления проекта (стоимости работ между ключевыми событиями) в текущих ценах.

Основными недостатками данного метода при его практическом использовании являются,

во-первых, техническая сложность данного метода при наличии больших размеров исследуемого «дерева» решений, так как затрудняется не только вычисление оптимального решения, но и определение данных,

во-вторых, присутствует слишком высокий субъективизм при назначении оценок вероятностей.

Метод имитационного моделирования (Метод Монте-Карло) заключается в формировании математической модели процесса и проведении комплекса циклических расчетов при подстановке в качестве исходных данных серии случайных чисел. В отличие от метода сценариев предполагает изучение всех вариантов изменения ключевых факторов проекта.

Алгоритм имитационного моделирования может быть представлен в виде последовательности шагов:

1. Формируется (или корректируется) модель обоснования проекта в виде набора бюджетов (в среде MS Excel, Project Expert и т.д.).

2. Модель рассматривается как черный ящик, система, на вход которой подаются исходные данные проекта (например, цена продукта, объем предполагаемых продаж, процентная ставка дисконтирования, ставка по кредитам, предполагаемый уровень инфляции и т. д.). В качестве результата на выходе черного ящика принимается только один параметр. Чаще всего им служит значение NPV.

3. Определяются ключевые факторы, влияющие на ИП, например, на основе анализа чувствительности проекта. Выбирается переменный параметр, для которого задается характер вероятности его значений в будущем и при необходимости фиксируются остальные факторы. В качестве его значений вводятся случайные числа с законом распределения, характерным для поведения этого фактора. Серии случайных чисел могут составлять последовательности, состоящие из нескольких тысяч и даже десятков тысяч значений, имитирующих изменение переменного параметра.

4. Выполняется анализ полученных данных, дается количественная оценка риска, составляется план управления фактором риска. Суждение об уровне риска и значимости изменения анализируемого фактора составляются на основе сопоставления параметров распределения результата и фактора.

Метод является достаточно трудоемким, предусматривает циклическое повторение одних и тех же вычислений по модели много тысяч раз в процессе подстановки в качестве исходных данных серии случайных чисел, из-за которых метод получил второе название метода Монте-Карло.

Метод Монте-Карло встречает серьезные препятствия в практическом применении, что обусловлено следующими основными причинами:

· высокая чувствительность получаемого результата по методу Монте-Карло к законам распределения вероятностей и видам зависимостей входных переменных инвестиционного проекта;

· современные программные средства позволяют обработать большое количество информации, однако получение качественной статистической информации не представляется возможным по самым различным причинам (временным, финансовым и т. д.), особенно для уникальных ИП в реальном секторе экономики;