Замена платежей и их консолидация

При замене параметров платежей или их консолидации (несколько платежей объединяются в один) формируется финансовый эквивалент, включающий суммы, приведенные к одному и тому же моменту времени. Он имеет форму:

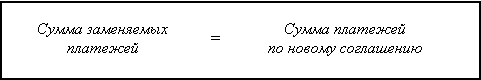
Поскольку финансовый эквивалент представляет собой одно равенство с несколькими параметрами, в частности, следует определить либо новую сумму платежей 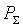, либо новый срок 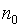платежа, то это равенство дисконтированных сумм:

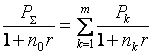(29)

при применении процентной ставки;

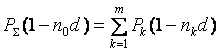(30)

при применении учётной ставки.

Если в новом соглашении положить 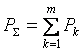, то новый срок определяется как

(31)

при применении процентной ставки;

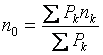(32)

при применении учётной ставки.

Для случая более простой ситуации, когда параметры одного платежа заменяются новыми значениями, можно рассуждать так:

а) при отдалении срока платежа наращиваются проценты:

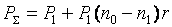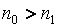, , (33)

при применении процентной ставки;

б) при сокращении срока платежа, т. е. 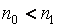, надо сумму 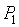математически дисконтировать на срок :

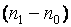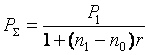. (34)

Сложные проценты

Наращение сложных процентов

Для поощрения долгосрочных вкладов клиентов применяют процедуру капитализации процентов, т. е. присоединение начисленных процентов к базе и в дальнейшем начисление процентов на эту сумму. Такая схема процентов называется схемой сложных процентов.

Наиболее простой вид алгоритма наращения по схеме сложных процентов получим, если в формуле (13) положим :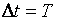

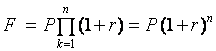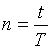, . (35)

В общем случае в формуле (35) число 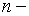положительное вещественное число (целое или дробное). Так, если 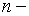целое число, то 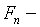наращенная сумма за 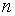годовых периодов при начальной сумме 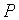ссуды при процентной ставке 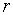. Множитель называется множителем наращения.

Поучаемые проценты

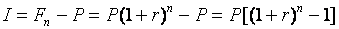. (36)

Если 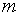периодов начисления с капитализацией процентов произвольны, но исчисляется каждый целым числом лет 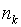и годовая ставка процентов 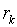переменная , то наращенная сумма

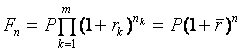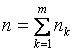, , (37)

.

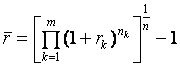Замечание.

Отвечая на вопрос «Чему равно 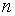, чтобы удвоить первоначальную сумму 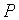, т. е. получить 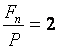?», получим:

 по схеме простых процентов ;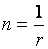

 по схеме сложных процентов .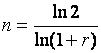

Смешанная схема процентов

Сравнение процессов наращения по схеме простых процентов со схемой сложных процентов показывает, что на временном интервале до 1 года наращенная сумма по схеме простых процентов оказывается больше. Отсюда вывод: кредитор применяет схему сложных процентов на интервалах более 1 года, а простую – на интервалах до 1 года.

Если 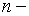нецелое число лет, то представим его в виде суммы целой и дробной частей:

.

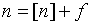Тогда исчисление наращенной суммы по формуле

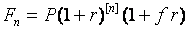(38)

называют смешанной схемойсложных процентов.