Консолидация и замена платежей

В реальной ситуации нередко одна из сторон коммерческой сделки обращается к другой с предложением изменить условия ранее заключенных соглашений.

Наиболее часто предлагается изменить сроки платежей в сторону их увеличения, произвести объединение нескольких платежей в один (консолидировать платежи) с установлением единого срока погашения.

Принцип, на котором базируется такое изменение контракта, называется принципом финансовой эквивалентности обязательств, который предполагает неизменность финансовых отношений сторон до и после изменения контракта.

Эквивалентнымисчитаются такие платежи, которые, будучи приведены к одному моменту времени, оказываются равными. Рассмотрим рис. 6 S₁ и S₂ - суммы, приуроченные к моменту времени t = 2 и t = 4 соответственно.

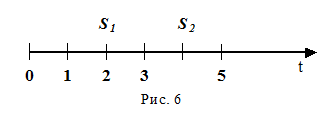
Приведем обе суммы S₁ и S₂ к начальному моменту времени по ставке приведения i, т.е. произведем дисконтирование этих сумм:

A₁ = S₁ (1 + i)^-2, A₂ = S₂ (1 + i)^-4.

Если A₁ = A₂ , то суммы S₁ и S₂ эквивалентны. Следовательно, замена суммы S₁ при t = 2 на сумму S₂ при t = 4 и наоборот, не изменит финансовых отношений сторон участников коммерческой сделки. Рассмотрим рис.7.

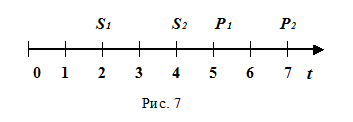
Здесь сравниваются два потока платежей: S₁ , S₂ и P₁, P₂ по сложной процентной ставке i. Для того чтобы заменить суммы S₁ и S₂ на две другие, эквивалентные по своим финансовым последствиям, суммы P₁ и P₂, применим принцип финансовой эквивалентности. Именно, приведем платежи S₁ и S₂ к начальному моменту времени (можно к любому другому) и сложим их:

S₁ (1 + i)^-2 + S₂ (1 + i)^-4 . (27)

То же самое проделаем с платежами P ₁ и P ₂:

P₁ (1 + i)^-5 + P₂ (1 + i)^-7. (28)

Приравнивая (27) и (28), получимуравнение эквивалентности:

S₁ (1 + i)^-2 + S₂ (1 + i)^-4 = P₁ (1 + i)^-5 + P₂ (1 + i)^-7. (29)

Очевидно, что данный метод распространяется на любое конечное число сумм. Если сравнение происходит по простой ставке i, то уравнение (29) примет вид:

S₁ (1 + 2i)^-1 + S₂ (1 + 4i)^-1 = P₁ (1 + 5i)^-1 + P₂ (1 + 7i)^-1.

В случае, когда несколько платежей S₁, S₂, S₃ со сроками n₁, n_2, n₃ соответственно, заменяются одним S₀ со сроком n₀, то уравнение эквивалентности в случае простых процентов запишется в виде:

S ₀ = S₁ (1 + (n₀ - n₁ )i) + S ₂ (1 + (n₀ - n₂ )i) + S₃ (1 + (n₀ - n₃ ) i),

если n ₀ > n₁, n₂, n₃. В другом случае, если n₁ < n₀ < n₃, нужно применять как наращение (при n₀ > n_k), так и дисконтирование (n₀ < n_k).

Если проценты сложные, то, если n₁ < n₀ < n₂ < n₃, уравнение эквивалентности примет вид (суммы приводятся к моменту n₀):

S₀ = S₁ (1 + i) 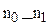+ S₂ (1 + i) 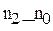^-( ) + S₃ (1 + i)^{-( )} .

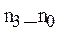Пример.Два платежа - 1 и 0,5 млн руб. со сроками уплаты соответственно 150 и 180 дней - объединяются в один со сроком 200 дней. Определите консолидированную сумму долга, если стороны согласились на применение простой ставки, равной 20 %.

Решение. Приводя суммы 1 и 0,5 млн руб. к сроку n₀ = 200 дней, получим уравнение эквивалентности (К = 360):

S₀ = 1000 (1 + 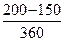0,2) + 500 (1 + 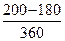0,2) = 1533,32 тыс. руб.

Пример.Имеется два кредитных обязательства - 500 тыс. руб. и 600 тыс. руб. со сроками уплаты 01.10 и 01.01 (нового года).

По согласованию сторон обязательства были пересмотрены на новые условия: первый платеж в размере 700 тыс. руб. должник вносит 01.02, остальной долг он выплачивает 01.04. Ставка сравнения 10 % простая. Рассчитайте величину второго платежа S₀.

Решение. За дату приведения примем 01.01 (нового года), К = 360. Учитывая, что 01.10 - 274-й порядковый день в году, 01.02 - 32-й день, 01.04 - 91-й день, запишем уравнение эквивалентности:

500 (1 + 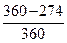0,1) + 600 = 700 (1 + 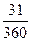0,1)^-1 + S ₀ (1 + 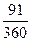0,1)^-1.

Решая это уравнение относительно S₀, находим: S₀ = 409,417 тыс. руб.

Задачи

7.1. Долг в размере 300 тыс. руб. должен быть выплачен через два года. Найдите эквивалентные значения для этой суммы (ставка сравнения 25 %):

а) в конце первого года,

б) через 5 лет.

Ответ: а) 240 тыс. руб.; б) 585,938 тыс. руб.

7.2.Вычислите эквивалентное значение долга, которого он достигнет через два года, если в настоящее время он составляет 42 тыс. руб. Проценты начисляются поквартально по ставке 40 % годовых. Ответ:90,031 тыс. руб.

7.3. Исходный поток платежей составляет: 200 тыс. руб. - через один год, 175 тыс. руб. - через два года, 210 тысяч руб. - через 4 года. Замените его эквивалентным множеством, состоящим из двух выплат, равных по величине, первая из которых осуществляется через 1,5 года, а вторая - через 4 года. Проценты начисляются по ставке 8 % годовых каждые полгода.

7.4.Долг должен быть погашен двумя платежами: 100 тыс. руб. через один год и 370 тыс. руб. через три года. Определите срок, при котором замена обеих выплат одной, в размере 480 тыс. руб., будет эквивалентной при ставке – 15 % годовых.

7.5. По условиям контракта, заключенного 01.02, за полученные в кредит товары фирма должна заплатить через 120 дней - 1,5 млн руб., а затем через 240 дней еще 1,2 млн руб. Достигнуто соглашение с кредитором об изменении условий контракта. Платежи производятся равными суммами: первый платеж - через 90 дней, второй - через 180 дней. При расчете применяется простая ставка 10 % годовых. Определите величину каждого платежа. Ответ: 1,3361 млн руб.

7.6.Строительная фирма получила в банке долгосрочный кредит в размере 5 млн. руб. под 6 % годовых (проценты сложные), срок погашения - через 5 лет. Впоследствии стороны пересмотрели условия займа и выработали новые: через три года производится выплата 3 млн. руб., остальная сумма выплачивается через 4 года. Процентная ставка сохраняется прежней. Определите сумму окончательного платежа.

7.7. Заемщик должен уплатить кредитору 10 млн руб. через 5 лет. Стороны согласились изменить условия погашения долга: через 2 года выплачивается 3 млн руб., а оставшийся долг спустя 4 года после первой выплаты. Определите сумму окончательного платежа, если сложная процентная ставка равна 10 % годовых.