Расчет структурных средних величин, абсолютных и относительных показателей вариации

Имеются следующие данные о величине чистой прибыли мелких предприятий по приведенным данным определим среднюю величину чистой прибыли, показатели моды и медианы, среднее линейное отклонение, среднеквадратичное отклонение, дисперсию, коэффициент ассицилляции, коэффициент вариации, относительное линейное отклонение. Дадим графическое изображение ряда в виде гистограммы и кумуляты.

Таблица 6

Исходная таблица

Величина чистой прибыли, тыс. руб.	20 -40	40 -60	60 -80	80 -100	100 -120
Число мелких фирм

Для поставленной задачи воспользуемся данными расчетами рабочей (расчетной) таблицей:

Таблица 7

Расчетная таблица

Величина чистой прибыли, тыс. руб, х	Число мелких фирм, f	Середина Интервала, Х´ = (хк +хн) / 2	Х´ * f	׀ Х´ - хср׀	׀ Х´ - хср׀ * f	(Х´ - хср)2	(Х´ - хср)2 * f
А
20 - 40				37, 98	455, 76	1442, 48	17309, 76
40 – 60				17, 98		323, 28
60 – 80				2, 02	191, 9	4, 08	387, 6
80 – 100				22, 02	616,56	484, 88	13576, 64
100 - 120				42, 02	546, 26	1765, 68	22953, 84
ИТОГО		-		-	2709, 48	4020, 4	70 391, 84

Прежде всего, находим середины интервалов (Х´) по исходным данным (гр. А) и записываем их в таблицу (гр. 2).

Определим произведения значений середин интервалов (Х´) на соответствующие им веса (f_i) (гр. 3). Рассчитаем среднюю величину по формуле арифметической взвешенной:

Хср = ∑(х_i * f_i) / ∑ f_i = 13460 / 198 = 67, 98 тыс. руб. на 1 фирму.

Для расчета среднего линейного отклонения находим абсолютной отклонения середины интервалов, принятых нами в качестве вариантов признака (Х´) от середины величины (Хср) (гр. 4). Поскольку сумма отклонений значений признака от средней величины равна нулю, приходится все отклонения брать по модулю, на что указывают прямые скобки в числители формул.

Наконец, вычисляем произведения отклонений ׀ Х´ - хср׀ на их веса (f_i) и подсчитаем сумму этих произведений. Эта сумма равна 2709, 48. Результаты записываем в гр. 5.

Среднее линейное отклонение (dср) определяется как средняя арифметическая:

dср = ∑ ׀ Х´ - хср* ׀ f_i / ∑f_i = 2709, 48 / 198 = 13, 6842

Таково в среднем отклонении вариантов признака от их средней величины. Это отклонение по сравнению со средней величиной признака малое. Оно отличается от средней на 54, 2958 тыс. руб. Это свидетельствует о том, что данная совокупность в отношении нашего признака однородная, а средняя – типична. Действительно, средняя величина выведена из величин, не резко отличающихся (например, максимально значение признака только в 3,67 раза больше минимального – 110 против 30).

Поэтому для точного колебания совокупности найдем дисперсию (σ²) и среднее квадратичное отклонение (σ),как корень квадратный из дисперсии.

σ² = ∑(Х´ - хср)² * f_i / ∑f_i =70 391, 84 / 198 = 355, 51 тыс. км.

σ = (∑(Х´ - хср)² * f_i / ∑f_i)^1/2 = (355, 51)^1/2 = 18, 85 тыс. км.

Степень вариации в данной совокупности невелика, так как средняя величина равна 67, 98 тыс. руб. Это говорит об однородности рассматриваемой нами совокупности.

Найдем коэффициент осцилляции (V_R):

V_R = R / хср * 100%

R – Размах вариации равный разности максимального признака и минимального признака = Х´мак - Х´мин = 120 – 20 = 100 тыс. км.

V_R = R / хср * 100% = 100 / 67, 98 * 100 % = 147, 1%.

Линейный коэффициент вариации (Vdср):

Vdср = dср / хср * 100% = 13, 6842 / 67, 98 * 100% = 20, 13%

Коэффициент вариации (Vσ):

Vσ = σ /хср * 100% = 18, 85/ 67, 98 * 100% = 27, 73 %

Совокупность считается однородной т. к. коэффициент вариации не превышает 33%.

Определим моду (Мо):

Мо = х₀ + i * (f_мо – f_мо-1) / ((f_мо – f_мо-1) + (f_мо – f_мо+1)),

Где х₀ – нижняя граница модально интервала (модальным интервалом называется интервал, имеющий наибольшую частоту – в нашем примере это интервал 60 -80);

i – величина модального интервала (20 тыс. руб.);

f_мо – частота модального интервала (95);

f_мо-1 – частота интервала, предшествующего модальному (50)

f_мо+1 – частота интервала, следующего за модальным (28).

Мо = 60 + 20* ((95 – 50) / (95 – 28)) = 73, 43 тыс. руб.

73, 43 тыс. руб. величина чистой прибыли приходится на самое большое количество фирм 95 шт.

Найдем медиану (Ме):

Ме = х₀ + i * (1/2 * ∑f_i – S_{Ме – 1}) / f_ме,

Где х₀ – нижняя граница медианного интервала (медианным интервалом называется первый интервал, накопленная частота которого превышает половину общей суммы частот – в нашем примере половина общей суммы равна 198 / 2 = 99, это интервал 60 -80 т. к. накопленная частота его равна 12 + 50 + 95 = 157);

i – величина медианного интервала (20 тыс. км.)

S_{Ме – 1} – накопленная частота интервала, предшествующего медианному (12 + 50 = 62);

f_ме – частота медианного интервала ( 95).

Ме =60 + 20 * (99 – 62) / 95 = 67, 79 тыс. руб.

В среднем чистая прибыль составляет 67, 79 тыс. руб.

Построим графического изображения вариационных рядов, используя кумулятивной кривой.При помощикумуляты (кривой сумм)изображается ряднакопленных частот. Накопленные частоты определяется путем последовательного суммирования частот по группам, и показывают, сколько единиц совокупности имеют значения признака не больше, чем рассматриваемое значение.

При построении кумуляты интервального вариационного ряда по оси абсцисс откладываются варианты ряды, а по оси ординат накопленные частоты, которые наносят на поле графика в виде перпендикуляров к оси абсцисс в верхних границах интервалов. Затем эти перпендикуляры соединяют и получают ломаную линию, т. е. кумуляту.

Таблица 8

Данные для расчета кумуляты

Величина чистой прибыли, тыс. руб. х	Число фирм, f	Середина Интервала, Х´ = (хк +хн) / 2	Накопленная частота
А
20 – 40
40 – 60
60 – 80
80 – 100
100 – 120
ИТОГО		-	-

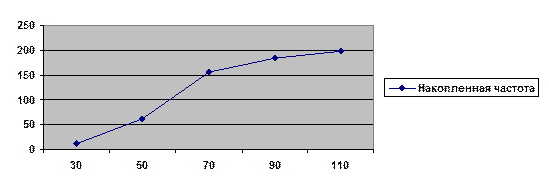
Рис. 2. Кумуляты распределение фирм по чистой прибыли

Построим гистограмму,при построении которой на оси абсцисс откладываются величины интервалов, а частоты изображаются прямоугольниками, построенными на соответствующих интервалах.

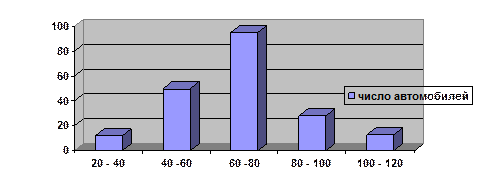
Рис. 3.Гистограмма распределения фирм по чистой прибыли

Расчет ошибки выборки

В целях изучения норм расхода сырья, которая влияет на оптимальный размер расходов, что тем самым может увеличит прибыль, важно рассмотреть анализ расхода сырья, а именно анализ числа изделий по весу. Проведена 1 процентная механическая выборка, в результате которой получено следующее распределение изделий по весу:

Таблица 9

Исходная таблица

Вес изделия, г.	Число изделий, шт.
До 2000
2000 – 2050
2050 – 2100
2100 – 2150
Свыше 2150
итого

Известно также, что к стандартной продукции относятся изделия с весом 2000 грамм до 2150 грамм.

1. Размах вариации (Р) определяется как разность между наибольшим (Х мак.) и наименьшим (Х мин.) значениями вариантов:

Р= Х мак. – Х мин.

Т. к. вариация незаконченная, то закончим и начнем на величину большее и меньшее длины интервала, соответственно, т. е. Х мин. равен 1950 (2000 –50), а Х мак. равен 2200 (2150 +50).

Р = 2200 – 1950 = 250.

Размах вариации составил 250.

2. Чтобы дать обобщающую характеристику распределения отклонений, исчисляют среднее линейное отклонение dср., которое учитывает различия всех единиц изучаемой совокупности и определяется по следующей формуле:

dср = ∑( х_i– х_ср.)*f / ∑ f,

где х_i – средняя вариация, которая определяется полусумма границ интервала;

f – признак распределения.

х_ср. – среднее значение признака распределения, равное максимальному значению второго признака (2075)

Расчеты будут вносится в рабочую таблицу 6.2.

Таблица 10

Расчетная таблица

Вес изделия, г.	Число изделий, шт.	Расчетные показатели
х1i =( хi+1 + хi)/2	х1i* f	(хi–хср.)= хi - 2075	(хi – хср.) *f	(хi – х хср.)2	(хi – хср.)2 * f
1950 - 2000				- 100	-400
2000 – 2050				- 50	-750
2050 – 2100
2100 – 2150
2150 - 2200
итого

dср= 2750/100 = 27,5 грамм

3. Показатель дисперсии (σ²) определяется как средняя из отклонений, возведенных в квадрат (х_i – х х_ср.)²

σ² = ∑ (х_i – х_ср.)² / n-1

σ² = 93500 / 4= 23375

4. Корень квадратный из дисперсии (σ²) представляет собой среднее квадратичное отклонение (σ)

σ = √ σ² =√23375 = 152,89 грамм.

Среднее квадратичное отклонение получилось не маленькое, что свидетельствует о ненадежности средней в весе изделия.

5. Коэффициент вариации (ν) определяется по формуле:

ν= σ/ х_ср*100% =152,89 /2075*100% = 7,37%

6. Определим значение средней ошибки выборки:

μ_w ~ √( w*(1- w)/n) *(1- n/N), где

w –показатель частности

Поскольку из 100 изделий, попавших в выборку n, 90 ед. оказались стандартными (15+55+20), соответствующие весу от 2000 до 2150 грамм, (m), то

w = m/ n=90/100=0,9

μ_w ~ √(0,9(1-0,9)/100)*(1-100/2000)= +0,029

Для показателей среднего веса изделия

μ_х=√ (σ²/ n)*(1- n/N)= 23375/100*0,95= +222,06 грамм

Полученные значения средней ошибки выборочной доли (+0,029) и средней ошибки выборочной средней (+222,06 грамм) необходимы для установления возможных значений генеральной доли (p) и генеральной средней (х_{ср 1}).

· Если ошибку выборки надо рассматривать с вероятностью 0,997, то тогда при значении t = 3,0 расчет характеристик генеральной совокупности следующий:

Доля стандартных изделий

p = w +_-t * μ_w=0,9+_-3*0,029

т. е. от 0.9-0,087=0,813 до 0.9+0,087=0,987

Значит, в 99 случаях из 100 удельный вес стандартных изделий во всей партии будет находится в пределах от 81,3% до 98,7%.

Средний вес изделия, грамм

х_{ср 1}= х_{ср -}⁺_{_} t * μ_х=2075_-⁺ 3*222,06

т. е. от 1408,82 до 2741,18

следовательно, с вероятностью, равной 0,997 можно утверждать, что средний вес изделия во всей партии находится в пределах от 1408,82 до 2741,18 грамм.

· Если ошибку выборки надо рассматривать с вероятностью 0,954, то тогда при значении t = 2,0 расчет характеристик генеральной совокупности следующий:

Доля стандартных изделий

p = w +_-t * μ_w=0,9+_-2*0,029

т. е. от 0.9-0,058=0,842 до 0.9+0,058=0,958

Значит, в 99 случаях из 100 удельный вес стандартных изделий во всей партии будет находится в пределах от 84,2% до 95,8%.

Средний вес изделия, грамм

х_{ср 1}= х_{ср -}⁺_{_} t * μ_х=2075_-⁺ 2*222,06

т. е. от 1630,88 до 2519,12

следовательно, с вероятностью, равной 0,954 можно утверждать, что средний вес изделия во всей партии находится в пределах от 1630,88 до 2519,12

Список литературы

1. Громыко Г.Л. Статистика. – М.: Изд-во МГУ им. Ломоносова, 2008.

2. Гусарев В.М. Теория статистики. – М.: ЮНИТИ, 2008.

3. Общая теория статистики: Статистическая методология в коммерческой деятельности: учебник для вузов / Под ред. А.С. Спирина и О.Е.Башиной. – М.: Финансы и статистика, 2008.

4. Социальная статистика: учебник для вузов / Под ред. И.И.Елисеевой. – М.: Финансы и статистика, 2007.

5. Статистика: Курс лекций для вузов / Под ред. В.Г.Ионина. – М.: ИНФРА-М, 2006.

6. Чернова Т.В. Экономическая статистика: Учебное пособие. Таганрог: Изд-во ТРТУ, 2006.

7. Экономическая статистика: Учебник / Под ред. Ю.Н.Иванова. – М.: ИНФРА-М, 2008.