Методы оценки и учета рисков в финансовых решениях
Традиционные методы оценки риска
Для определения величины финансового риска необходимо знать все возможные последствия отдельного действия (решения) и вероятность этих последствий.
Математическое ожидание какого-либо события = абсолютная величина этого события * на вероятность его наступления.
Эффективность какой-либо операции и риск взаимосвязаны. Методы оценки риска используются при принятии инвестиционных решений.
Пример:
2 варианта вложения капитала в одно мероприятие:
А - обеспечивает прибыль 15 т. р. с вероятностью 0,6
В - обеспечивает прибыль 20 т. р. с вероятностью 0,4
Ожидаемое получение по каждому из мероприятий:
15000*0,6=9000
20000*0,4=8000
Методы определения вероятности наступления события
1. объективный метод - вычисление частоты, с которой происходит данное событие;
2. субъективный метод - вычисление на основе субъективных критериев, которые базируются на различных предположениях (личный опыт, суждения оценивающего, оценка эксперта, мнение финансового консультанта и т.д.)
Критерии измерения степени риска:
1. среднее ожидаемое значение - значение величины события, связанное с неопределенностью ситуаций; является средневзвешенной для всех возможных результатов;
2. изменчивость (колеблемость) возможного результата - степень отклонения ожидаемого значения от средней величины.
Если известны все результаты и известны вероятности получения этих результатов, то это вероятностное распределение.
Вероятностное распределение – это предоставление результата в ситуации, когда известны все возможные значения результата и вероятности получения этих значений.
Пример:
Актив А приобретен за 350 ден. ед. Существуют три варианта продажи данного актива, через год после приобретения: за 420 ден. ед. c 25 %, за 400 ден. ед. с 50 %, за 380 ден. ед. с 25 %.
Доход определяется: (цена продажи – инвестиции)/инвестиции
Доход - 70, 50 и 30 ден. ед.
Вероятностное распределение:
цена продажи 420 400 380
вероятность 25% 50% 25%
доход 70 50 30
доходность 20% 14,3% 8,6%
Ожидаемая доходность = 20*0,25+14,3*0,5+8,6*0,25=14,3%
Ось у - доходность, ось х - вероятность.
Чем выше y, тем больше вероятность, что ожидаемая вероятность ближе к фактической (тем ниже риск принимаемого решения).
Нормальное распределение вероятностей предполагает, что среднее состояние доходности соответствует самой большой вероятности, а далее значение вероятностей равномерно уменьшается при удалении от нормы как в одну, так и в другую сторону, стремясь к нулю в крайних положениях.
Нормальное распределение достаточно полно отражает ситуацию и дает возможность использования ограниченной информации, получать возможность рисков инвестиционных проектов.
Концепция риска и дохода и методы оценки риска
Финансовый риск – вероятность возникновения убытков или недополучения доходов по сравнению с прогнозируемым вариантом
Риск финансового актива – степень вариабельности дохода (доходности), который может быть получен в результате операций с этим активом
Рискованность актива тесно связана с его доходностью, а актив, с которым связан размер возможно больших потерь, рассматривают как более рисковый актив. К более рисковым активам применяют более высокие требования доходности.
Доходность актива (норма прибыли) – доход, исчисленный в процентах к первоначальной стоимости актива.
Вывод: финансовый менеджер при принятии финансового решения исходит из того, что требуемая (ожидаемая) доходность и риск актива изменяются в одном направлении (пропорционально друг другу)
Традиционные методы оценки риска
1) размах вариации
2) дисперсия
3) среднее квадратическое (стандартное) отклонение
4) коэффициент вариации
Размах вариации
Пусть рассматривается детерминированный ряд статистических величин (абсолютных или относительных)
х1, х2, х3, …, хn – доход (доходность) – признак ряда
R = x max – x min
R – размах вариации, x max – максимальное значение признака ряда, x min - минимальное
Чем выше значение R, тем выше степень риска по данному проекту.
Ограничения (недостатки) метода:
· грубая оценка степени вариации значений признака;
· величина R существенно зависит от крайних значений ряда
· применение метода в сравнительном анализе ограничено из-за его абсолютности;
Дисперсия
- средний квадрат отклонений значений признака от его средней величины. Фигурируют вероятностные характеристики.
σ2 = 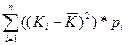
pi – вероятность, соответствующая данному значению доходности
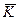 = ∑Kipi, среднее ожидаемое значение доходности
= ∑Kipi, среднее ожидаемое значение доходности
n – число возможных отклонений от ожидаемого значения
ki – значение доходности по данному активу
