Занятие 8. Налоги и начисление процентов

Налогообложение играет большую роль в экономике любой страны. Во многих странах налогом облагают проценты, полученные при помещении некоторой суммы на депозит, что уменьшает реальную наращенную сумму и реальную доходность финансовой операции.

Налоги, начисляемые на полученные проценты, уменьшают реальную доходность финансовой операции. Учет налога при определении наращенной суммы приводит к уменьшению ставки.

Введем обозначения:

t- ставка налога на проценты

T – общая сумма налога

F- наращенная сумма до выплаты налога на проценты

F_t - наращенная сумма после выплаты налога на проценты

P – вложенная сумма

n – продолжительность финансовой операции

Пусть r - простые ссудные проценты, тогда величина процентов, начисленных за период n, равна Pnr.

Сумма налога на начисленные проценты равна Т=Pnrt (8.1)

Наращенная сумма после выплаты налога на проценты равна

F_t = P[(1+r(1-t)n] (8.2)

Таким образом, налог на проценты уменьшает процентную ставку и вместо ставки r применяется ставка (1-t)r.

Пусть на сумму Р за период времени n начислялись простые учетные проценты по учетной ставке d. Величина начисленных процентов равна Pnd/(1-nd).

Сумма налога на начисленные проценты составит

T=Pndt/(1-nd) (8.3)

Наращенная сумма после выплаты налога на проценты равна

F_t = F-T=P(1-ndt)/(1-nd) (8.4)

Пусть r - сложные ссудные проценты, тогда величина процентов, начисленных за период n, равна P[(1+r)ⁿ -1]

Сумма налога на начисленные проценты равна

Т=P[(1+r)ⁿ -1]t (8.5)

Наращенная сумма после выплаты налога на проценты равна

F_t =P[(1+r)ⁿ (1-t)+t] (8.6)

В случае сложных процентов налог на начисленные проценты можно выплачивать как в конце финансовой операции, так и каждый год. При этом общая сумма исчисленного налога не изменяется.

Пусть на сумму Р за период времени n начислялись сложные учетные проценты по учетной ставке d. Величина начисленных процентов равна

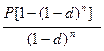
Сумма налога на начисленные проценты равна 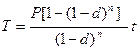(8.7)

Наращенная сумма после выплаты налога на проценты равна

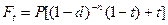(8.8)

Пусть на сумму Р за период времени n начислялись непрерывные проценты по ставке δ.

Сумма налога на начисленные проценты равна T=P(e^δ -1)t (8.9)

F_t =P[e^δ (1-t)+t] (8.10)

Цель проведения занятия -научиться рассчитывать влияние налогов на доходность финансовых операции, используя формулы финансовых вычислений.

Типовые задачи с решениями

Задача 1.На депозит поместили 300 тыс. руб. на полтора года. Банк начисляет простые учетные проценты по ставке под 14% годовых. Определить наращенную сумму с учетом уплаты налога на проценты, если ставка налога на проценты составляет 12% годовых.

Решение

Используем формулу (8.4)при P=300; n=1,5; t=0,12; d=0,14

F_t =300(1-1,5∙0,14∙0,12)/ (1-1,5∙0,14)= 370,018

Наращенная сумма с учетом налога на проценты составит 370018 руб.

Задача 2.На депозит поместили 300 тыс. руб. на полтора года. Банк начисляет простые проценты по ставке под 16% годовых. Определить наращенную сумму с учетом уплаты налога на проценты, если ставка налога на проценты составляет 12% годовых.

Решение

Используем формулу (8.2) при P=300; n=1,5; t=0,12; r=0,16

F_t =300[1+∙0,16 (1-∙0,12)1,5]= 360,336

Наращенная сумма с учетом налога на проценты составит 360336 руб.

Задача 3.На вклад в 2 млн. руб. в течение 4 лет каждые полгода начислялись сложные проценты по годовой номинальной ставке 12% годовых. Определить наращенную сумму после уплаты налога на проценты, если ставка налога на проценты составляет 8% годовых.

Решение
Запишемформулу (8.6) с учетом полугодового начисления процентов:

F_t =P[(1+r/m)^nm (1-t)+t]

при P=2; r=0,12; n=4; m=2; t=0,08

F_t = 3,09268

Наращенная сумма с учетом налога на проценты составит 3 092 680руб.

Задача 4.Для участия в некотором проекте предпринимателю необходимо 280 тыс. руб. Между тем он располагает суммой 250 тыс. руб. С целью накопления необходимой суммы предприниматель собирается положить 250 тыс. руб. в банк. Предлагаемая банком ставка по вкладам равна 14% годовых. Какое количество дней необходимо для накопления требуемой суммы с учетом уплаты налога на проценты, если банк начисляет простые проценты, использует точный процент с точным числом дней, а ставка налога на проценты равна 1%?

Решение

Обозначим через Х необходимое число дней, тогда формула (8.2) запишется в виде:

F_t = P[(1+r(1-t)Х/ 365]

При F_t =280; Р=250; r=0,14; t=0,01

280=250∙[1+0,014∙(1-0,01)X / 365]

Решая полученное уравнение относительно Х, получаем:

Х=316,017

Для накопления требуемой суммы необходимо 317 дней.

Задача 5.Клиент положил в банк 60 тыс. рублей под простую процентную ставку 10% годовых и через полгода с учетом налога на проценты получил 62,8 тыс. руб. Определить ставку налога на проценты.

Решение

Из формулы (8.2) выразим ставку налога на проценты

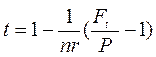
При F_t =62,8; Р=60; r=0,1; n=0,5

t=0,067

Ставка налога на проценты равна 6,7%.