Систематический и несистематический риск отдельного актива

Лауреат Нобелевской премии У. Шарп в 1964 г. выделил две составляющие общего риска любого актива (этот риск количественно может быть измерен дисперсией отклонения от ожидаемого значения):

1) специфический риск корпорации (риск эмитента), т.е. диверсифицируемый риск, который устраняется комбинацией ценных бумаг в портфеле;

2) недиверсифицируемый (систематический или рыночный) риск. Общий риск актива (например, ценной бумаги) σ2 общий риск = σ2специф. + σ2 систем.

Диверсифицируемый риск связан с финансовым положением эмитента рассматриваемой ценной бумаги с присущим ему коммерческим и финансовым риском.

Рыночный риск возникает по независящим от эмитента причинам, т.е. не является свойственным только данной корпорации — эмитенту ценной бумаги. Компонентами систематического (рыночного) риска являются риск покупательной способности, процентный риск. Так как, формируя портфель, инвестор может исключить диверсифицируемый риск (подбирая активы, коэффициент корреляции которых не равен +1), то риск хорошо диверсифицированного портфеля будет зависеть от рыночного риска включенных в этот портфель ценных бумаг.

Комбинируя активы в портфель, инвестор тем самым сокращает риск, т.е. уменьшает значение дисперсии по портфелю. С увеличением числа активов в портфеле риск портфеля снижается очень быстро при небольшом общем числе активов, и снижение риска замедляется при многочисленных комбинациях, так как все больше активов положительно коррелируют друг с другом

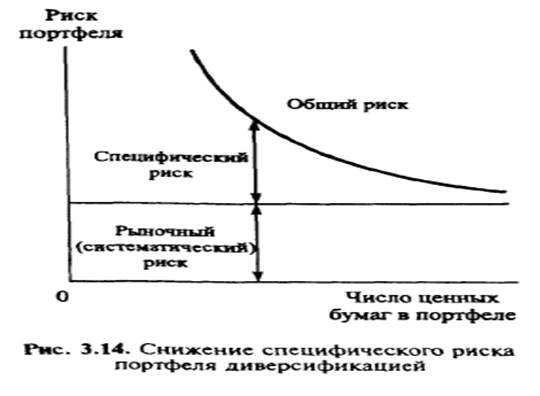
Значительное сокращение специфического риска может быть достигнуто формированием небольшого портфеля (порядка 30 различных ценных бумаг).

Абсолютное нивелирование специфического риска требует включения в портфель всех активов, обращающихся на рынке, т.е. формирования рыночного портфеля.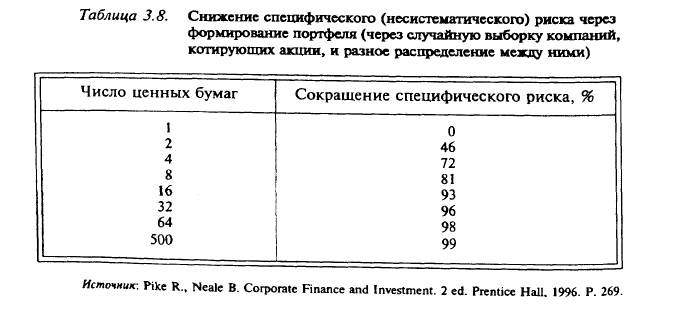

У. Шарп ввел концепцию β (бета) для измерения систематического (рыночного) риска актива. Чтобы оценить, как включение новой ценной бумаги в хорошо диверсифицированный портфель повлияет на его риск, не столь важно знать общий риск этой ценной бумаги σ2 общий. Достаточно знать рыночный риск σт2 и определить, насколько чувствительна данная ценная бумага по отношению к движению рынка (σ2 Р=σ2 м). Эта чувствительность измеряется β - коэффициентом. β показывает уровень изменчивости актива (например, ценной бумаги) по отношению к рыночному портфелю (усредненному активу). Статистически β акции j можно определить как

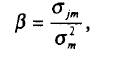
где σjm — ковариация между доходностью акции j и рыночной доходностью, определяемой по динамике рыночного индекса (индекса фондового рынка, на котором котируется данная акция);

σт2 — дисперсия рыночной доходности.

Таким образом, β-коэффициент есть наклон линии, отражающей зависимость доходности акции от доходности рынка. Эта линия называется характеристической линией (прямой).

Например, АО "Сургутнефтегаз" имело β = 1,52 на октябрь 1996 г. Если бы в 1997 г. не произошло изменений в финансовой политике предприятия (так как β зависит от структуры капитала предприятия, принимаемых инвестиционных проектов), то при возрастании рынка (или портфеля из всех рыночных акций) в среднем на 1 % рыночная цена акции АО возросла бы на 1,52% и, следовательно, доходность инвестирования в акцию возросла бы за год на 1,52%.

Если бы рынок упал на 10%, то цена акции "Сургутнефтегаз" снизилась бы на 15,2%.

Акции с β меньше единицы и больше нуля движутся в том же направлении, что и рынок, но более медленно. Рынок можно рассматривать как портфель из всех акций, и, следовательно, средняя акция на рынке (среднего риска) имеет Д = 1. Коэффициент β позволяет предсказать, как изменится цена актива (возрастет или снизится) при знании поведения рынка. Прогноз поведения цены актива (через β) позволяет оценить риск инвестирования и ожидаемую доходность. β портфеля есть средневзвешенный коэффициент Д ценных бумаг, включенных в портфель. Чем больше риск портфеля, тем больше должна быть компенсация в виде повышения доходности. При эффективно составленном портфеле диверсифицируемый риск активов, включаемых в него, можно не учитывать, на этот риск не предусматривается компенсация в виде повышения доходности. Только рыночный риск (или бета-риск, систематический риск) должен быть компенсирован.

?Может ли актив иметь отрицательное значение β ? Что это означает с точки зрения рыночного риска? Какую доходность можно ожидать от этого актива на долгосрочном отрезке времени?

Если допустить возможность безрискового займа и ссужения денег, то имеют ли построенные эффективные портфели специфическую составляющую риска?

Запомните синонимы, используемые для обозначения двух видов риска: систематический риск — недиверсифицируемый риск, рыночный риск, бета-риск;

несистематический риск — специфический риск, диверсифицируемый риск, уникальный риск.

?Верно ли утверждение: "Если акция имеет коэффициент р, равный нулю, то она не является безрисковой для инвестора, который владеет ею не в портфеле; только портфельное владение позволяет нивелировать риск для акции с β = 0"?

РЫНОЧНЫЙ РИСК АКЦИИ И ХАРАКТЕРИСТИЧЕСКАЯ ПРЯМАЯ

Движение цены акции определяется систематическим и несистематическим риском. Систематический риск, обусловленный макрофакторами, присущ всем акциям рынка. Можно рассматривать связь мультипликатора меры риска со степенью чувствительности отдельной акции к изменению рыночного портфеля. Чем выше чувствительность, тем выше должен быть мультипликатор.

Характеристическая прямая отражает связь ожидаемой доходности акции kj и ожидаемой доходности рынка kт. Степень зависимости графически представляется наклоном характеристической прямой (рис. 3.15), численное значение равно тангенсу угла, образуемого прямой с горизонтальной осью.

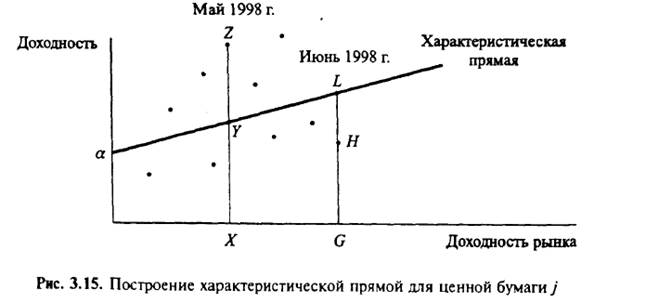
Рисунок показывает множество наблюдений за один месяц 1998 г. В отличие от ожидаемых значений (лежащих на характеристической прямой) на рис. 3.15 большинство значений отклоняются из-за влияния случайных, несистематических факторов. Например, точка 2 (общая доходность ценной бумаги на май 1998 г.) отражает превышение над доходностью, связанной с движением рынка XY, на величину нерыночной составляющей доходности YZ. Обратная ситуация наблюдалась в июне 1998 г. (точка H), когда фактическая доходность была ниже "предписываемой" по характеристической прямой.

Фактические значения доходности объясняются следующим образом.

Изменения kj с течением времени в соответствии с характеристической прямой отражают влияние рыночных факторов. Эти факторы оказывают систематическое воздействие на ценную бумагу j. Отклонения от характеристической прямой отражают влияние специфических для корпорации у факторов.

Следует отметить, что понятие изменения доходности для акции отражает изменение и рыночной цены, и дивидендов. При рассмотрении рыночного портфеля дивидендная составляющая доходности может быть измерена как средняя дивидендная доходность рыночного индекса.

На практике отсутствует возможность оценки ожидаемых значений доходности как по конкретной бумаге, так и по рыночному портфелю.

Теоретическая посылка оценки коэффициента 0 по ожиданию будущих изменений заменяется оценкой по прошлым наблюдениям поведения доходности kj и kт. Насколько прошлые изменения могут быть гарантией будущего развития (часто ожидания инвесторов основываются на вероятностном распределении прошлых результатов), настолько Д может стать индикатором изменения Л в зависимости от изменения kт. По прошлым данным строится однофакторная модель вида

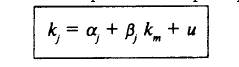
где фактором является зависимость доходности ценной бумаги у от рыночного индекса (доходность рыночного индекса kт), .j и .j; являются истинными оценками и ., и — случайная переменная. Эта регрессионная модель носит название рыночной модели (market model, singel-index model).

Модель рассматривает зависимость премии за риск по ценной бумаге j от премии за риск по рыночному индексу, j — доходность ценной бумаги) при нулевой доходности рынка, т.е. когда влияние рыночного риска отсутствует.

Соответственно а (альфа) показывает, какую доходность ценная бумага обеспечит владельцу за диверсифицируемый (специфический) риск. В некотором смысле это дополнительная премия по сравнению с безрисковым активом для случая нулевой премии за рыночный риск. При нулевой премии за рыночный риск каждая ценная бумага в состоянии рыночного равновесия будет иметь нулевые значения коэффициентов. Средневзвешенная коэффициентов всех ценных бумаг равна нулю, при этом по некоторым бумагам значение может быть положительным, а по некоторым — отрицательным. Графически «-коэффициент равен отрезку, отсекаемому на оси ординат.

Прямая, отражающая зависимость доходности акции j от фондового индекса, строится на основе регрессионного анализа (минимизируется сумма квадратов отклонений значений наблюдаемых точек на графике и соответствующих точек, лежащих на прямой). Обобщенным показателем степени связи доходности акции и индекса является коэффициент детерминации или коэффициент R2. R2 =(Коэффициент корреляции)2. Например, численное значение R2 = 0,8 показывает, что 80% вариации доходности акции может быть объяснено изменениями доходности индекса.

При большом количестве наблюдений и близости точек к характеристической прямой R 1.

Пример построения характеристических прямых для двух российских эмитентов показан на рис. 3.16. В качестве индекса выбран индекс РТС, интервал наблюдений 15 календарных дней (10 торговых сессий), период 1996 г. - май 1998 г. По РАО "ЕЭС России" . = 1,15; R2 = 0,8. По "Норильскому никелю" . = 0,97; R = 0,66.

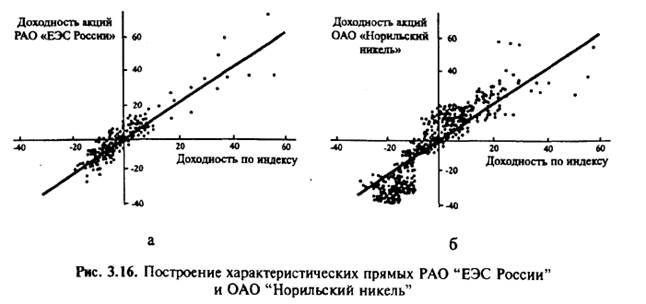
В ряде случаев представляет интерес анализ отраслевой чувствительности, т.е. построение зависимости доходности отраслевого индекса от индекса фондового рынка. Например, рассчитаны коэффициенты энергетического, нефтяного индексов и индекса предприятий электросвязи по индексу РТС с интервалом 15 дней за период январь — май 1998 г[3]:

Стабильность β-коэффициента для портфеля (в данном случае отрасль рассматривается как портфель) значительно выше, чем для отдельной компании, и связь с рынком также выше, что характеризуется высокими значениями коэффициента детерминации для портфеля.

Если предположить, что российский инвестор имеет возможность вкладывать средства в рисковые активы по всему миру, то следует оценивать .- коэффициент, определяющий волатильность (чувствительность, изменчивость) по отношению к мировым индексам.