Блок 12. Анализ экономической эффективности

В этом блоке рассматривается соотношение всевозможных результатов и всевозможных затрат.

результаты: доходы, прибыль, дивиденды;

затраты: основные фонды, заработная плата, материальные ресурсы.

Детерминированные методы и модели анализа.

Общие положения детерминированного анализа.

Экономический анализ строится на изучении зависимости между затратами (факторами) и результатом. Все эти зависимости описываются с помощью факторных моделей. Выделяются детерминированные факторные модели и статистические факторные модели.

К детерминированным факторным моделям можно отнести:

- аддитивные модели 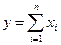(сумма);

- мультипликативные модели (45%) 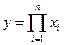(произведение)

пример – объём выпуска продукции X = P*L;

- кратные модели (45%) ;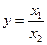

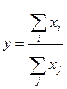
пример ; ;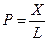

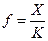Для анализа факторных моделей наибольшее распространение получили интегральный и индексный методы.

Интегральный метод представляет собой связь между результатом и фактором в виде функциональной зависимости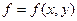

Полный дифференциал такой функции:

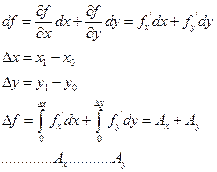
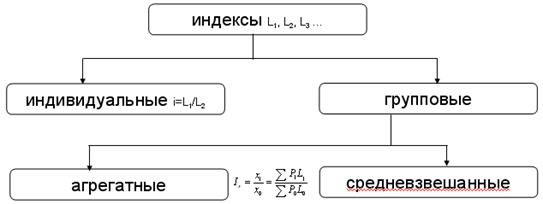
Индексный метод характеризует изменение относительных показателей экономического процесса. Индексы бывают индивидуальные и групповые.

Интегральный метод.

Мультипликативная модель.

Предположим, что модель имеет вид ,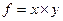

тогда 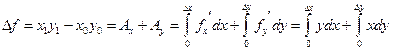, принимая во внимание, что

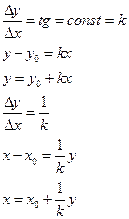
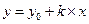
y – будущее значение

x – величина изменяемого фактора

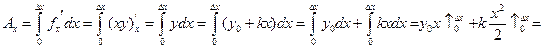
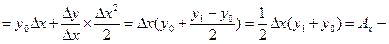влияние фактора х на результат z.

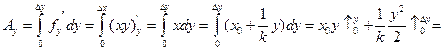
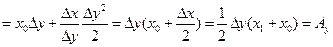
Пример: результат 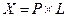P – производительность, L – численность.

Кратная модель.

Предположим, что модель имеет вид 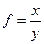, тогда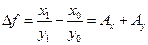

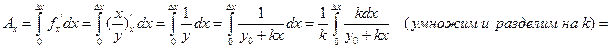
табличный интеграл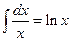

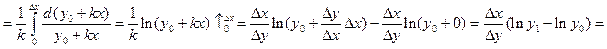
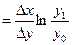
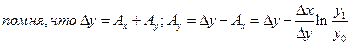
Пример: 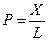(производительность труда).

Индексный метод.

Индекс – это показатель измерения роста экономического процесса (темп роста). Это относительный показатель. Также позволяет разложить сложный экономический процесс на факторы и исследовать влияние каждого фактора на результат (только для двухфакторной модели).

пример: 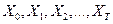- динамика роста валового продукта;

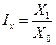- индекс роста валового продукта;

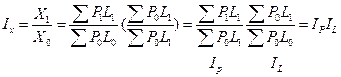
домножили на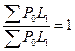

Аналогичный приём используется при расчёте абсолютного влияния факторов на результат (абсолютное влияние)

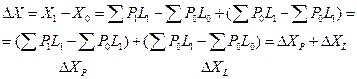
Недостатком индексного метода является то, что он справедлив только для двухфакторных моделей). Между тем существует метод цепных подстановок, который позволяет определять абсолютное влияние факторов в многофакторной модели.

предположим, что

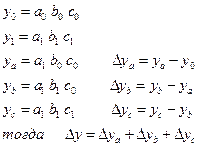
Статистический метод. Общие положения статистического анализа.

Статистический анализ выступает в качестве инструмента, который позволяет расширить систему методов экономического анализа. Специфика системного анализа заключается в том, что и факторы и результат рассматриваются как случайные значения. Для задания случайных величин необходимо определить правило, по которому каждому возможному значению факторов сопоставляется вероятность его появления. Это правило принято называть законом распределения вероятности. Для описания этого закона достаточно задать функцию распределения вероятности.

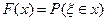
Наряду с функцией распределения вероятности получило широкое распространение функция плотности распределения вероятности:

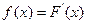
Её свойства:

1)

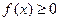
2)

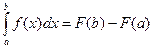
3)

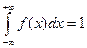
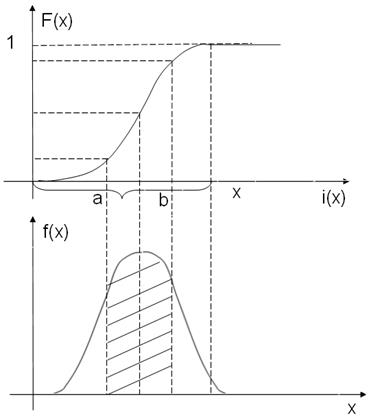
В обычной экономике мы имеем дело с конкретными случайными выборками. Поэтому стоит задача по этим выборками определить функцию распределения вероятности и функцию плотности распределения вероятности. Вводится эмпирическая (выборочная) функция распределения вероятности. Определяется следующим образом:

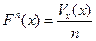, где

V_x – количество случайных значений в выборке, которое меньше x.

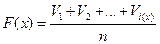, где

i(x) – последний номер

Полученная эмпирическая функция распределения называется комуметой.

Эмпирическая функция плотности распределения вероятностей определяется таким образом:

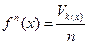, где

V_k(x) – количество случайных значений попавшее в интервал k, которое включает значение x.

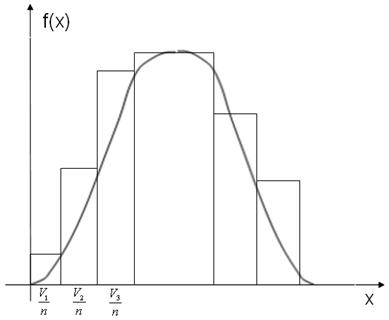
Представленная диаграмма является гистограммой, которая определяет эмпирическую функцию плотности распределения вероятности.

Полученные диаграммы позволяют дать характеристики вероятностного распределения. К этим характеристикам относятся: математическое ожидание, дисперсия, моменты и другие.

Математическое ожидание.

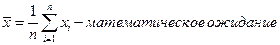
если поставить свою вероятность P, то

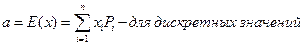
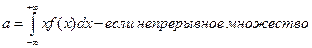
Дисперсия – разброс относительно среднего.

Дисперсия измеряется следующим образом:

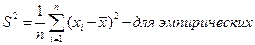
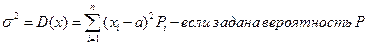
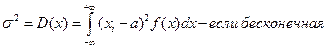
Полученные характеристики могут быть использованы для описания функций плотности распределения вероятности и в самой функции распределения вероятности. В частности для нормальных закономерностей:

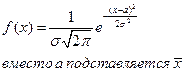
Корреляционный анализ.

Корреляционный анализ служит для измерения связи между случайными величинами.

пример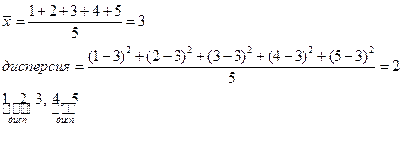

Наиболее простой характеристикой степени зависимости двух случайных величин является корреляционный момент. Корреляционный момент - среднее от произведения двух случайных величин. Корреляционный момент характеризуется тем, что для независимых случайных величин он равен 0.

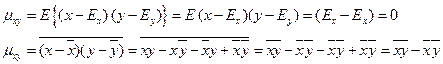
Недостатком корреляционного момента является то, что его величина зависит от размерности случайных величин. Для того, чтобы избежать этого недостатка используется операция нормирования. Тогда корреляционный момент представляется в виде коэффициента корреляции.

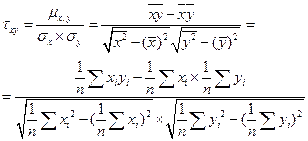
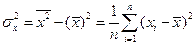
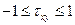
если 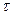=+1 – детерминированная связь;

если 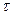=+0,5 – статистическая связь;

если 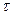<0 – обратная связь

Регрессионный анализ.

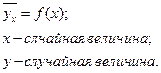
Важнейшей задачей статистического анализа является определение зависимости средней величины результата от изменения факторов. Эта зависимость называется корреляционной, а уравнения связи называются уравнением регрессии. Простейший вид уравнения регрессии:

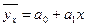
Для получения данного уравнения необходимо определить коэффициенты a₀ и a₁, которые называются коэффициенты регрессии. Для определения оптимальных коэффициентов регрессии можно воспользоваться методом наименьших квадратов.

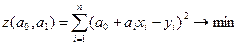
Суть метода наименьших квадратов – найти такие а₀ и а₁, чтобы между задуманным и фактическим значениями y_i было минимальное расхождение.

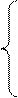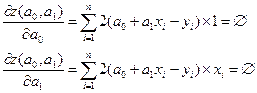
если просуммируем:

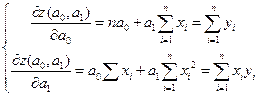
Из решения системы уравнений представленных выше определяется а₀ и а₁. Оно будет наилучшим образом описывать случайны процесс.

Если уравнение регрессии зависит от нескольких факторов и эта зависимость линейная, то такое уравнение называется линейным множественным уравнение регрессии.

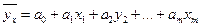
Для построения множественного линейного уравнения регрессии надо определить коэффициенты а₀, a_n.

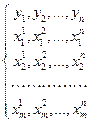
Для определения a₀, a₁, …, a_m (коэффициентов регрессии) используется метод наименьших квадратов.

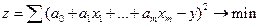
Если продифференцировать по каждому коэффициенту регрессии и приравнять к нулю (0), то получим следующую систему уравнений:

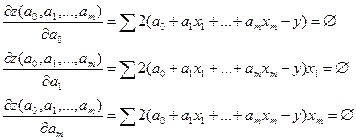
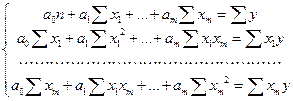
m+1 неизвестных, m+1 уравнений

Из решений системы определяем а₀, а₁, …, а_m.

Наряду с линейными уравнениями регрессии широкое распространение имеют множественные нелинейные уравнения регрессии:

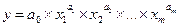
Для того, чтобы определить коэффициенты регрессии необходимо данную функцию прологарифмировать:

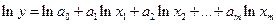
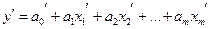
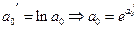
Взяли и записали дифференцирование вместо логарифма и получили линейное множественное уравнение регрессии.

Уравнения регрессии необходимы для описания связи между результатами и факторами влияния, то есть определяют влияние факторов на результат.