Дисконтирование по простым процентным ставкам

При заключении финансовых соглашений часто приходится решать задачу, обратную задаче нахождения наращенной сумме. Например, по заданной сумме F, которую предполагают получить (или уплатить) через время t, требуется определить величину капитала P, который необходимо инвестировать в данный момент, чтобы через время t при постоянной процентной ставке получить сумму F. Аналогичная задача (нахождение P и F) возникает и в том случае, когда проценты удерживаются непосредственно при выдаче ссуды (P).

Такое движение денежных средств от будущего к настоящему носит название дисконтирования. Говорят, что капитал F дисконтируется; величина удержанных процентов часто называется дисконтом. Капитал P, найденный с помощью процесса дисконтирования суммы F, называется приведённой(современной, текущей, капитализированной) стоимостью. При дисконтировании решается задача нахождения такой величины капитала P, которая через n лет при наращении по простым процентам по ставке r будет равна F:

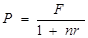(3.4)

Дисконт-фактор (дисконтный множитель) 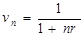показывает долю капитала P в F. Дисконтный множитель также называется коэффициентом дисконтирования и представляет собой величину, обратную множителю наращения простых процентов. В качестве ставки дисконтирования используется процентная ставка r. Разность D_r между F и P называется дисконтом:

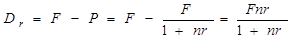(3.5)

Пример

Из какого капитала можно получить 3,4 млн. руб. через три года наращением по простым процентам при ставке 12%?

Пользуясь формулой (3.4.1), где F=3,4; n=3; r=0,12; получим

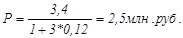
Очевидно, что D_r=F-P=3,4-2,5=0,9 млн. руб.

Банковское дисконтирование, или банковский учёт применяется при операции по так называемому учёту векселей банком или другим финансовым учреждением.

Рассмотрим наиболее распространённую ситуацию, когда владелец векселя на сумму F (сумма к погашению) предлагает банку раньше срока оплаты векселя купить его. Такая покупка векселя у владельца до наступления срока оплаты по цене, меньше той суммы, которая должна быть выплачена по векселю в конце срока, называется дисконтированием векселя. Сама операция дисконтирования векселя часто называется учётом векселя. Сумму, которую получает векселедержатель при досрочном учёте векселя, называется дисконтированной величиной векселя.

Таким образом, векселедержателю досрочно выплачивается обозначенная в векселе сумма за вычетом определённых процентов, удерживаемых банком в свою пользу и нередко называемых дисконтом. Дисконт (обозначаемый D_d) в этом случае представляет собой проценты, начисленные за время (n) от дня дисконтирования до дня погашения векселя на сумму (F), подлежащую уплате в конце срока. Если объявленная банком ставка дисконтирования равна d (учётная ставка), то

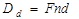(3.6)

и владелец векселя получит

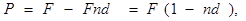(3.7)

где множитель (1-nd) называется дисконтным множителем или коэффициентом дисконтирования.

Очевидно, что чем выше значение дисконтной ставки, тем большую сумму удерживает банк в свою пользу. Учёт векселя чаще всего осуществляется способом 365/360.

Пример

Векселедержатель предъявил для учёта вексель на сумму 50 тыс. руб. со сроком погашения 28.09. вексель предъявлен 13.09.этого же года. Банк согласился учесть вексель по учётной ставке 30% годовых. Определить сумму, которую векселедержатель получит от банка.

Величина этой суммы рассчитывается по формуле (3.4.4) и при F=50 тыс. руб., n= 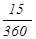года, d=0,3 составит:

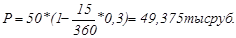
Разность между F и P, равная D_d, представляет собой комиссионные, удерживаемые банком в свою пользу за предоставленную услугу; в данном примере D_d=625 руб.

Задачи к семинару «Наращение и дисконтирование по простым процентным ставкам»

Задача 1. Найти величину дохода кредитора, если за предоставление в долг на полгода некоторой суммы денег он получил от заёмщика в совокупности 6,3 тыс. руб. При этом применялась простая процентная ставка в 10% годовых.

Задача 2. Сберегательный счёт был открыт 15 февраля, и на него была положена сумма в 5 тыс. руб. В следующем квартале 10 апреля на счёт поступили 3 тыс. руб. Затем 20 мая со счёта были сняты 2 тыс. руб., 1 сентября добавлена сумма в 1 тыс. руб. и 4 декабря счёт был закрыт. Все операции осуществлялись в течение года (невисокосного). Определить сумму, полученную владельцем счёта, если процентная ставка равнялась 12% годовых и применялся способ 365/360.

Задача 4. 100 млн. руб. положены 1-го марта на месячный депозит под 20% годовых. Какова наращенная сумма, ели операция повторяется 3 раза? (способы 365/365, 360/360).

Задача 5. Через полгода после заключения финансового соглашения о получении кредита должник обязан заплатить 2,14 тыс. руб. Какова первоначальная величина кредита, если он выдан под 14% годовых и начисляются обыкновенные проценты с приближённым числом дней?

Задача 6. Банк 12.04.09 учёл два векселя со сроками погашения соответственно 20.05.09 и 11.06.09. При этом в результате применения учётной ставки 18% годовых банком были удержаны комиссионные в размере 885 руб. Найти номинальную стоимость второго векселя, если первый вексель предъявлен на сумму 15 тыс. руб. используется способ 365/360.

Задача 7. В контракте предусматривается погашение обязательства в сумме 110 тыс. руб. через 120 дней. первоначальная сумма долга 90 тыс. руб. (365/360). Необходимо определить доходность ссудной операции для кредитора в виде ставки процента.