Средние показатели динамики
Методические советы по выполнению контрольной работы
Средние величины
Средними в статистике называются обобщающие показатели, выражающие типичные, характерные для определенных условий места и времени размеры и количественные соотношения явлений общественной жизни.
Средние величины можно рассчитать различными способами. Соответственно различают разные виды средних: агрегатные, арифметические, гармонические, геометрические и др.
При выборе вида средней для характеристики среднего уровня следует исходить из существа изучаемых явлений и наличия исходных данных. Если заданы варианты x и их частоты f, то для расчета их
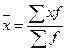
среднего значения пользуются средней арифметической взвешенной.
Если частоты f всех вариантов x равны, то пользуются средней арифметической простой.
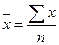 .
.
Если известны варианты в их суммарной значении по группам - W, но неизвестны частота повторения признака f, которая является сомножителем в W=xf, используются средней гармонической
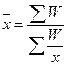 .
.
Выбирая вид средней, всегда надо имеет в виду, что средняя правильна тогда, когда имеет реальных экономический смысл.
Ряды динамики
Одной из важнейших задач статистики является изучение изменений анализируемых показателей во времени, т. е. их динамика. Эта задача решается при помощи анализа рядов динамики (или временных рядов).
Ряд динамики (или динамический ряд) представляет собой ряд расположенных в хронологической последовательности числовых значений статистического показателя, характеризующих изменение общественных явлений во времени.
В каждом ряду динамики имеются два основных элемента:
время t и конкретное значение показателя (уровня ряда) y.
Уровень может быть выражен абсолютными, средними и относительными величинами, надо уяснить, что особенности развития изучаемых явлений приводят к образованию различных по характеру динамических рядов: моментных и интервальных.
Статистический анализ рядов динамики, расчет аналитических показателей позволяют охарактеризовать интенсивность развития явления от периода к периоду (от даты к дате), а также среднюю интенсивность развития за исследуемый период, выявить основную тенденцию в развитии явления, осуществить прогноз развития на будущее, а также изучить сезонные колебания.
Краткие указания
Для изучения интенсивности изменения уровней ряда во времени исчисляются следующие показатели динамики: абсолютные приросты, коэффициенты роста, темпы роста, темпы прироста, абсолютные значения одного процента прироста.
Перечисленные показатели динамики можно исчислять с переменной или постоянной базой. Если производится сравнение каждого уровня с предыдущим уровнем, то получаются показатели динамики с переменной базой (цепные показатели динамики). Если каждый уровень сравнивается с начальным уровнем или каким-то другим, принятым на базу сравнения, то получаются показатели динамики с постоянной базой (базисные показатели динамики). База сравнения должна выбираться обоснованно, в зависимости от экономических особенностей явления и задач исследования.
Методы расчета показателей динамики представлены в табл. 1; они одинаковы для моментных и для интервальных рядов.
При расчете показателей приняты следующие условные обозначения:
yi – уровень любого периода (кроме первого), называемый уровнем текущего периода;
yi-1 – уровень периода, предшествующего текущему;
yk – уровень, принятый за постоянную базу сравнения (часто начальный уровень).
Т а б л и ц а 1
Показатели динамики
| Наименование показателя | Метод расчета | |
| с переменной базой (цепные) | с постоянной базой (базисные) | |
1. Абсолютный прирост ( 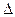 ) ) | 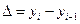 | 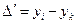 |
2. Коэффициент роста ( 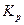 ) ) | 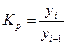 | 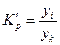 |
3. Темп роста ( 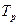 ),% ),% | 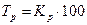 | 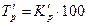 |
4. Темп прироста ( 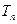 ),% ),% | 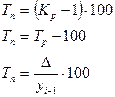 | 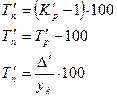 |
| 5. Абсолютное значение 1% прироста (А) | 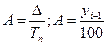 | 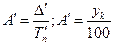 |
Для интенсивности развития за длительный период рассчитываются средние показатели динамики; метод их расчета представлен в табл. 2.
При написании формул приняты следующие условные обозначения: y1, y2…, yn – все уровни последовательных периодов (дат);
n – число уровней ряда;
t – продолжительность периода, в течение которого уровень не изменялся.
Т а б л и ц а 2
Средние показатели динамики
| Наименование показателя | Метод расчета |
1. Средний уровень ряда ( 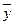 ): а) для интервального ряда c равными интервалами ): а) для интервального ряда c равными интервалами | 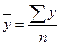 |
| б) для моментного ряда с равными интервалами | 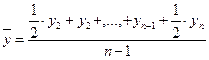 |
| в) для интервального ряда с неравными интервалами |  |
| г) для моментного ряда с неравными интервалами | 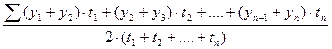 |
2. Средний абсолютный прирост ( 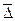 ) ) | 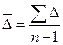 или или 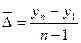 |
3. Средний коэффициент роста( 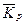 ) ) | 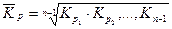 или или 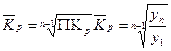 |
4. Средний темп роста ( 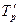 ),% ),% | 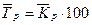 |
5. Средний темп прироста ( 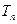 ),% ),% | 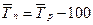 или или 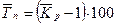 |
6. Средняя величина абсолютного значения 1% прироста ( 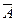 ) ) | 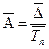 |
Индексы
В статистикепод индексомпонимается относительный показатель, которой выражает соотношение величин какого-либо явления во времени, в пространстве или сравнение фактических данных с любым эталоном (план, прогноз, норматив и т. д.). Он широко применяется для анализа изменений сложных экономических явлений. Под сложными явлениями понимаются те, которые состоят из элементов непосредственно несоизмеримых, не поддающихся простому суммированию (на рынке реализованы: молоко, яйца, рыба, масло и т. п.). С помощью индексов решаются много задач; все их можно привести к двум типам:
а) сравнительная характеристика сложных явлений;
б) разложение сложного явления на его составляющие.
Конкретные индексы различаются между собой по разным признакам:
· степень охвата явления;
· база сравнения;
· вид весов (соизмерителя);
· форма построения;
· характер объекта исследования;
· объект исследования;
· состав явления;
· период исчисления.
Но прежде всего их следует классифицировать по степени охватываемых объектов.
При этом:
- индексы, построенные по широкому кругу разнородных элементов, называются общими (сводными);
- если расчет по части совокупности, то индексы будут групповыми или субиндексами;
- если индексы строятся по отдельным явлениям, то они называются индивидуальными индексами.
Необходимо обратить внимание на агрегатную форму индекса, как на основную, наиболее часто применяющуюся в экономическом анализе, наряду с агрегатными применяются и средние индексы – средний арифметический и средний гармонический.
Краткие указания
Приступая к анализу изменения явлений с помощью индексов, прежде всего необходимо уяснить, изменение какого показателя надо охарактеризовать через изменение цен, то рассчитывается индекс цен Iр, индексируемой величиной является цена Р. При этом следует иметь в виду, что если надо охарактеризовать изменение однородных явлений, то применяют индивидуальные индексы:
Индекс себестоимости 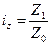 .
.
Индекс физического объема продукции 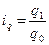 ,
,
а для характеристики сложных, непосредственно несуммируемых явлений – сводные индексы:
цен 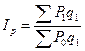 ,
,
физического объема  ,
,
товарооборота 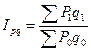 .
.
Определив индекс, который необходимо рассчитать, следует посмотреть, какими исходными данными вы располагаете, и соответственно выбрать форму индекса.
Агрегатной формой индекса пользуются, если известны значения индексируемой величины и их веса, как в отчетном, так и базовом периодах, т. е.
агрегатный индекс себестоимости имеет вид 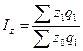 ,
,
производительности труда: 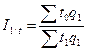 ,
,
затрат: 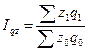 ,
,
трудоемкости: 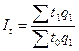 ,
,
массы отработанного времени: 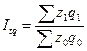 ,
,
удельного расхода топлива: 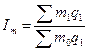 .
.
Средние индексы применяют, если не известны значения отдельных и индексируемых явлений и их весов в отчетном или базовом периодах, но известны и их изменения iq, ix, а также величина явления в отчетном или базовом периодах ∑x1q1, ∑z0q0. При этом, если анализируется изменение объема, то пользуются обычно среднеарифметическим взвешенным индексом, например, среднеарифметическим индексом физического объема:
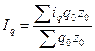 .
.
Если анализируется изменение производных величин средних относительных, то обычно используется среднегармонический индекс себестоимости:
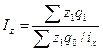 .
.
Если при анализе изменения явления не известны значения индексируемого показателя и их веса, но задано значение факторных показателей, от которых зависит индексируемый анализируемый показатель, расчет индекса ведут исходя из взаимосвязи индексов.
Предварительно необходимо доказать эту взаимосвязь. Например, индекс себестоимости определяет индекс затрат и индекс физического объема. Это выражается следующим образом:
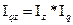 .
.
Это можно доказать
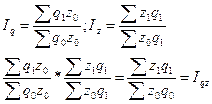
Взаимосвязь индексов дает основание воспользоваться вышеприведенной зависимостью и по двум заданным индексам рассчитывать третий. При анализе изменения средних уровней пользуются индексами постоянного состава, переменного состава и структурных сдвигов.
Например, индекс постоянного состава себестоимости имеет вид
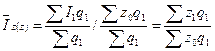 ,
,
индекс структурных сдвигов себестоимости:
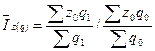 ,
,
индекс переменного состава:
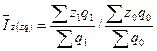 .
.
Выборочное наблюдение
Наиболее совершенным и научно обоснованным способом несплошного наблюдения является выборочное наблюдение.
Выборочное наблюдение при строгом соблюдении условий случайности и достаточно большой численности отобранных единиц репрезентативно (представительно); по результатам изучения определенной части единиц с достаточной для практики степенью точности можно судить о всей совокупности. Однако вычисленные по материалам выборочного наблюдения статистические показатели не будут точно совпадать с соответствующими характеристиками для всей совокупности (генеральной совокупности). Величина этих отклонений называется ошибкой наблюдения, которая складывается из ошибок двоякого рода: ошибки регестрации (точности) и ошибки репрезентативности.
По степени охвата единицисследуемой совокупности различают большие и малые выборки.
По способу формированиявыборочной совокупности различают следующие виды выборочного наблюдения: простая случайная (собственно случайная) выборка, расслоенная (типическая или районированная), серийная, механическая, комбинированная, ступенчатая, многофазная.
Краткие указания
При решении задачи следует прежде всего иметь в виду, что при выборочном наблюдении, поскольку оно не сплошное, всегда имеет место расхождение между генеральными и выборочными статистическими характеристиками 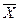 и
и 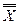 ,
, 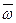 и
и 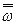 ,
, 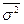 и
и 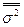 и т. п.
и т. п.
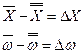
Эту разницу между генеральной и выборочной характеристиками называют ошибкой выборки. Ее величина зависит от числа единиц, отобранных в выборочную совокупность n и дисперсии анализируемого признака 62х, 62n. Чем больше единиц в выборке, тем ошибка выборки меньше, чем больше дисперсия анализируемого признака, тем ошибка больше.
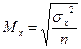 , (1)
, (1)
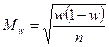 , (2)
, (2)
где Мх, Мw – соответственно ошибка средней и доли;
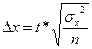 , (3)
, (3)
 , (4)
, (4)
где Dx,Dw – соответственно предельная ошибка средней и доли;
t – коэффициент доверия, функция вероятности ошибки Р выборочного наблюдения.
Таблица значений коэффициентов доверия и ошибки выборки приведена в Приложении.
Зная и понимая вышеприведенные формулы, можно определить все остальные компоненты этих формул. Для облегчения работы в таблицах 3, 4 приведены формулы расчета ошибки Мх, Dх, и численности выборки n при различных способах отбора единиц в выборку.
Следует иметь в виду, что конечная цель выборочного наблюдения состоит в определении генеральной характеристики средней доли на основе расчета выборочных характеристик 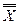 ,
, 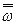 и ошибки выборки Dх, Dw, поскольку между ними существует следующая зависимость:
и ошибки выборки Dх, Dw, поскольку между ними существует следующая зависимость:
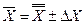 ,
,
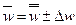 .
.
Т а б л и ц а 3
