Учет (дисконтирование) по сложной ставке процентов

Здесь, также как и в случае простых процентов, будут рассмотрены два вида учета - математический и банковский.

Математический учет. В этом случае решается задача обратная наращению по сложным процентам. Запишем исходную формулу для наращения

S=P(1+i)ⁿ

и решим ее относительно P

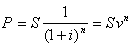, (35)

где

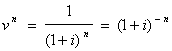(36)

учетный или дисконтный множитель.

Если проценты начисляются m раз в году, то получим

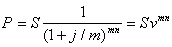, (37)

где

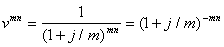(38)

дисконтный множитель.

Величину P, полученную дисконтированием S, называют современной или текущей стоимостью или приведенной величиной S. Суммы P и S эквивалентны в том смысле, что платеж в сумме Sчерез n лет равноценен сумме P, выплачиваемой в настоящий момент.

Разность D=S-P называют дисконтом.

Банковский учет. В этом случае предполагается использование сложной учетной ставки. Дисконтирование по сложной учетной ставке осуществляется по формуле

P=S(1-d_сл)ⁿ, (39)

где d_сл - сложная годовая учетная ставка.

Дисконт в этом случае равен

D=S-P=S-S(1-d_сл)ⁿ=S[1-(1-d_сл)ⁿ]. (40)

При использовании сложной учетной ставки процесс дисконтирования происходит с прогрессирующим замедлением, так как учетная ставка каждый раз применяется к сумме, уменьшенной за предыдущий период на величину дисконта.

Номинальная и эффективная учетные ставки процентов

Номинальная учетная ставка.

В тех случаях, когда дисконтирование применяют m раз в году, используют номинальную учетную ставкуf. Тогда в каждом периоде, равном 1/m части года, дисконтирование осуществляется по сложной учетной ставке f/m. Процесс дисконтирования по этой сложной учетнойm раз в году описывается формулой

P=S(1-f/m)^N, (41)

где N - общее число периодов дисконтирования (N=mn).

Дисконтирование не один, а m раз в году быстрее снижает величину дисконта.

Эффективная учетная ставка. Под эффективной учетной ставкой понимают сложную годовую учетную ставку, эквивалентную (по финансовым результатам) номинальной, применяемой при заданном числе дисконтирований в году m.

В соответствии с определением эффективной учетной ставки найдем ее связь с номинальной из равенства дисконтных множителей

(1-f/m)^mn=(1-d_сл)ⁿ,

из которого следует, что

d_сл=1-(1-f/m)^m. (42)

Отметим, что эффективная учетная ставка всегда меньше номинальной.

Наращение по сложной учетной ставке.

Наращение является обратной задачей для учетных ставок. Формулы наращения по сложным учетным ставкам можно получить, разрешая соответствующие формулы для дисконтирования (39 и 41) относительно S. Получаем

из P=S(1-d_сл)ⁿ

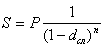, (43)

а из P=S(1-f/m)^N

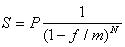. (44)

Пример 11.

Какую сумму следует проставить в векселе, если реально выданная сумма равна 20 млн. руб., срок погашения 2 года. Вексель рассчитывается, исходя из сложной годовой учетной ставки 10%.

Решение.

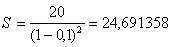млн. руб.

Пример 12.

Решить предыдущую задачу при условии, что наращение по сложной учетной ставке осуществляется не один, а 4 раза в год.

Решение.

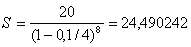млн. руб.

Непрерывные проценты