Расчет срока платежа. Функция КПЕР

Практическое занятие №4

Эта функция вычисляет общее число периодов выплат как для единой суммы вклада (займа), так и для периодических постоянных выплат на основе постоянной процентной ставки. Если платежи производятся несколько раз в год, найденное значение необходимо разделить на число расчетных периодов в году, чтобы найти число лет выплат.

Синтаксис КПЕР(норма, плт, пс, бс, тип).

Функция может применяться в следующих расчетах:

1. Если рассчитывается общее число периодов начисления процентов, необходимых для того, чтобы начальная сумма размером псдостигла указанного будущего значения бс,то формула примет вид

=КПЕР(норма,, пс, бс) (формула 1)

2. Для расчета общего числа периодов, через которое совокупная величина фиксированных периодических выплат составит указанное значение бс,вычисляется аргумент для формулы (2), если эти платежи производятся в начале каждого расчетного периода, или аргумент n формулы (3), если платежи производятся в конце каждого периода. Соответствующий расчет в EXCEL имеет вид:

=КПЕР(норма, плт, , бс, 1)(формула 2)

для выплат в начале периода, и

=КПЕР(норма, плт,, бс)(формула 3)

для выплат в конце периода.

3. При погашении займа размером псравномерными постоянными платежами в конце каждого расчетного периода число периодов, через которое произойдет полное погашение, равно

КПЕР(норма, плт, пс).

Полученное значение можно также использовать как показатель срока окупаемости при анализе инвестиционного проекта. При этом предполагается, что поступление доходов происходит периодически равными величинами в конце или в начале каждого расчетного периода. Рассчитанное значение будет представлять число расчетных периодов, через которое сумма доходов, дисконтированных на момент завершения инвести­ций, будет равна величине инвестиций.

Задача 1

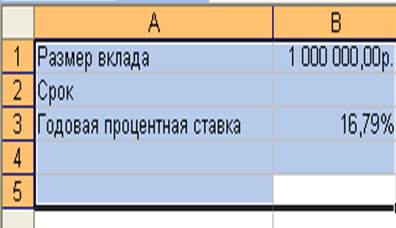
Рассчитать, через сколько лет вклад размером 1 млн. руб. достигнет величины 1 млрд. руб., если годовая ставка процента по вкладу 16.79% и начисление процентов производится ежеквартально.

Решение

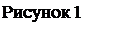1. Откройте табличный редактор Excel и переименуйте Лист1в Расчет функции КПЕР.

2. Подготовьте рабочий лист к выполнению расчетов так, как представлено на рисунке 1.

3. Для ячейки В1 задайте денежный формат;

4. Для ячейки В3 задайте процентный формат

5. Используя функцию КПЕР рассчитаем в ячейке В2 срок в течении которого вклад 1000000 руб. достигнет размера 1 млрд. руб., для этого:

1. Установить курсор в ячейку В2;

2. Зайти в пункт меню Вставка и выбрать раздел Функция…;

3. В открывшемся окне мастера функций в разделе Категория выбрать Финансовые функции;

4. В списке функций выбрать функцию КПЕР;

Расчет ведется по формуле 1. При квартальном начислении процентов размер процента за период равен 16.79%/4. Используем аргументы норма = 16.79%/4, пс = -1000000, бс = 1000000000 функции КПЕР:

=КПЕР(16.79%/4„-1000000,1000000000) = 168 — это число кварталов. Число лет составит 168/4 = 42.

Задача 2

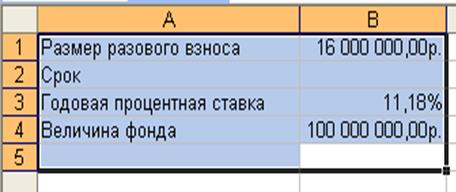
Для обеспечения будущих расходов создается фонд. Средства в фонд поступают в виде постоянной годовой ренты постнумерандо. Размер разового платежа 16 млн. руб. На поступившие взносы начисляется 11.18% годовых. Необходимо определить, когда величина фонда будет равна 100 млн. руб.

Решение

1 Подготовьте рабочий лист к выполнению расчетов так, как представлено на рисунке 2.

2 Для ячейки В1 и В4 задайте денежный формат;

3 Для ячейки В3 задайте процентный формат

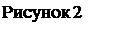4 Используя функцию КПЕР рассчитаем в ячейке В2 срок, в течении которого вклад 16000000 руб. достигнет размера 100 млн. руб., для этого:

a. Установить курсор в ячейку В2;

b. Зайти в пункт меню Вставка и выбрать раздел Функция…;

c. В открывшемся окне мастера функций в разделе Категория выбрать Финансовые функции;

d. В списке функций выбрать функцию КПЕР;

Для решения задачи необходимо вычислить величину и из формулы (3). В EXCEL этот расчет выглядит так:

КПЕР(11.18%, -16000000„1000000000) = 5,

т.е. через 5 лет совокупная величина этих выплат составит 100 млн. руб.

Задания для расчетов

Задача 3

Ожидается, что ежегодные доходы от реализации проекта составят 33 млн. руб. Необходимо рассчитать срок окупаемости проекта, если инвестиции к началу поступления доходов составят 100 млн. руб., а норма дисконтирования 12.11%.

Решение

В задаче требуется определить, через сколько лет текущая стоимость ожидаемых доходов будет равна величине инвестиций. Используем аргументы функции КПЕР пс = -100000000 (значение затрат), выплата= 330000000 (ежегодные поступления), норма= ⁼ 12.11% (норма дисконтирования):

КПЕР(12,11%, 33000000,-100000000) = 4 , то есть срок окупаемости 4 года.

Задача 4

Ссуда размером 66000 тыс. руб., выданная под 36% годовых, погашается обычными ежемесячными платежами по «6630 тыс. руб. Рассчитаем срок погашения ссуды.

Решение

Процентная ставка за месяц составит 36%/12 (аргумент норма).При использовании функции КПЕР ежемесячные выплаты необходимо записать как отрицательные числа (аргумент плт= -6630000), а сумму полученного займа — как положительное число (пс= 66000000). Так как заем полностью погашается, его будущая стоимость равна 0 (аргумент бсможно опустить). Срок, за который произойдет полное погашение займа, равен:

КПЕР(36%/12-6630,66000) = 12 мес. или 1 год.

5 Рассчитайте, через сколько лет обязательные ежемесячные платежи размером 150 тыс. руб. принесут доход в 10 млн.руб.при ставке процента 13.5% годовых.

Ответ: 4.17 года.

6 Рассчитайте, через сколько лет произойдет полное погашение займа размером 500 тыс. руб., если выплаты по 100 тыс.руб. производятся в конце каждого квартала, а ставка процента — 15% годовых.

Ответ: 1.2 года.

7 Рассчитайте, через сколько лет вклад размером 500 тыс. руб. достигнет величины 1 млн. руб. при ежемесячном начислении процентов и ставке 35.18% годовых. Ответ: 2 года.

8 Сравните по сроку окупаемости три варианта инвестиций, которые характеризуются следующими потоками платежей (млн. руб.):

Вариант	Начальные затраты	Ежегодные поступления
А	-240
Б	-290
В	-340

Норма дисконтирования — 12%.

Ответ: срок окупаемости для вариантов А и В — 4 года, для варианта Б — 4.5 года.