Наибольшее значение (100 перцентиль)
Что такое перцентиль
Перцентили — это характеристики набора данных, которые выражают ранги элементов в виде процентов от 0 до 100%, а не в виде чисел, от 1 до n, таким образом, что наименьшему значению соответствует нулевой перцентиль, наибольшему — 100-й перцентиль, медиане — 50-й перцентиль и т.д. Перцентили можно рассматривать как показатели, разбивающие наборы количественных и порядковых данных на определенные части.
Обратите внимание, что перцентиль представляет собой имеющий определенный ранг элемент данных и выражен в тех же единицах, что и единицы набора данных. Например, 60-й перцентиль эффективности продаж может быть равен $385 062 (измерен не в процентах, а в долларах, как и элементы набора данных). Если этот 60-й перцентиль, равный $385 062, характеризует деятельность определенного агента по продажам (например, Мари), то это означает, что приблизительно 60% других агентов имеют результаты ниже, чем у Мари, а 40% агентов имеют более высокие результаты.
Перцентили используют для двух целей.
1. Чтобы показать значение элемента в данных при заданном перцентильном ранге (например, “10-й перцентиль равен $156 293”).
2. Чтобы показать перцентильный ранг значения данного элемента в наборе данных (например, “эффективность продаж агента по сбыту (Джона) составляет $296 994, что соответствует 55-му перцентилю”).
Экстремумы, квартили и блочные диаграммы
Перцентили играют важную роль в качестве опорных характеристик. Чтобы обобщить основные черты распределения, достаточно нескольких значений перцентилей. Так, 50-й перцентиль — это медиана, поскольку 50-й перцентиль находится посередине между наибольшим и наименьшим значениями ряда. Интерес представляют экстремумы - наибольшее и наименьшее значения данных, т.е. 0-й и 100-й перцентили соответственно. Дополняют набор базовых характеристик квартили, определяемые как 25-й и 75-й перцентили.
Удивительно, но статистики до сих пор спорят относительно точного определения квартилей, поскольку их можно вычислять разными способами. Идея квартилей понятна. Квартили — это значения ранжированного ряда, которые находятся на расстоянии одной четвертой на пути от наименьшего или наибольшего значений. Однако эта формулировка не указывает точно, как вычислять квартили. Джон Тьюки, один из создателей практического анализа данных, определяет квартили таким образом.
1. Вычисляем ранг медианы по формуле (1 + n)/2 и отбрасываем дробную часть. Например, при n=13 получаем (1 + 13)/2 = 7. При n=24отбрасываем дробную часть (1 + 24)/2 = 12,5 и получаем 12.
2. Добавляем к полученному значению 1 и делим на 2. Полученное значение представляет собой ранг нижнего квартиля. Например; при n = 13 ранг нижнего квартиля равен (1 + 7)/2=4. При n=24 ранг нижнего квартиля равен (1 + 12)/2 = 6,5, что свидетельствует о необходимости усреднить значения с рангами 6 и 7.
3. Отнимаем полученное значение от (n +1). Результатом будет ранг верхнего
квартиля. Например, при n = 13 получим. (13 + 1)-4 = 10. При n = 24 получаем (1 + 24) - 6,5=18,5, что свидетельствует о необходимости усреднить значения с рангами 18 и 19.
Пять базовых показателей включают:
Наименьшее значение данных (0-й перцентиль),
Нижний квартиль (25 перцентиль),
Медиана (50 перцентиль),
Верхний квартиль (75 перцентиль),
наибольшее значение (100 перцентиль).
Вместе эти характеристики дают достаточно ясное представление об особенностях еще необработанного набора данных. Два экстремума характеризуют размах (диапазон) данных, медиана показывает центр, два квартиля определяют границы, “расположенной в центре половины данных”, а положение медианы относительно квартилей дает грубое представление о наличии или отсутствии асимметрии.
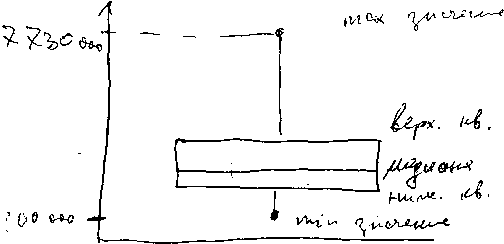
Блочная диаграмма — это изображение всех пяти указанных показателей (рис. 1).
| Min значение |
| Нижний квартиль |
| Верхний квартиль |
| Медиана |
| Наибольшее значение |
Рис. 1. Блочная диаграмма содержит пять базовых показателей одномерного набора данных и позволяет быстро определить характер распределения.
Блочная диаграмма, как и гистограмма, дает визуальное представление о распределении, но использует иной способ графического отображения. Блочная диаграмма не содержит мелких деталей, что позволяет охватить всю картину в целом и сравнивать несколько групп чисел, не вдаваясь в детали каждой из групп. При необходимости подробно рассмотреть форму распределения лучше использовать гистограмму.
Подробная блочная диаграмма — это блочная диаграмма, которая также содержит помеченные метками выбросы (метки также используют для показа экстремальных наблюдений, не являющихся выбросами). Метки выделяют те наблюдения, которые требуют особого внимания. При создании подробной блочной диаграммы выбросыопределяют как те значения данных (если они есть), которые расположены далеко от центра распределения. В частности, большое значение в наборе данных рассматривается как выброс, если оно превышает:
верхний квартиль + 1,5 (верхний квартиль - нижний квартиль).
Малое значение в наборе данных рассматривается как выброс, если оно меньше, чем:
нижний квартиль - 1,5 (верхний квартиль - нижний квартиль).
Так выбросы определяет Тьюки. В дополнение к нанесению на диаграмму выбросов с соответствующими метками можно также отметить экстремальные значения, которые выбросами не являются (по одному с каждой стороны), поскольку часто они также заслуживают особого внимания.
На рис. 4.2.2 для сравнения показаны блочная и подробная блочная диаграммы.
 Пример. Выплаты руководителям
Пример. Выплаты руководителям
Рассмотрим выплаты (заработная плата и премии) руководителям финансовых компаний в 1994 году. Табл. 1 содержит упорядоченный список размеров выплат, их ранги и соответствующие пять характеристик распределения.
Таблица 1. Выплаты руководителям финансовых компаний.
| № | Фирма | Заработная плата и премии, $ | Ранг |
| Equitable * Bear Steams * First Financial Mgmt * Merrill Lynch * Travelers * American Intl. Group Schwab (Charles) Dean Witter Discover American Express Marsh & McLennan Progressive American General Loews Torchmark Household International Aflac Cigna Great Western Financial Transamerica General RE Chubb AON St. Paul CAN Financial Providian Jefferson-Pilot Aetna life & Casualty First USA Salomon Golden West Financial Cincinnati Financial Allstate Block (H&R) Franklin Resources Safeco Equifax Unintrin Berkshire Hathaway | 38-Наиб. значение = 7730000 29-Верхний квартиль=2101000 Медиана=1497500, ранг 19,5 10-Нижний квартиль=1000000 1-Наим. значение = 100000 |
*- это выброс.
Таблица содержит данные о n=38 фирмах, следовательно, медиана (1 497 500) имеет ранг (1+38)/2 = 19,5 и представляет собой среднее значение выплат руководителям фирм Transamerica (ранг 19) и General RE (ранг 20). Нижний квартиль (1 000 000) имеет ранг (1 + 19)/2 = 10 и представляет собой выплаты, полученные в фирме Salomon. Верхний квартиль (2 101 000) имеет ранг (38+1)-10 = 29и представляет собой выплаты в фирме Marsh & McLennan.
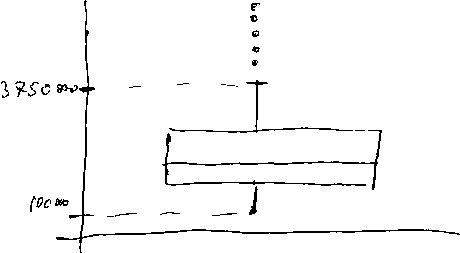
Есть ли среди значений выбросы? Если рассчитать выбросы с использованием квартилей, то выплаты, размер которых превышает 2 101 000+1,5 * (2 101 000 - 1 000 000) =3 752 000, будут выбросами. Таким образом, пять самых высоких выплат (выплаченные фирмами Equitable, Bear Steams, First Financial Mgmt, Merrill Lynch, Travelers) являются выбросами в верхней части. С другой стороны, любые выплат, размер которых меньше, чем 1 000 000 - 1,5 * (2 101 000-1 000000) =- 651 500, также будут выбросами. Поскольку размер наименьшей выплаты равен 100 000, то в нижней части распределения выбросов нет. Блочные диаграммы для этих 38 фирм приведены на рис. 4.2.2. Хотя обычно используют одну диаграмму (вероятно, с большим количеством подробностей), мы для сравнения приводим здесь обе диаграммы.
Одно из преимуществ блочных диаграмм заключается в том, что они позволяют сконцентрировать внимание на основных особенностях нескольких наборов данных одновременно, не отвлекаясь на детали. Рассмотрим выплаты, полученные в 1994 году руководителями крупных банков, предприятий фармацевтической отрасли, коммунальных предприятий и финансовых кампаний). Теперь мы имеем четыре самостоятельных набора данных: по одному одномерному набору данных (набору значений) для каждой из четырех отраслей. Это означает, что для каждой из отраслей можно вычислить пять основных показателей и построить блочную диаграмму. Расположив построенные в одном масштабе блочные диаграммы на одном рисунке (рис.4.2.3), можно легко сравнить типичные размеры выплат руководителям в разных отраслях.
Обратите внимание, насколько информативнее верхний рисунок, содержащий помеченные исключительные значения выплат руководителям отдельных фирм, по сравнению с нижним рисунком, на котором показано только пять базовых показателей. Хотя выше всего оплачиваются руководители некоторых финансовых компаний (выбросы), в целом размеры выплат в этой отрасли, не очень отличаются от выплат руководителям в банковской сфере и в фармацевтической отрасли. Из рисунка также видно, что руководители коммунальных служб, за некоторыми исключениями, оплачиваются ниже, чем в других отраслях.
Какая из диаграмм лучше? Есть смысл тратить время и энергию на построение подробной блочной диаграммы (с показом отдельных выбросов), только если это дает действительно необходимую дополнительную информацию. Стратегически разумно сначала быстро нанести на диаграмму пять базовых показателей, а затем уже решать, стоит ли тратить время и усилия на дополнительные подробности. Конечно, если построение диаграммы выполняется с помощью компьютера, всегда (или почти всегда) следует отдавать предпочтение подробной блочной диаграмме.
