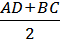Точки, прямые, отрезки.
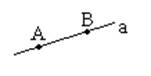 Через любые две точки можно провести прямую, и притом только одну. Прямая а и точки А и В. Через любые две точки можно провести прямую, и притом только одну. Прямая а и точки А и В. | Если две прямые имеют общую точку, то они пересекаются. 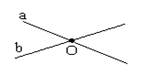 Прямая а и b пересекаются в точке О. Прямая а и b пересекаются в точке О. |
| Две прямые либо имеют только одну общую точку, либо не имеют общих точек. |
Угол.
| Угол – это геометрическая фигура, которая состоит из точки и двух лучей, исходящих из этой точки. |
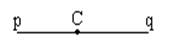 Угол называется развёрнутым, если обе его стороны лежат на одной прямой. Развёрнутый угол = 180º; Угол называется развёрнутым, если обе его стороны лежат на одной прямой. Развёрнутый угол = 180º; | 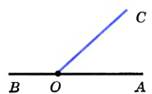 Неразвёрнутый угол < 180º . Неразвёрнутый угол < 180º . |
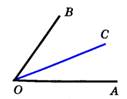 Луч, исходящий из вершины угла и делящий его на два равных угла, называется биссектриса угла. Луч, исходящий из вершины угла и делящий его на два равных угла, называется биссектриса угла. |
| Смежные и вертикальные углы |
Два угла, у которых одна сторона общая, а две другие являются продолжениями одна другой, называются смежными. 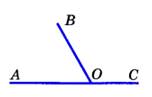 ‹АОВ + ‹ВОС = ‹АОС = 1800 ‹АОВ + ‹ВОС = ‹АОС = 1800 | Два угла ,называются вертикальными , если стороны одного угла являются продолжениями сторон другого. 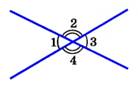 1 и 3, 2 и 4 – вертикальные углы. 1 и 3, 2 и 4 – вертикальные углы. |
Треугольники.
Треугольник – геометрическая фигура, которая состоит из 3 точек, не лежащих на одной прямой, соединённых отрезками. 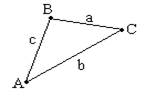 РАВС = АВ+ВС+СА. РАВС = АВ+ВС+СА. |
Теорема:Если 2 стороны и угол между ними 1-го треугольника соответственно равны 2 сторонам и углу между ними другого треугольника, то треугольники равны. 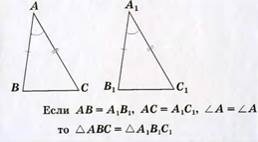 | Теорема: Из точки, не лежа- щей на прямой, можно провести перпендикуляр к этой, и притом только один. 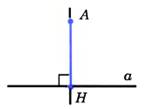 АН ┴ а АН ┴ а |
Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника. 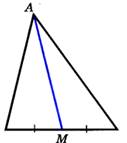 АМ - медиана АМ - медиана | Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны, называется биссектрисой треугольника. 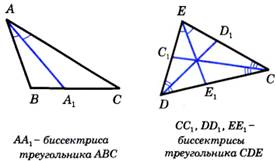 |
Перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону, называется высотой треугольника. 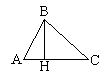 ВН - высота ∆АВС. ВН - высота ∆АВС. |
Треугольник, у которого 2 стороны равны, называется равнобедренным. 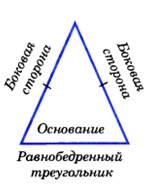 | Теорема:В равнобедренном треугольнике углы при основании равны. 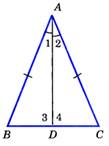 ‹В = ‹С ‹В = ‹С |
Теорема:В равнобедренном треугольнике биссектриса, проведённая к основанию, является медианой и высотой. 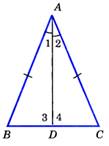 | 1. Высота равнобедренного треугольника, проведённая к основанию, является медианой и биссектрисой. 2. Медиана, проведённая к основанию, является высотой и биссектрисой. |
Теорема: Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то треугольники равны. 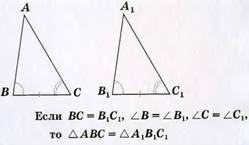 | Теорема: Если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то такие треугольники равны. 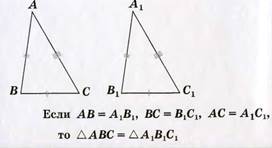 |
| Определение: Окружность называется геометрическая фигура, состоящая из всех точек, расположенных на заданном расстоянии от данной точки. |
Параллельные прямые
Определение: Две прямые на плоскости параллельны, если они не пересекаются. 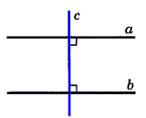 | Прямая с называется секущей по отношению к прямым а и b, если она пересекает их в двух точках. 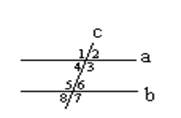 Накрест лежащие – 3 и 5, 4 и 6. Односторонние – 4 и 5, 3 и 6. Соответственные – 1 и 5, 4 и 8,2 и 6, 3 и 7. Накрест лежащие – 3 и 5, 4 и 6. Односторонние – 4 и 5, 3 и 6. Соответственные – 1 и 5, 4 и 8,2 и 6, 3 и 7. |
| Теорема: Если при пересечении 2 прямых секущей накрест лежащие углы равны, то прямые параллельны. | Теорема: Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны. |
| Теорема: Если при пересечении двух прямых секущей сумма односторонних углов равна 180º, то прямые параллельны. | Теорема:Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны. |
| Теорема:Если две параллельные прямые пересечены секущей, то соответственные углы равны. | Теорема: Если две прямые пересечены секущей, то сумма односторонних углов равна 180º. |
Соотношения между сторонами
и углами треугольника.
| Теорема:Сумма углов треугольника = 180º. | Теорема: В треугольнике против большей стороны лежит больший угол, против большего угла лежит большая сторона. |
Сторона прямоугольного треугольника, лежащая против прямого угла, называется гипотенузой, а две другие стороны – катетами. 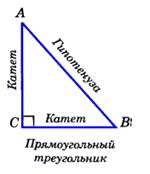 |
| 1.В прямоугольном треугольнике гипотенуза больше катета. 2.Если два угла треугольника равны, то треугольник – равнобедренный. | Теорема: Каждая сторона треугольника меньше суммы двух других сторон. |
| Некоторые свойства прямоугольных треугольников |
1.Сумма двух острых углов прямоугольного треугольника = 90º. 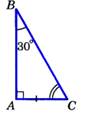 | 2. Катет прямоугольного треуг-ка, лежащий против угла в 30º, равен половине гипотенузы. 3. Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета, равен 30º. |
| Теорема: Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого, то такие треугольники равны | Теорема: Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого, то такие треугольники равны. |
Многоугольники.
| Сумма углов выпуклого n-угольника = (n-2)180º. |
Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны. 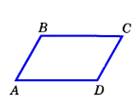 |
Свойства: 10. В параллелограмме противоположные стороны равны и противоположные углы равны. 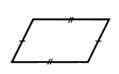 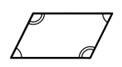 20. Диагонали параллелограмма точ- кой пересечения делятся пополам. 20. Диагонали параллелограмма точ- кой пересечения делятся пополам. 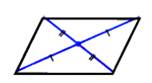 | Признаки: 10. . Если в 4-угольнике 2 стороны равны и параллельны, то этот 4-угольник – параллелограмм. 20. Если в 4-угольнике противопо- ложные стороны попарно равны, то этот 4-угольник – параллелограмм. 30. Если в 4-угольнике диагональю пересекаются и точкой пересечения делятся пополам, то этот 4-угольник – параллелограмм. |
Трапецией называется 4-угольник, у которого 2 стороны параллельны, а 2 другие стороны не параллельны. 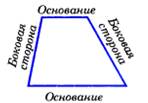 |
Трапецией называется равнобедренной, если ее боковые стороны равны. 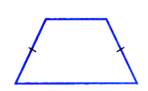 Свойства равнобедренной трапеции: 1. ‹А = ‹Д, ‹В = ‹С 2. АС = ВД 3. ∆АВМ = ∆ДСМ Свойства равнобедренной трапеции: 1. ‹А = ‹Д, ‹В = ‹С 2. АС = ВД 3. ∆АВМ = ∆ДСМ | Ромбом называется параллело-грамм, у которого все стороны равны. 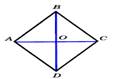 Свойство: Диагонали ромба взаимно перпендикулярны и делят его углы пополам. Свойство: Диагонали ромба взаимно перпендикулярны и делят его углы пополам. |
Прямоугольником называется параллелограмм, у которого все углы прямые. 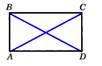 Свойства: 1. Диагонали прямоугольника равны. 2.Если в параллелограмме диагонали равны,то этот пареллелограмм- прямоугольник. Свойства: 1. Диагонали прямоугольника равны. 2.Если в параллелограмме диагонали равны,то этот пареллелограмм- прямоугольник. | Квадратом называется прямо- угольник, у которого все стороны равны. 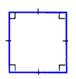 Свойства: 1.Все углы квадрата прямые. 2.Диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам. Свойства: 1.Все углы квадрата прямые. 2.Диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам. |
Площадь.
| 1.Равные многоугольники имеют равные S. 2.S квадрата равна квадрату его стороны. 3. Если многоугольник составлен из нескольких многоугольников, то его S = сумме площадей этих многоугольников. | Теорема: S прямоугольника равен произведению его смежных сторон. 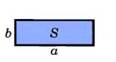 S = a * b S = a * b |
Теорема: S параллелограмма равен произведению его основания на высоту. 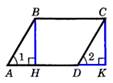 S = AD *BH S = AD *BH | Теорема: S треугольника равен произведению его основание навысоту. 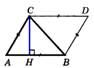 S = ½ АВ*СН S = ½ АВ*СН |
S прямоугольного треугольника = 1/2 произведения его катетов. Формула Герона: 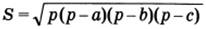 , где р =1/2 (а + b + c)- полупериметр треугольника. , где р =1/2 (а + b + c)- полупериметр треугольника. | Теорема: S трапеции = про- изведению полу суммы её оснований на высоту. 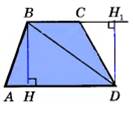 |
Теорема: (Пифагора) В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. 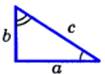 c2=a2 + b2 c2=a2 + b2 | Теорема: Если квадрат 1ой стороны треугольника = сумме квадратов 2 других сторон, то треугольник прямоугольный. |
Подобные треугольники.
Определение: два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорционально сходственны сторонам другого. 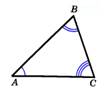 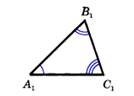 АВ и А1В1, ВС и В1С1 , СА и С1А1 –сходственные стороны АВ и А1В1, ВС и В1С1 , СА и С1А1 –сходственные стороны |
| Теорема: Отношение S 2ух подобных треугольников равен квадрату коэффициента подобия. | |
| Признаки подобия треугольников |
Первый признак Теорема: Если два угла одного треугольника соответственно равны двум углам другого, то такие 3-угольники подобны. 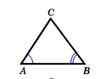 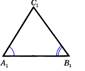 | Второй признак Теорема: Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключённые между этими сторонами, равны, то такие треугольники подобны. |
Третий признак Теорема: Если три стороны одного треугольника пропорциональ-ны трём сторонам другого, то такие треугольники подобны. 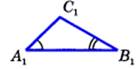 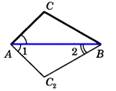 | Теорема: Средняя линия параллельна одной из его сторон и равна ½ этой стороны. 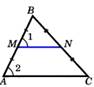 MN = ½ AC MN = ½ AC |
Утверждение: Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное для отрезков, на которое делится гипотенуза этой высотой. 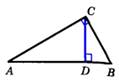 CD = CD = 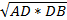 | Утверждение: Катет прямоугольного треугольника есть среднее пропорциональное для гипотенузы и отрезка гипотенузы, заключенного между катетом и высотой, проведенной из вершины прямого угла. 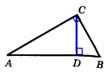 AC = AC = 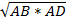 |
| Соотношения между сторонами и углами прямоугольного треугольника |
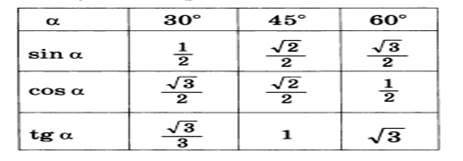
sin острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе. 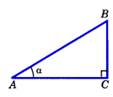 sin A = sin A = 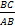 | cos острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе. 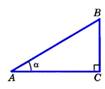 cos A = cos A = 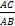 |
tg острого угла прямоугольного треугольника называетсяотношение противолежащего катета к прилежащему. 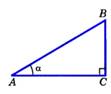 tg A = tg A = 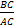 | tg угла = отношению sin к cos этого угла: tg = sin/ cos. Основное тригонометрическое тождество: sin2α + cos2α=1. |
Окружность.
Если расстояние от центра окруж ности до прямой < радиуса, то пря мая и окружность имеют 2 общие точки. Прямая является секущей. 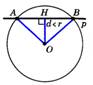 | Если расстояние от центра окруж- ности до прямой = радиуса, то пря- мая и окружность имеют 2 общие точки. Прямая является касательной 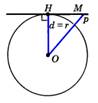 |
Если расстояние от центра окруж- ности до прямой > радиуса, то пря мая и окружность не имеют общих точек. 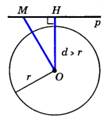 | Теорема: Касательная к окруж- ности перпендикулярна к r, прове- дённому в точку касания. 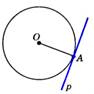 |
Свойство: Отрезки касательных к окружности, проведённые из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности. 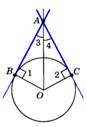 АВ = АС, ‹3 = ‹4 АВ = АС, ‹3 = ‹4 | Теорема: Если прямая проходит через конец r, лежащий на окруж- ности, и перпендикулярна к этому r, то она является касательной. |
| Градусная мера дуги окружности |
Если дуга АВ окружности с центром О меньше полуокружности или является полуокружностью, то её градусная мера считается равной градусной мере центрального угла АОВ. 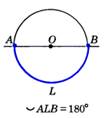 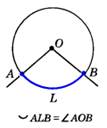 | Если же дуга АВ больше полуокружности, то её градусная мера считается = 360°–<АОВ. 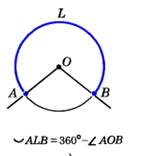 |
| Сумма градусных мер двух дуг окружности с общими концами равна 360°. |
Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным углом. 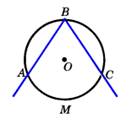 |
Теорема: Вписанный угол измеряя- ется ½ дуги, на которую он опирается. 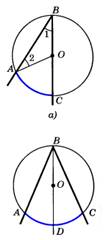 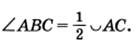 | Следствие 1: Вписанные углы, опирающиеся на 1 и ту же дугу, равны. 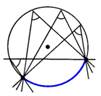 Следствие 2: Вписанный угол, опирающийся на полуокружность- прямой. Следствие 2: Вписанный угол, опирающийся на полуокружность- прямой. 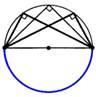 |
Теорема: Если 2 хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды. 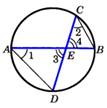 АЕ* ВЕ = СЕ* DE АЕ* ВЕ = СЕ* DE | Теорема: Каждая точка бисс-ектрисы неразвёрнутого угла равноудалена от его сторон. Обратно: Каждая точка, лежащая внутри угла и равноудалённая от сторон угла, лежит на его биссектрисе. 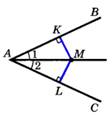 MK = ML MK = ML |
Биссектрисы треугольника пересекаются в одной точке. 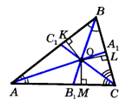 | Серединным перпендикуляром к отрезку называется прямая, проходящая через середину отрезка и перпендикулярная к нему. 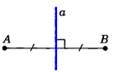 |
| Теорема: Каждая точка се- рединного перпендикуляра к отрезку равноудалена от концов этого отрезка. Обратно: Каждая точка, равноудалённая от концов отрез- ка, лежит на серединном перпен- дикуляре к нему. Серединные перпендикуляры к сторо- нам треугольника пересекаются в одной точке. | Теорема: Высоты треугольника (или их продолжения) пересекаются в одной точке. 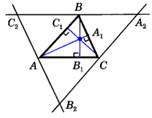 |
| Вписанная и описанная окружности |
Определение: если все стороны многоугольника касаются окружности, то окружность называется вписанной в многоугольник, а многоугольник – описанным около этой окружности. 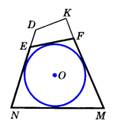 |
Теорема: в любой треугольник можно вписать окружность. 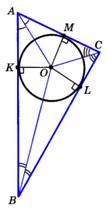 | Замечания: 1. В 3-угольник можно вписать только одну окружность. 2. В отличие от треугольника не во всякий четырехугольник можно вписать окружность.  |
Свойства: В любом описанном четырехугольнике суммы противоположных сторон равны. 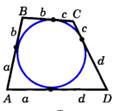 АВ + CD=a + b +c + d, DC +AD=a + b +c + d, AB + CD = BC + AD АВ + CD=a + b +c + d, DC +AD=a + b +c + d, AB + CD = BC + AD | Теорема: Около любого треугольника можно описать окружность. 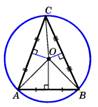 |
Свойства: В любом вписанном 4-угольнике сумма противоположных углов равна 180°. 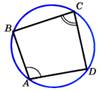 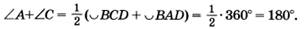 Обратное: Если сумма противоположных углов 4-угольника = 180°, то около него можно описать окружность. Обратное: Если сумма противоположных углов 4-угольника = 180°, то около него можно описать окружность. |
Векторы.
Определение: Отрезок, для которого указано, какая из его граничных точек считается началом, а какая – концом, называется направленным отрезкомиливектором. 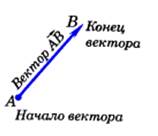 | Нулевые векторы называются коллинеарными, если они лежат либо на одной прямой, либо на параллельных прямых; нулевой вектор считается коллинеарным любому вектору. 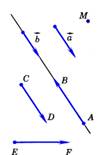 На рисунке векторы На рисунке векторы 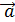 , , 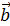 , , 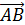 , , 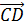 , , 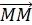 (вектор (вектор 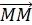 нулевой) колли- неарны, а векторы нулевой) колли- неарны, а векторы 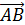 и и 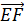 , a также , a также 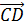 и и 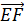 не коллинеарны. не коллинеарны. |
Если 2 вектора направлены одинаково, то эти векторы – сонаправлены. Обозначается : :  ↑↑ ↑↑  Если 2 вектора направлены противоположно, то они противоположно направлены. Обозначается: : Если 2 вектора направлены противоположно, то они противоположно направлены. Обозначается: :  ↑↓ ↑↓  | Определение: Векторы, называются равными, если они сонаправлены и их длины равны. Обозначается:  = =  От любой точки М можно отложить вектор, равный данному вектору От любой точки М можно отложить вектор, равный данному вектору  , и притом только один. , и притом только один. |
Теорема: для любых векторов:  , ,  , , 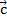 справедливы равенства: 1. справедливы равенства: 1.  + + 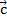 = = 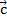 + +  (переместительный закон); 2. ( (переместительный закон); 2. (  + +  ) + ) + 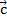 = =  + ( + ( 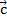 + +  ) (сочетательный закон). ) (сочетательный закон). | Теорема: Для любых векторов  и и  справедливо равенство справедливо равенство  – –  = =  + (- + (-  ). ). 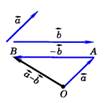 |
· Произведение любого вектора на число нуль есть нулевой вектор. · Для любого числа k и любого вектора  векторы векторы  и k и k  коллинеарны. коллинеарны. | Для любых чисел k, l и любых векторов  , ,  справедливы равенства: 10.(k*l) справедливы равенства: 10.(k*l)  =k(l* =k(l*  ) (сочетательный закон) 20.(k + l) ) (сочетательный закон) 20.(k + l)  =k =k  + l + l  (первый распределительный закон) 30 k( (первый распределительный закон) 30 k(  + +  ) = k ) = k  + k + k  ) (второй распределительный закон) ) (второй распределительный закон) |
Теорема: Средняя линия трапеции параллельна основаниям и равна их полусумме. 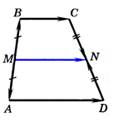 MN = MN = 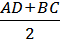 |
Метод координат.
Наши рекомендации
 Через любые две точки можно провести прямую, и притом только одну. Прямая а и точки А и В.
Через любые две точки можно провести прямую, и притом только одну. Прямая а и точки А и В.  Прямая а и b пересекаются в точке О.
Прямая а и b пересекаются в точке О.  Угол называется развёрнутым, если обе его стороны лежат на одной прямой. Развёрнутый угол = 180º;
Угол называется развёрнутым, если обе его стороны лежат на одной прямой. Развёрнутый угол = 180º;  Неразвёрнутый угол < 180º .
Неразвёрнутый угол < 180º .  Луч, исходящий из вершины угла и делящий его на два равных угла, называется биссектриса угла.
Луч, исходящий из вершины угла и делящий его на два равных угла, называется биссектриса угла.  ‹АОВ + ‹ВОС = ‹АОС = 1800
‹АОВ + ‹ВОС = ‹АОС = 1800  1 и 3, 2 и 4 – вертикальные углы.
1 и 3, 2 и 4 – вертикальные углы.  РАВС = АВ+ВС+СА.
РАВС = АВ+ВС+СА. 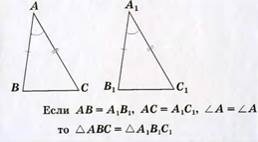
 АН ┴ а
АН ┴ а  АМ - медиана
АМ - медиана 
 ВН - высота ∆АВС.
ВН - высота ∆АВС. 
 ‹В = ‹С
‹В = ‹С 
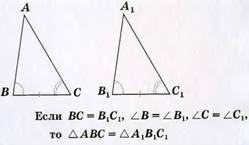
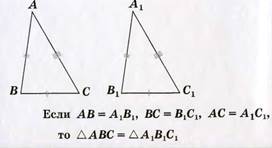

 Накрест лежащие – 3 и 5, 4 и 6. Односторонние – 4 и 5, 3 и 6. Соответственные – 1 и 5, 4 и 8,2 и 6, 3 и 7.
Накрест лежащие – 3 и 5, 4 и 6. Односторонние – 4 и 5, 3 и 6. Соответственные – 1 и 5, 4 и 8,2 и 6, 3 и 7. 



 20. Диагонали параллелограмма точ- кой пересечения делятся пополам.
20. Диагонали параллелограмма точ- кой пересечения делятся пополам. 

 Свойства равнобедренной трапеции: 1. ‹А = ‹Д, ‹В = ‹С 2. АС = ВД 3. ∆АВМ = ∆ДСМ
Свойства равнобедренной трапеции: 1. ‹А = ‹Д, ‹В = ‹С 2. АС = ВД 3. ∆АВМ = ∆ДСМ  Свойство: Диагонали ромба взаимно перпендикулярны и делят его углы пополам.
Свойство: Диагонали ромба взаимно перпендикулярны и делят его углы пополам.  Свойства: 1. Диагонали прямоугольника равны. 2.Если в параллелограмме диагонали равны,то этот пареллелограмм- прямоугольник.
Свойства: 1. Диагонали прямоугольника равны. 2.Если в параллелограмме диагонали равны,то этот пареллелограмм- прямоугольник.  Свойства: 1.Все углы квадрата прямые. 2.Диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам.
Свойства: 1.Все углы квадрата прямые. 2.Диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам.  S = a * b
S = a * b  S = AD *BH
S = AD *BH  S = ½ АВ*СН
S = ½ АВ*СН 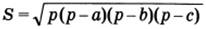 , где р =1/2 (а + b + c)- полупериметр треугольника.
, где р =1/2 (а + b + c)- полупериметр треугольника. 
 c2=a2 + b2
c2=a2 + b2 
 АВ и А1В1, ВС и В1С1 , СА и С1А1 –сходственные стороны
АВ и А1В1, ВС и В1С1 , СА и С1А1 –сходственные стороны 



 MN = ½ AC
MN = ½ AC  CD =
CD = 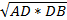
 AC =
AC = 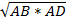
 sin A =
sin A = 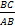
 cos A =
cos A = 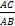
 tg A =
tg A = 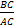





 АВ = АС, ‹3 = ‹4
АВ = АС, ‹3 = ‹4 




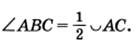
 Следствие 2: Вписанный угол, опирающийся на полуокружность- прямой.
Следствие 2: Вписанный угол, опирающийся на полуокружность- прямой. 
 АЕ* ВЕ = СЕ* DE
АЕ* ВЕ = СЕ* DE  MK = ML
MK = ML 





 АВ + CD=a + b +c + d, DC +AD=a + b +c + d, AB + CD = BC + AD
АВ + CD=a + b +c + d, DC +AD=a + b +c + d, AB + CD = BC + AD 

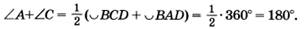 Обратное: Если сумма противоположных углов 4-угольника = 180°, то около него можно описать окружность.
Обратное: Если сумма противоположных углов 4-угольника = 180°, то около него можно описать окружность. 
 На рисунке векторы
На рисунке векторы 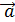 ,
, 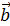 ,
, 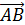 ,
, 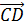 ,
, 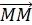 (вектор
(вектор 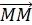 нулевой) колли- неарны, а векторы
нулевой) колли- неарны, а векторы 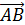 и
и 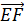 , a также
, a также 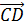 и
и 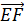 не коллинеарны.
не коллинеарны.  ↑↑
↑↑  Если 2 вектора направлены противоположно, то они противоположно направлены. Обозначается: :
Если 2 вектора направлены противоположно, то они противоположно направлены. Обозначается: :  ↑↓
↑↓ 
 =
=  От любой точки М можно отложить вектор, равный данному вектору
От любой точки М можно отложить вектор, равный данному вектору  , и притом только один.
, и притом только один.  ,
,  ,
, 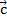 справедливы равенства: 1.
справедливы равенства: 1.  +
+ 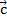 =
= 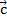 +
+  (переместительный закон); 2. (
(переместительный закон); 2. (  +
+  ) +
) + 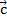 =
=  + (
+ ( 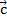 +
+  ) (сочетательный закон).
) (сочетательный закон).  и
и  справедливо равенство
справедливо равенство  –
–  =
=  + (-
+ (-  ).
). 
 векторы
векторы  и k
и k  коллинеарны.
коллинеарны.  ,
,  справедливы равенства: 10.(k*l)
справедливы равенства: 10.(k*l)  =k(l*
=k(l*  ) (сочетательный закон) 20.(k + l)
) (сочетательный закон) 20.(k + l)  =k
=k  + l
+ l  (первый распределительный закон) 30 k(
(первый распределительный закон) 30 k(  +
+  ) = k
) = k  + k
+ k  ) (второй распределительный закон)
) (второй распределительный закон)  MN =
MN =