Аналитическое сложение и вычитание двух векторов

Выберем декартову систему координат 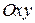. В случае плоской задачи разложение векторов на их проекции (в одной и той же системе координат) позволяет легко сложить (вычесть) векторы аналитически.

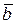Пусть заданы два вектора и (рис. 10.5, а), и пусть нам известны разложения двух векторов на их проекции:

;

;

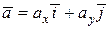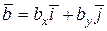Или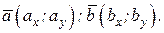

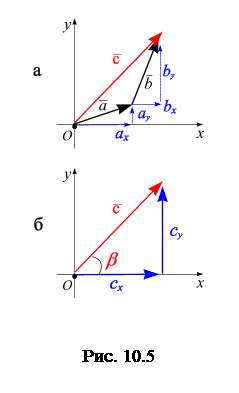Из графического суммирования хорошо видно, что проекции результирующего вектора равны, рис. 10.5, а:

,

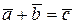здесь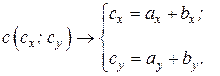

Модуль вектора вычисляется по теореме Пифагора, рис. 10.5, б:

,

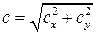а направление сектора 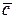вычисляется по направляющему косинусу:

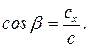
Разность векторов 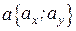и 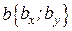можно вычислить, воспользовавшись следующими формулами:

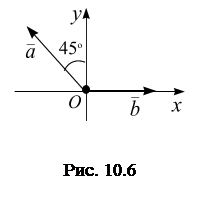
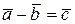, здесь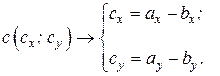

Пример 10.1.Заданы два вектора и 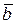: 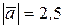, , 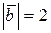направления векторов относительно оси 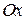показаны на рис. 10.6. Сложить аналитически заданные векторы.

Решение. Совместим прямоугольную систему координат 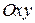с точкой пересечения линий действий заданных векторов, рис. 10.7, а.

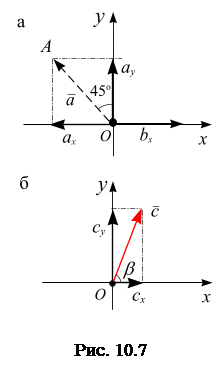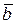Спроецируем векторы и на декартовые оси координат 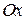и ,

Имеем:

,

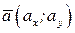здесь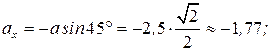

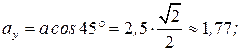
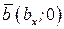, здесь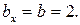

Итак, имеем

,

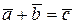здесь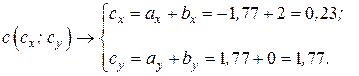

Модуль вектора 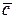вычислим по теореме Пифагора, рис. 10.7, б:

,

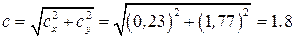а направление сектора 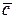вычисляется по направляющему косинусу:

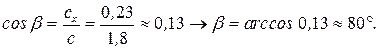
Результаты вычислений совпадают с результатами, полученными геометрическим построением векторов в примере 9.2.

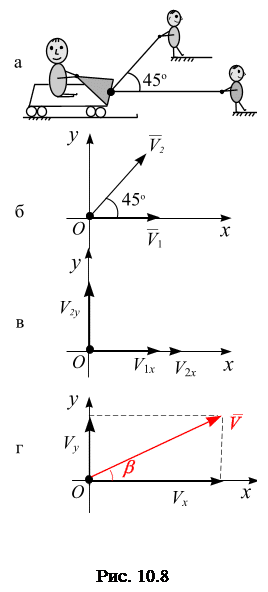Пример 10.2.Два мальчикакатают на тележке третьего мальчика. Первый мальчик катит тележку по горизонтали со скоростью 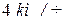, второй – под углом 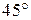к горизонту со скоростью 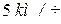(рис. 10.8, а). Вычислить аналитически направление движения тележки.

Решение.Совместим прямоугольную систему координат 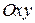с точкой пересечения линий действий заданных векторов, рис. 10.8, б.

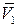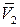Спроецируем векторы и на декартовые оси координат 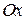и 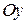, рис. 10.8, в:

Имеем:

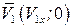, здесь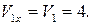

,

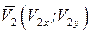здесь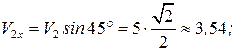

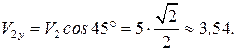
Итак,

,

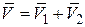здесь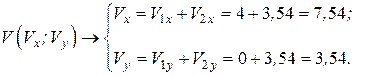

Модуль вектора 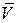вычислим по теореме Пифагора, рис. 10.8, г:

,

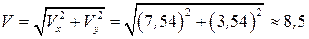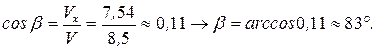а направление сектора 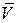вычисляется по направляющему косинусу:

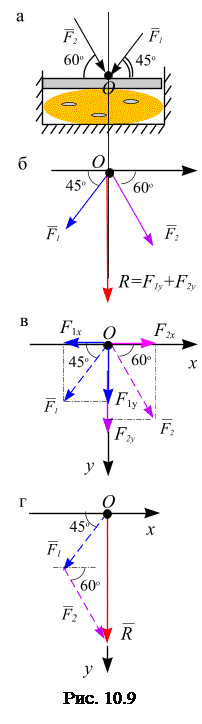
Пример 10.3.На пресс, сжимающий головку сыра, в точке О приложены две силы 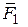и 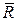(рис. 10.9, а). Вычислить модуль равнодействующей силы 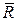, сжимающей головку сыра, если вектор силы 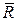направлен вертикально. Дано: 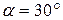, , 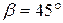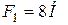. Вычислить: 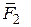и .

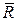Решение. Совместим прямоугольную систему координат 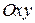с точкой пересечения линий действий заданных векторов,
рис. 10.9, б.

Спроецируем векторы 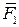и 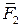на ось 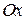, рис. 10.9, в:

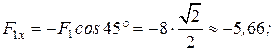
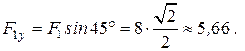
Так как по условию задачи равнодействующая направлена вертикально, то

, , ,

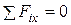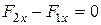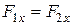следовательно,

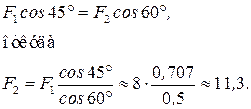
Спроецируем векторы 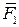и 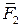на ось :

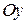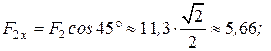
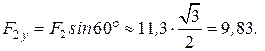
Модуль равнодействующей равен:

.

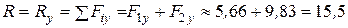Сделаем проверку, построим силовой треугольник, рис. 10.9, г.

Аналитическое сложение трех векторов

Пусть заданы три вектора , 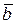и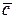
(рис. 10.10), и пусть нам известны разложения трех векторов на их проекции:

; ; .

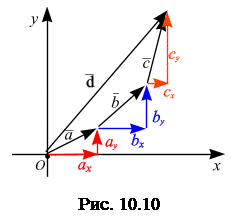
Из графического суммирования хорошо видно, что проекции результирующего вектора

,

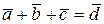Здесь

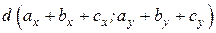
Разность векторов 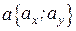, 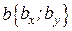и 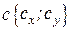можно вычислить, воспользовавшись следующими формулами:

,

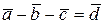здесь

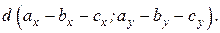
Пример 10.4. Вычислить равнодействующую системы сходящихся сил 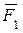, , 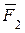, 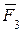приложенных в точку О (рис. 10.11), аналитически, если .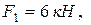

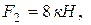
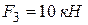Решение. Совместим прямоугольную систему координат 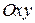с точкой пересечения линий действия заданных векторов.

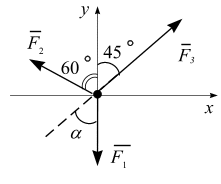Рис. 10.11

Вычислим проекции заданных векторов на оси :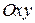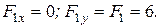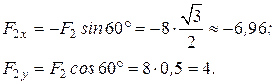

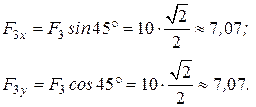
Имеем:

, .

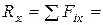
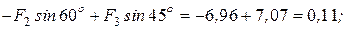
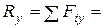
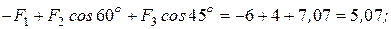
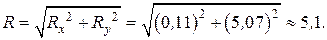
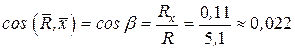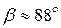Радиус-вектор

Радиус-вектор вводится для описания движений любого объекта.

Выберем неподвижную точку 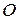и проведем через нее произвольно ось 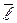. Тогда положение точки на траектории, например 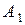, можно определить расстояние между точкой 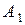и точкой О, а также 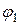. Можно сказать, что величина и направление вектора 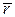изменяюся вместе с изменением абсолютного времени, т.е. скалярного параметра 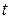. Изменение длины фиксируетсямодулем вектора, а направление – углом 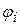. Функция 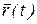называется радиус–вектором скалярного аргумента
(рис. 10.13) и обозначается.

.

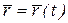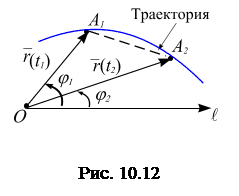
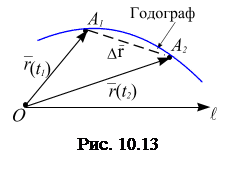Пусть точка движется по траектории
(рис. 10.13). Ее положение в момент времени 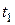определяется вектором 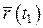, а в момент времени 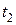– 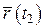. Тогда смешение точки за время 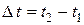определяется разностью

.

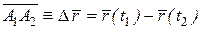При изменении параметра 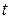конец вектора 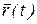опишет некоторую кривую, называемую, называемую годографом (записыватель пути) вектора, т. е. траекторию.

Радиус–вектор 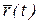можно разложить по базисным векторам 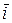, , 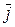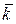прямоугольной пространственной системы координат (рис. 10.14):

,

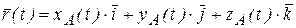причем компоненты 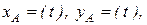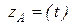являются координатами точки А в прямоугольной системе координат.

Если t означает время, то 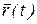фиксирует положение материальной точки в пространстве в любой момент времени, т.е. характеризует движение материальной точки, а годограф радиус-вектора соответствует траектории движения точки.

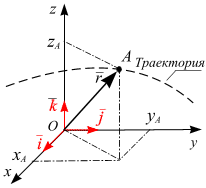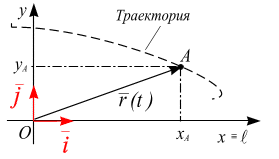Рис. 10.14	Рис. 10.15

Пусть точка движется в плоскости 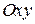. Совместим с точкой 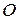начало плоской декартовой системы, а ось 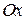с осью 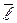(рис. 10.15). В плоской декартовой системе координат радиус–вектор 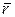раскладывается по базисным векторам 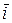, 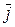так

.

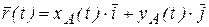Причем, компоненты

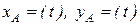
являются координатами точки А в прямоугольной системе координат.