Упражнения для самостоятельной работы. 98.Найти нули функции и определить их порядки:
98.Найти нули функции и определить их порядки:
а) 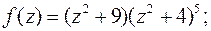 б)
б) 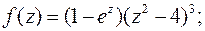
в) 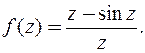
99. Найти изолированные особые точки функции и определить их характер:
а) 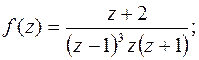 б)
б) 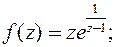
в) 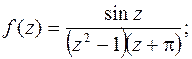 г)
г) 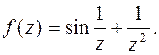
100. Выяснить характер особой 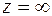 для функций
для функций
а) 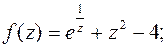 б)
б) 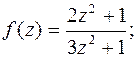
в) 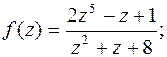 г)
г) 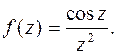
ВЫЧЕТЫ И ИХ ПРИМЕНЕНИЕ К ВЫЧИСЛЕНИЮ
КОНТУРНЫХ ИНТЕГРАЛОВ
Вычет функции и его вычисление
Пусть 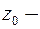 конечная изолированная особая точка однозначной функции
конечная изолированная особая точка однозначной функции 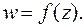 Вычетом функции
Вычетом функции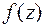 относительно точки
относительно точки 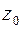 называется число, обозначаемое символом
называется число, обозначаемое символом 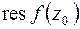 и определяемое равенством
и определяемое равенством
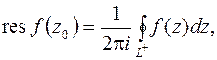 (8.1)
(8.1)
где 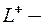 положительно ориентированный замкнутый контур, лежащий в области аналитичности
положительно ориентированный замкнутый контур, лежащий в области аналитичности  и содержащий внутри себя одну особую точку
и содержащий внутри себя одну особую точку 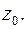 При обходе контура
При обходе контура 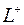 особая точка
особая точка  остается слева.
остается слева.
Из определения следует, что вычет функции равен коэффициенту 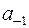 при
при 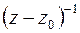 в лорановском разложении
в лорановском разложении  в окрестности точки
в окрестности точки 
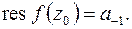 (8.2)
(8.2)
Приведем формулы для вычета в полюсах функции, позволяющие избежать разложения функции в ряд Лорана – процесс в общем случае громоздкий.
Если 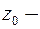 простой полюс функции
простой полюс функции  , то
, то
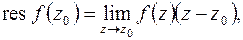 (8.3)
(8.3)
причем если  представима в виде отношения двух аналитических в точке
представима в виде отношения двух аналитических в точке  функций
функций 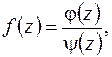 где
где 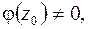
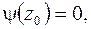
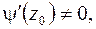 то
то
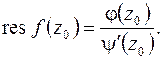 (8.4)
(8.4)
Если 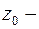 полюс
полюс 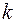 -го порядка
-го порядка 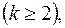 то
то
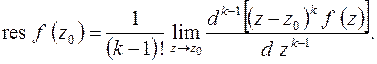 (8.5)
(8.5)
Для устранимой особой точки 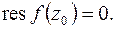 Для нахождения вычета относительно существенно особой точки необходимо найти коэффициент
Для нахождения вычета относительно существенно особой точки необходимо найти коэффициент 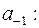
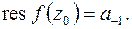
В некоторых случаях находим применение понятие вычета функции относительно бесконечно удаленной точки.
Пусть  аналитична в некоторой окрестности точки
аналитична в некоторой окрестности точки 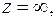 кроме, может быть, самой бесконечно удаленной точки. Вычетом функции
кроме, может быть, самой бесконечно удаленной точки. Вычетом функции  относительно бесконечно удаленной точки
относительно бесконечно удаленной точки 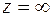 называют величину
называют величину
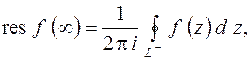 (8.6)
(8.6)
где 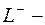 отрицательно ориентированный замкнутый контур, принадлежащий области
отрицательно ориентированный замкнутый контур, принадлежащий области 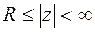 аналитичности функции. При обходе контура
аналитичности функции. При обходе контура 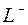
 бесконечно удаленная точка
бесконечно удаленная точка 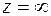 остается слева.
остается слева.
Из определения следует, что вычет относительно 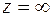 равен коэффициенту при
равен коэффициенту при 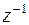 в лорановском разложении
в лорановском разложении  в окрестности
в окрестности 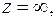 взятому с противоположным знаком:
взятому с противоположным знаком:
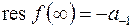 (8.7)
(8.7)
Между утверждениями (8.7) и (8.2), несмотря на их внешнее сходство, имеется существенное различие. Дело в том, что в разложении Лорана в окрестности точки 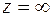 член
член 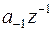 принадлежит правильной (а не главной) части ряда, и
принадлежит правильной (а не главной) части ряда, и 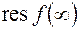 может быть отличным от нуля и тогда, когда
может быть отличным от нуля и тогда, когда  аналитична в бесконечности.
аналитична в бесконечности.
Теоремы о вычетах и их применение к вычислению
Контурных интегралов
Теорема 1. (Основная теорема Коши о вычетах).Если функция  аналитична в области
аналитична в области 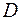 , за исключением изолированных особых точек
, за исключением изолированных особых точек 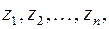 то для любого замкнутого контура
то для любого замкнутого контура 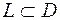 , охватывающего эти точки
, охватывающего эти точки
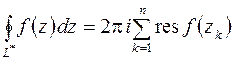 . (8.8)
. (8.8)
Основная теорема о вычетах имеет важное значение для приложений. Она позволяет вычислять интегралы по закнутому контуру от функции комплексного переменного, не прибегая к первообразным или криволинейным интегралам. С помощью вычетов вычисляются определенные и несобственные интегралы от функций действительного переменного. При вычислении некоторых интегралов удобно пользоваться теоремой о сумме вычетов.
Теорема 2.Если функция  аналитична в расширенной плоскости (т.е. включающей точку
аналитична в расширенной плоскости (т.е. включающей точку 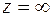 ), за исключением конечного числа изолированных особых точек
), за исключением конечного числа изолированных особых точек 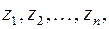 то
то
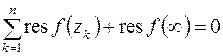 (8.9)
(8.9)
или
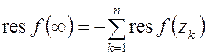 . (8.10)
. (8.10)
УПРАЖНЕНИЯ
101. Найти вычеты функции относительно их особых точек
а) 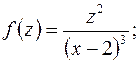 б)
б) 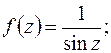
в) 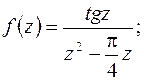 г)
г) 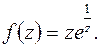
Решение. Особые точки данных функций и их характер определены в примере 97. Итак,
а) 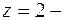 полюс 3-го порядка, поэтому по формуле (8.5) находим
полюс 3-го порядка, поэтому по формуле (8.5) находим
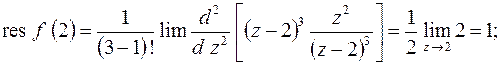
б) 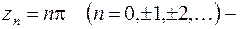 простые полюсы, поэтому, воспользовавшись формулой (8.4), получаем
простые полюсы, поэтому, воспользовавшись формулой (8.4), получаем
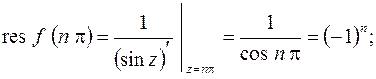
в) 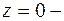 устранимая особая точка, следовательно,
устранимая особая точка, следовательно, 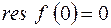 . Точка
. Точка 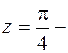 простой полюс, согласно (8.3) имеем
простой полюс, согласно (8.3) имеем
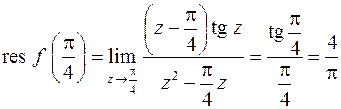 .
.
Точки 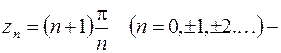 простые полюсы, тогда (8.4) получим
простые полюсы, тогда (8.4) получим
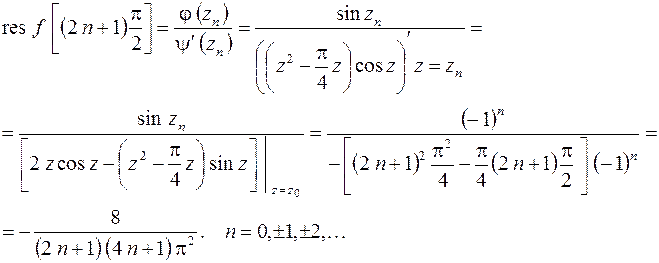
г) 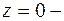 существенно особая точка. Для определения вычета относительно существенной точки надо получить разложение функции в окрестности этой точки. Как было показано в примере
существенно особая точка. Для определения вычета относительно существенной точки надо получить разложение функции в окрестности этой точки. Как было показано в примере
97г) 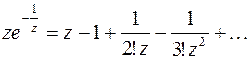 Согласно (8.2)
Согласно (8.2) 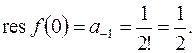
102.Вычислить вычеты относительно точки 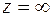 для функций:
для функций:
а) 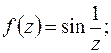 б)
б) 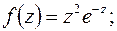
в) 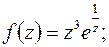 г)
г) 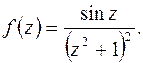
Решение. Вычет функции относительно бесконечной удаленной точки можно определять по формуле (8.7), для чего необходимо получить лорановское разложение в окрестности данной точки.
а) Так как 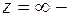 устранимая особая точка
устранимая особая точка 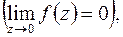 то лорановское разложение не содержит положительных степеней (главную часть), но содержит правильную часть, поэтому найдем ряд Лорана для данной функции в окрестности
то лорановское разложение не содержит положительных степеней (главную часть), но содержит правильную часть, поэтому найдем ряд Лорана для данной функции в окрестности 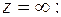
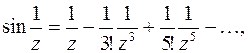 откуда видно, что
откуда видно, что 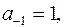 следовательно,
следовательно, 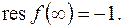
Из примера следует, что вычет функции относительно бесконечно удаленной устранимой особой точки может оказаться отличным от нуля.
б) Как показано в примере 98 в), ряд Лорана в окрестности 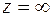 для данной функции имеет вид
для данной функции имеет вид 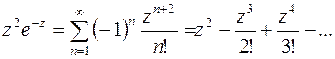 .Так как в разложении слагаемое
.Так как в разложении слагаемое 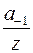 отсутствует, то
отсутствует, то 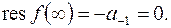
в) Как показано в примере 98 г), 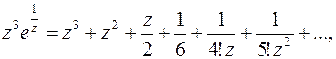 откуда следует, что
откуда следует, что 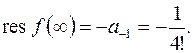
г) Разложить функцию в ряд Лорана с тем, чтобы вычислить вычет по формуле (8.7) трудно. Для вычисления вычета относительно бесконечно удаленной точки удобнее воспользоваться формулой (8.10). В этом случае нужно просто найти вычеты функции относительно её конечных изолированных особых точек 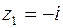 и
и 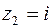 . Итак, по формуле (8.10) имеем
. Итак, по формуле (8.10) имеем 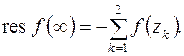 Указанные точки являются полюсами 2-го порядка. Тогда в силу (8.5) находим
Указанные точки являются полюсами 2-го порядка. Тогда в силу (8.5) находим 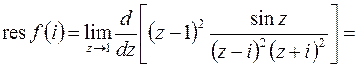
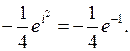
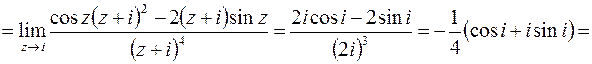
Аналогично находим 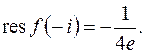
Таким образом, 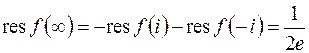 .
. 
103. Используя теоремы о вычетах, вычислить контурные интегралы:
а) 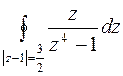 ; б)
; б) 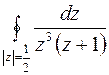 ; в)
; в) 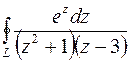 , где
, где 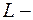 квадрат, ограниченный прямыми
квадрат, ограниченный прямыми 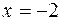 ,
,
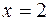 ,
, 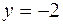 ,
, 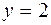 ;
;
г) 
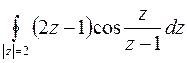 ; д)
; д) 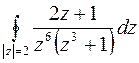 .
.
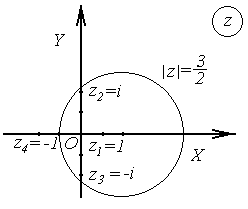 Рис.8.1 Рис.8.1 | Решение. а) Подынтегральная функция  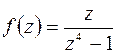 имеет четыре простых полюса, из которых три : имеет четыре простых полюса, из которых три :  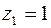 , ,  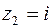 , , 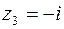 лежат в круге лежат в круге 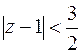  (рис.8.1). По основной теореме о вычетах (8.8) имеем (рис.8.1). По основной теореме о вычетах (8.8) имеем |
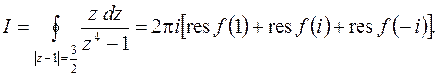 Вычеты вычисляем по формуле (8.4)
Вычеты вычисляем по формуле (8.4) 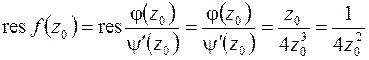 , значит,
, значит, 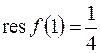 ,
, 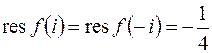 . Следовательно,
. Следовательно, 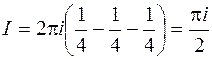 .
.
б) Подынтегральная функция 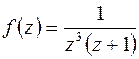 имеет две особые точки, из которых
имеет две особые точки, из которых 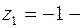 простой полюс,
простой полюс, 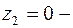 полюс 3-го порядка; причем
полюс 3-го порядка; причем 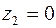 находится в круге
находится в круге 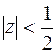 . Поэтому
. Поэтому 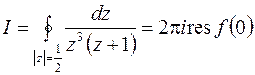 . По формуле (8.5)
. По формуле (8.5) 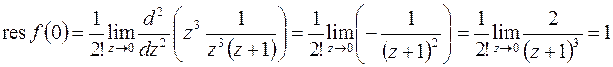 . Таким образом,
. Таким образом, 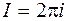 .
.
в) Подынтегральная функция 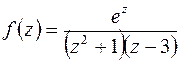 имеет три особых
имеет три особых
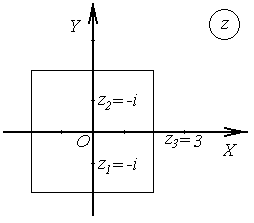 Рис.8.2 Рис.8.2 | точки 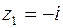 , , 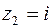 , , 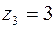 . Но . Но 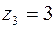 лежит вне квадрата (рис.8.2). Вычеты функции относительно ее простых полюсов лежит вне квадрата (рис.8.2). Вычеты функции относительно ее простых полюсов 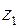 и и 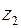 определяем по формуле (8.4), положив определяем по формуле (8.4), положив 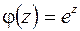 , , 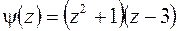 . Тогда в силу (8.8) получаем . Тогда в силу (8.8) получаем |
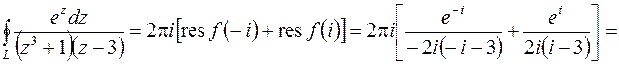
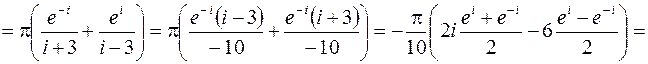
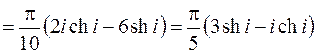 .
.
г) Функция 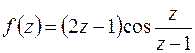 аналитична в круге
аналитична в круге 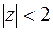 всюду, кроме точки
всюду, кроме точки 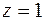 . Для определения типа особенности и вычета необходимо разложить функцию в ряд Лорана в кольце
. Для определения типа особенности и вычета необходимо разложить функцию в ряд Лорана в кольце 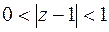 . Предварительно найдем
. Предварительно найдем
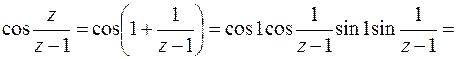
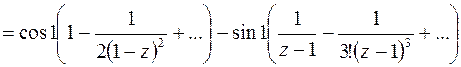 .
.
Легко видеть, что разложение функции 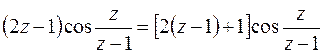 содержит бесконечно много членов с отрицательными степенями; значит
содержит бесконечно много членов с отрицательными степенями; значит 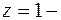 существенно особая точка. Так как вычет равен коэффициенту при
существенно особая точка. Так как вычет равен коэффициенту при 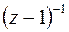 , то получаем
, то получаем 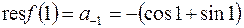 . Следовательно,
. Следовательно,
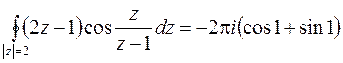 .
.
д) Подынтегральная функция имеет 3 особых точки: 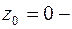 полюс 6-го порядка,
полюс 6-го порядка, 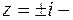 простые полюсы, и все они принадлежат кругу
простые полюсы, и все они принадлежат кругу 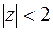 . Можно применить основную теорему о вычетах, но удобнее вычислять, пользуясь вычетом относительно бесконечно удаленной точки:
. Можно применить основную теорему о вычетах, но удобнее вычислять, пользуясь вычетом относительно бесконечно удаленной точки:
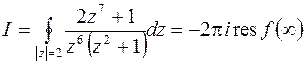 .
.
Разложение подынтегральной функции в ряд Лорана в окрестности точки 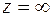 можно получить, деля числитель на знаменатель по правилу деления многочленов
можно получить, деля числитель на знаменатель по правилу деления многочленов 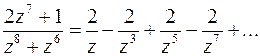 . Здесь
. Здесь 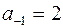 , значит,
, значит, 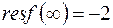 , следовательно,
, следовательно, 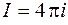 .
.
