Приведение нецентральной линии к каноническому виду

Сейчас мы освоим универсальный метод решения, который приближен к соответствующему теоретическому материалу стандартного курса аналитической геометрии. Таким образом, разобранные ниже задачи помогут сориентироваться не только в практике, но и лучше понять теорию.

Классический алгоритм приведения уравнения 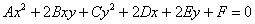к каноническому виду вкратце состоит в следующем:

На первом шаге выясняется угол поворота исходной линии относительно своего канонического положения и осуществляется поворот исходной системы координат 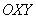на данный угол. В результате в новой прямоугольной системе координат 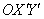уравнение исследуемой линии записывается в виде:

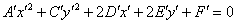
На втором шаге выделяются полные квадраты (при необходимости), и проводится параллельный перенос системы координат 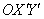началом в нужную точку 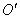. После чего в итоговой прямоугольной системе координат 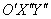получается уравнение 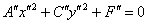, от которого до канонической формы рукой подать.

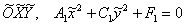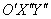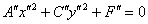Должен отметить неудачные обозначения со штрихами, но так принято практически во всех учебниках, и сейчас я буду придерживаться стандарта (ну, или почти придерживаться), поскольку немалой части аудитории нужно сдавать теорию. Штрихи, как вы поняли, кпроизводным функциям никакого отношения не имеют. В предыдущем параграфе я намеренно использовал обозначения вместо и чтобы не привить «чайникам» отвращение к теме.

Таким образом, универсальный способ приведения к линии 2-го порядка к каноническому виду предполагает два последовательных преобразования прямоугольной системы координат – поворот и параллельный перенос:

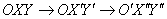
Как, наверное, все уже догадались и горестно вздохнули, удобный метод инвариантов позволял получить то же самое одним махом:

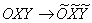
Но в параболическом случае мы вынуждены выехать с тихой просёлочной дороги метода инвариантов на оживлённую автостраду общего способа решения:

Пример 3

Привести уравнение линии второго порядка к каноническому виду

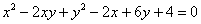
Выполнить чертёж.

Решение: в первую очередь выясним тип линии. Вычислим определитель, составленный из коэффициентов :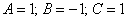

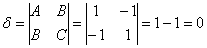, значит, у нас нецентральная линия и это может быть или парабола, или пара параллельных прямых (действительных либо мнимых), или пара совпавших прямых.

1) Осуществим поворот исходной системы координат 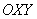и переход к новой системе координат 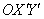ТАК, чтобы получить уравнение вида 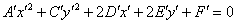(без слагаемого, «отвечающего» за поворот).

Искомый угол поворота найдём по формуле:
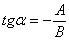или

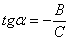
Внимание! Данная формула справедлива только для параболического случая ( ).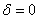

В нашем примере: .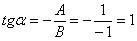

Вообще говоря, очевиден корень 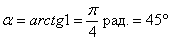, но здесь есть одна тонкость. Наверняка многие обратили внимание на тот факт, что если линию 2-го порядка (например, гиперболу) повернуть на 180 градусов, то она совпадёт сама с собой. Исключение составляет капризная парабола, ветви которой развернутся в противоположную сторону. А парабола у нас вполне может нарисоваться, поэтому, необходимо взять на заметку ещё один угол: 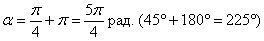, или, что то же самое: .

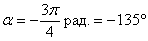Продолжаем:

Если осуществляется поворот прямоугольной системы координат 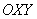на произвольный угол «альфа» и переход к новой системе координат 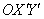, то формулы перехода от старых координат к новым координатам аналитически выражается следующей системой:

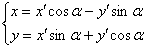, где «альфа» – угол данного поворота.

Из тригонометрических формул 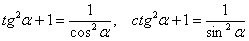нетрудно выразить синус и косинус через известный нам тангенс, однако выражения получаются не однозначными:

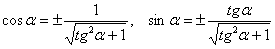
И сложившейся ситуации вполне прагматичным решением будет привлечь на помощь метод научного тыка. Не теряя времени, начинаем работать непосредственно с углом «альфа» и используем формулы 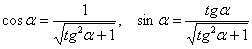. В результате дальнейших действий может получиться неканоническое уравнение (а это возможно в единственном случае – когда исследуемое уравнение задаёт параболу и та оказывается развёрнутой в другую сторону). Тогда следует рассмотреть противоположный угол поворота 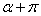системы координат, при этом значение тангенса угла останется тем же самым: 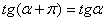, но формулы сменят знаки:
.

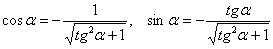Итак, для угла 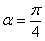выбираем первый комплект формул:

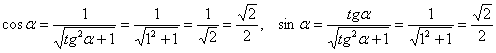
Подставим найденные (к слову, табличные) значения 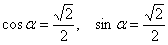в аналитические выражения поворота :

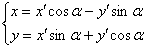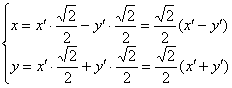
Теперь подставим 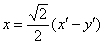и 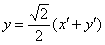в исходное уравнение :

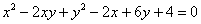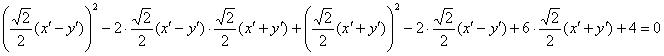
Нет причин в ужасе закрывать глаза ладонями – это ещё далеко не самое страшное, что может встретиться. Аккуратно-внимательно используем формулы сокращённого умножения, раскрываем скобки, приводим подобные слагаемые. И НЕ ТЕРЯЕМ ШТРИХИ:

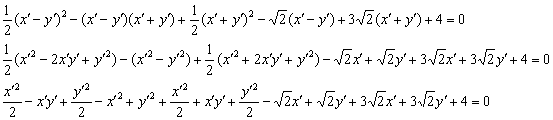
Очень многое сокращается, и в первую очередь, конечно же, «убирается» поворот (слагаемое, содержащее произведение ):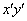

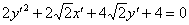
По всем признакам получается как раз парабола. Сократим каждое слагаемое на 2 и перебросим некоторые из них в правую часть:

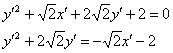
Перед слагаемым, содержащим «икс штрих», нарисовался знак минус, и это плохо. Для лучшего понимания я проиллюстрирую выполненные действия готовым чертежом:

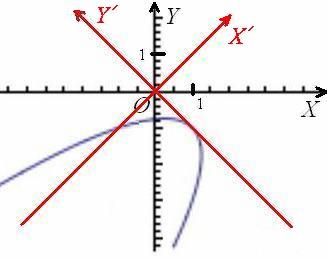
В результате поворота исходной системы координат 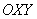вокруг точки 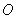на 45 градусов, мы перешли от уравнения 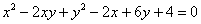к уравнению 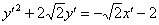в новой системе координат 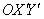. Но загвоздка состоит в том, что ветви параболы направлены «в противоход» оси 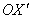(наклоните головы влево на 45 градусов), о чём нам и сообщил знак «минус» при переменной 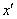нового уравнения.

Таким образом, выясняется, что поворот исходной системы координат 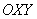следовало осуществить на угол 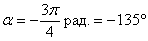. Ну что делать, не повезло, парабола запросто могла ведь «смотреть и в нужную сторону»….

Начинаем всё сначала. Тангенс правильного «кандидата» 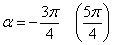тоже равен единице, и мы подставляем значение 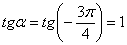в резервный комплект формул:

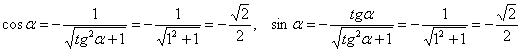
Подставим значения 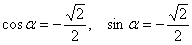в уравнения поворота:

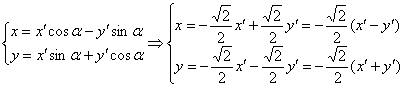
И, наконец, подставим 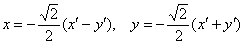в исходное уравнение :

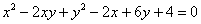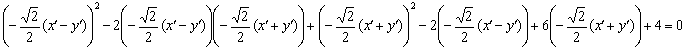
В качестве некоторой компенсации за наши мучения, для уравнения нецентральной линиисуществует эксклюзивная фишка, которую можно использовать как в целях самопроверки, так и по причине банальной лени. В результате рассматриваемой подстановки сумма 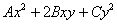упрощается до 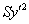, где 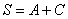– старый знакомый инвариант. Таким образом, громоздкая сумма первых трёх слагаемых 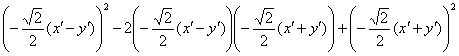превратится в :

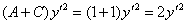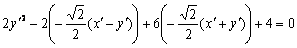
Но при оформлении, конечно, желательно всё расписать подробно, как мы это сделали в ходе предыдущей неудачной попытки.

Доводим уравнение до кондиции:

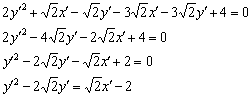
Ну вот, так бы сразу:

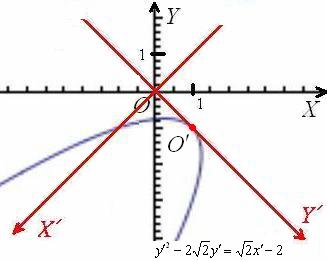
Проведём очередную разминку и заодно спасём от онемения пятую точку. Пожалуйста, встаньте лицом к монитору и наклонитесь вправо на 90 градусов. Теперь поверните голову ещё на 45 градусов в том же направлении и полюбуйтесь почти канонической параболой.

2) Осталось откалибровать уравнение 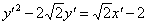до канонического вида параллельным переносом системы координат. Это значительно проще. Выделяем полный квадрат:

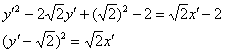
Таким образом, вершина параболы расположена в точке 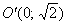– ВНИМАНИЕ, это координаты точки 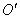в новойсистеме координат 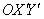. В позе страуса с наклоном головы вправо на 135 градусов можно отчётливо разглядеть, что у вершины параболы именно такие координаты!

Путём параллельного переноса системы координат 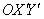началом в точку 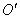перейдём к новой системе координат 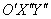. Аналитически данное действие выражается заменами 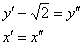, в результате которых получается долгожданное каноническое уравнение:

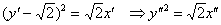
Выполним окончательный чертёж. Оси совпали, но это воля случая:

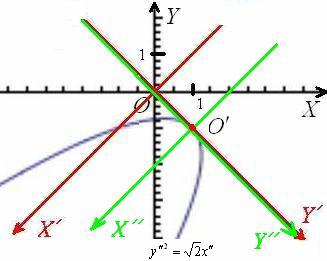
Страусы одобряют =)

Ответ: данная линия представляет собой параболу, каноническое уравнение 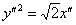которой получается путём поворота системы координат 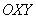вокруг своего начала на 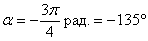и её дальнейшим параллельным переносом в точку .

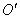Интересно отметить, что для параболы метод инвариантов, хоть и не работает, но тоже позволяет найти её каноническое уравнение. Во-первых, полезно запомнить характеристический признак: уравнение линии 2-го порядка, инварианты которого удовлетворяют условиям 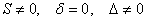, задаёт параболу и только её.

Представьте, что вы видите уравнение 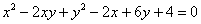в первый раз. Да… с оттенком черного юмора получилась фраза =) Выпишем коэффициенты 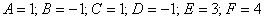и вычислим инварианты:

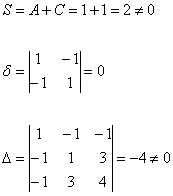
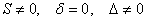, следовательно, данное уравнение определяет именно параболу, а не какую-то другую линию.

И, во-вторых, найденные инварианты позволяют найти фокальный параметр 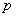параболы 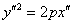по формуле:

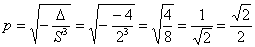
Таким образом:

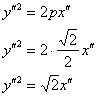
Желающие могут использовать данный путь для самопроверки или даже в качестве основного решения в критической ситуации – когда не получается найти уравнение параболы стандартным способом, но жизненно важно родить хоть что-то. Кроме того, нетрудно найти угол поворота, а там, глядишь, и прокатит.

Следующий пример для самостоятельной разработки:

Пример 4

Привести уравнение линии второго порядка к каноническому виду

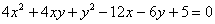
Выполнить чертёж, на котором отразить все преобразования системы координат.

Краткий алгоритм решения с повторением важных моментов чуть ниже, а примерный образец оформления задачи – в конце урока.

Следует отметить, что на практике достаточно популярна урезанная версия задачи. Случай, когда нужно выполнять только параллельный перенос, досконально изучен на предыдущих уроках, но бывает и так, что необходимо осуществить только поворот системы координат.

Так, например, в уравнении 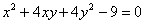отсутствуют слагаемые, «отвечающие» за параллельный перенос. Угол поворота системы координат находится элементарно: 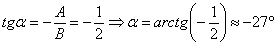, и, более того, с помощью «ускорителя» 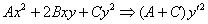легко узнать итоговое уравнение:

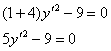
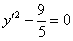– две параллельные прямые. Ещё раз подчёркиваю, что полученное уравнение имеет место в новой системе координат 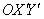, повёрнутой относительно исходной системы 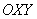на угол 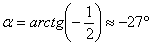, и, соответственно, прямые 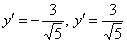будут параллельны новой оси .

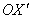Полезно знать, что вырожденное уравнение параболического типа несложно выразить в явном виде и в исходной системе координат – проходят тривиальные алгебраические преобразования. Например:

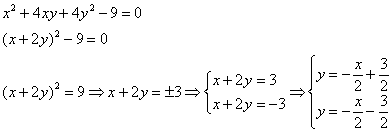
Полученный результат удобно использовать для самопроверки и выполнения чертежа.

Что касается инвариантов, то дела обстоят хуже. Если для параболы мы ещё смогли вытянуть некоторую информацию из инвариантов, то здесь будем созерцать малополезный набор .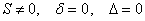

Систематизируем порядок действий в параболическом случае:

1) Из формулы 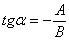или 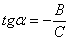находим угол поворота исходной системы координат :

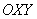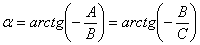
2) Для данного угла «альфа» рассчитываем 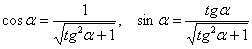. При этом проводим максимальные упрощения: выносим из-под корней всё, что можно вынести, и избавляемся от многоэтажных дробей, если таковые образовались.

3) Подставляем найденные значения 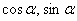в формулы поворота .

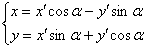4) Подставляем найденные выражения поворота 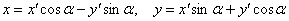в исходное уравнение 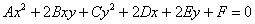, внимательно раскрываем все скобки и приводим подобные слагаемые, в результате чего в новой системе координат 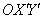должно получиться уравнение вида 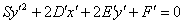, где .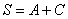

4*) Примерно в 15%-ах случаев (с нецентральной линией) может получиться уравнение, которое определяет параболу, развёрнутую относительно своего канонического положения (положительного направления оси 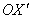) на 180 градусов. Тогда следует вернуться к Пункту №2 алгоритма, рассмотреть противоположный угол поворота 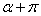и использовать формулы 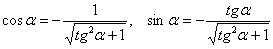, не забывая, что само значение тангенса осталось таким же: .

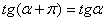5) В полученном уравнении 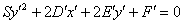выделяем полный квадрат (если необходимо), в результате чего должно получиться уравнение вида 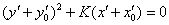, где 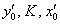– некоторые константы. И, наконец, после параллельного переноса системы координат 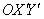началом в точку 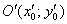(замен 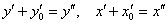и перехода к окончательной системе координат 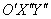) наша цель достигнута: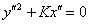

6) Чертёж. Повторюсь, что во многих случаях пойдёт и схематическая версия, поскольку рисовать линии 2-го порядка под градусом – занятие нелёгкое.

Рассмотренная схема решения с некоторыми изменениями применима и к эллиптическому, и к гиперболическому случаю:

– В пункте №1 угол поворота находим по формуле 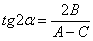. Если 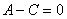, то .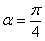

– Центральные линии «не страдают синдромом параболы», поэтому формулы 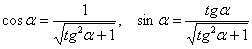безотказно срабатывают с первой попытки, и дополнительный пункт №4* вообще отпадает. Но зато возрастает техническая сложность подстановок 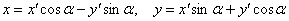пункта №4 и дальнейшие преобразования. А сложность возрастает по той причине, что уравнение центральной линии содержит оба квадрата и в результате подстановки должно получиться полное уравнение вида 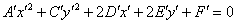. Аппетитный пирожок 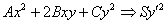параболического случая, разумеется, покрывается плесенью.

Любители потягать брёвна могут прорешать вторым способом Примеры №№1,2.

Таким образом, рассмотренный метод решения универсален и применим к любой линии 2-го порядка. Более того, он недалеко ушёл от соответствующего теоретического материала, и теперь вам будет значительно легче разобраться в теории. На первом курсе Физмата мне «повезло» с билетом по аналитической геометрии и я где-то 3 часа мучался с поворотом линии 2-го порядка, решая задачу в общем виде. Поэтому сейчас было бы просто кощунственно скрыть от вас эти знания =)

Пример 2:Решение: приведём данной линии к каноническому виду 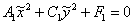в новой системе координат .

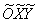Из уравнения 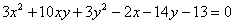находим коэффициенты:

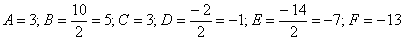
Вычислим инварианты:

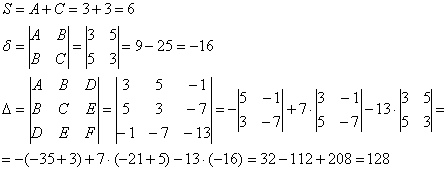
Примечание: последний определитель выгоднее раскрыть по 3-ей строке либо 3-му столбцу.

Составим и решим систему:

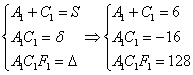
Из 1-го уравнения выражаем 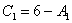– подставляем во второе уравнение:

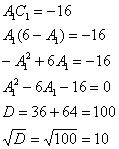
Таким образом, получаются две пары корней:

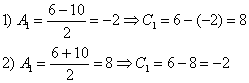
Примечание: решение несложно найти и подбором.

Подставим 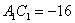в третье уравнение системы:

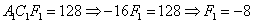
Подставляем (сначала мысленно либо на черновике!) значения 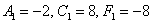в уравнение :

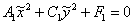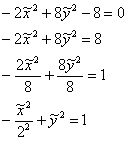
В результате получена неканоническая запись гиперболы (см. материалы параграфао повороте гиперболы), т.е. первый набор корней нас не устраивает.

Подставляем второй комплект корней :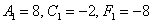

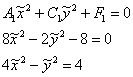
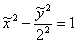– гипербола с центром в точке 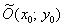, действительной полуосью 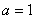, мнимой полуосью .
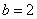Примечание: опытный читатель сразу выберет 2-ой комплект корней, так как увидит, что получается гипербола, а у её канонического уравнения коэффициент при 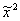должен быть положительным: .

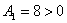Координаты 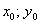начала новой системы координат 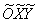найдём из решения системы:

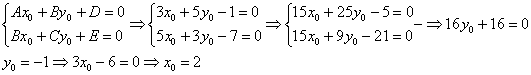
Таким образом: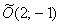
Найдём угол поворота новой системы координат 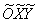относительно старой:

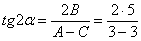
Так как 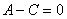, то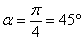

Выполним чертёж:

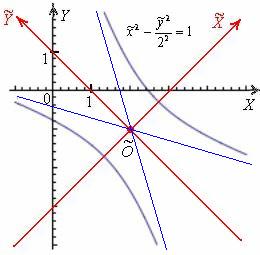
Ответ: 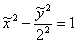– каноническая гипербола с полуосями 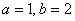в системе координат 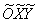с началом в точке 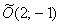(координаты старой системы), повёрнутой относительно исходной системы координат на угол .

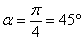Дополнительная информация: гиперболический случай выражается аналитическим условием 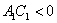( 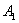и 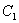имеют разные знаки). Если инвариант 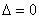, то коэффициент 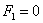, и гипербола вырождается в две пересекающиеся прямые (пункт №5 классификации). В нашем примере гипотетически получилось бы уравнение: 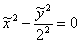– двух пересекающихся прямых 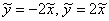, которые, кстати, представляют собой асимптоты рассмотренной гиперболы (изображены синим цветом на чертеже).

Пример 4:Решение: сначала выяснить тип линии. Для этого вычислим определитель, составленный из коэффициентов :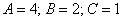
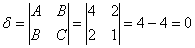, значит, данное уравнение задаёт нецентральную линию.

Осуществим поворот прямоугольной системы координат 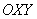и переход к новой системе координат 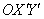так, чтобы получить уравнение вида 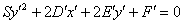, где .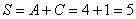

Найдём искомый угол поворота:

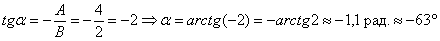
Если 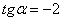, то:

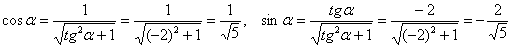
Подставим 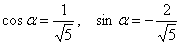в формулы поворота:

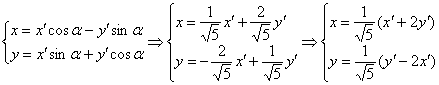
Подставим 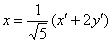и 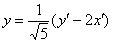в исходное уравнение :

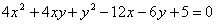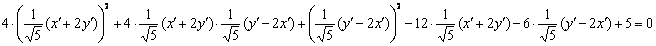
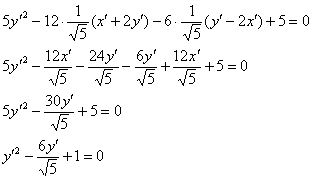
Выделим полный квадрат:

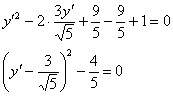
Осуществим параллельный перенос системы координат 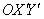началом в точку 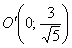. Проведём замену 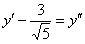и запишем уравнение линии в новой системе координат :

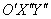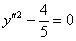– пара прямых 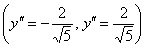, параллельных оси .
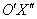Выполним чертёж:

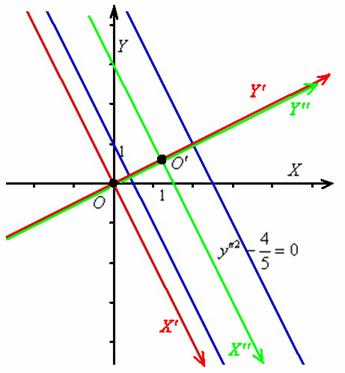
Ответ: данная линия представляет собой пару параллельных прямых, каноническое уравнение 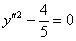которых получается путём поворота системы координат 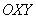вокруг своего начала на угол 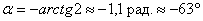и её дальнейшим параллельным переносом в точку .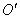