Приведение квадратичной формы к каноническому виду

ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 2

1. Применение элементарных преобразований для нахождения обратных матриц и для решения матричных уравнений.

http://www.mathprofi.ru/metod_zhordano_gaussa_nahozhdenie_obratnoi_matricy.html

http://www.cleverstudents.ru/matrix/finding_the_inverse_matrix.html

Предположим, дана система с тремя уравнениями, тремя неизвестными и записана её расширенная матрица 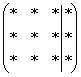. В наиболее распространенном случае получаются стандартные ступеньки 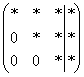, и так каждый день…. Одно и то же – как беспросветный ноябрьский дождь.

На некоторое время развевает тоску другой способ приведения матрицы к ступенчатому виду: 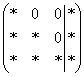, причём он совершенно равноценен и может быть неудобен только по причине субъективного восприятия. Но всё рано или поздно приедается…. И подумал тогда Жордан – а зачем вообще мучиться с обратным ходом гауссовского алгоритма? Не проще ли сразу получить ответ 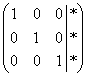с помощью дополнительных элементарных преобразований?

Пример 1

Решить систему методом Гаусса-Жордана

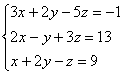
Решение: это первое задание урока Метод Гаусса для чайников, где мы 5 раз трансформировали расширенную матрицу системы и привели её к ступенчатому виду:

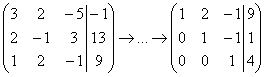
Теперь вместо обратного хода в игру вступают дополнительные элементарные преобразования. Сначала нам необходимо получить нули на этих местах: ,
а потом ещё один ноль вот здесь: .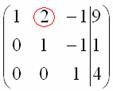

Идеальный с точки зрения простоты случай:

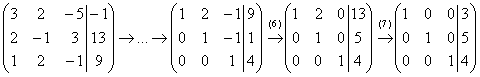
(6) Ко второй строке прибавили третью строку. К первой строке прибавили третью строку.

(7) К первой строке прибавили вторую строку, умноженную на –2.

Не могу удержаться от иллюстрации итоговой системы:

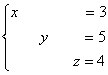
Ответ: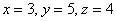

Пример 2

Решить систему линейных уравнений методом Гаусса-Жордана.

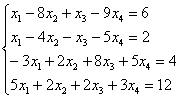
Решение: первая часть задания хорошо знакома:

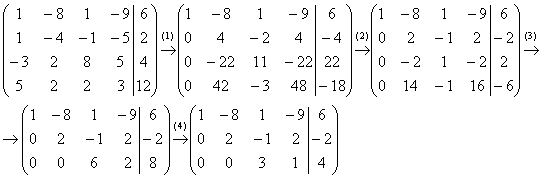
(1) Ко второй строке прибавили первую строку, умноженную на –1. К третьей строке прибавили первую строку, умноженную на 3. К четвертой строке прибавили первую строку, умноженную на –5.

(2) Вторую строку разделили на 2, третью строку разделили на 11, четвёртую строку разделили на 3.

(3) Вторая и третья строки пропорциональны, 3-ю строку удалили. К четвёртой строке прибавили вторую строку, умноженную на –7

(4) Третью строку разделили на 2.

Очевидно, что система имеет бесконечно много решений, и наша задача – привести её расширенную матрицу к виду .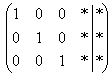

Как действовать дальше? Прежде всего, следует отметить, что мы лишились вкусного элементарного преобразования – перестановки строк. Точнее говоря, перестаить-то их можно, но в этом нет смысла (просто выполним лишние действия). И далее целесообразно придерживаться следующего шаблона:

Находим наименьшее общее кратное чисел третьего столбца (1, –1 и 3), т.е. – наименьшее число, которое бы делилось без остатка и на 1, и на –1 и на 3. В данном случае, это, конечно же, «тройка». Теперь в третьем столбце нам нужно получить одинаковыепо модулючисла, и этими соображениями обусловлено 5-е преобразование матрицы:

(5) Первую строку умножаем на –3, вторую строку умножаем на 3. Вообще говоря, первую строку можно было умножить тоже на 3, но это было бы менее удобно для следующего действия. К хорошему привыкаешь быстро:

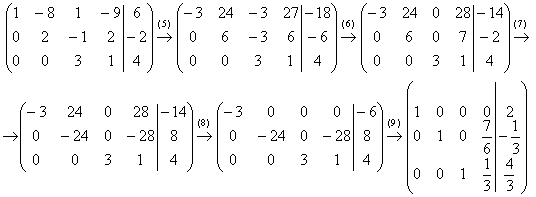
(6) Ко второй строке прибавили третью строку. К первой строке прибавили третью строку.

(7) Во втором столбце два ненулевых значения (24 и 6) и нам снова нужно получить одинаковые по модулю числа. В данном случае всё сложилось довольно удачно – наименьшее кратное 24, и эффективнее всего умножить вторую строку на –4.

(8) К первой строке прибавили вторую.

(9) Заключительный штрих: первую строку разделили на –3, вторую строку разделили на –24 и третью строку разделили на 3. Это действие выполняется В ПОСЛЕДНЮЮ ОЧЕРЕДЬ! Никаких преждевременных дробей!

В результате элементарных преобразований получена эквивалентная исходной система:

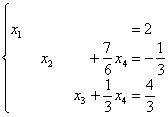
Элементарно выражаем базисные переменные через свободную:

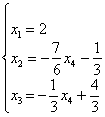
и записываем:

Ответ: общее решение: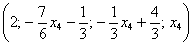

Пример 3

Найти базисное решение с помощью элементарных преобразований

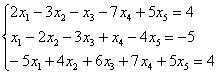
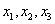Такая формулировка задачи предполагает использование метода Гаусса-Жордана, и в образце решения матрица приводится к стандартному виду с базисными переменными . Однако всегда держите на заметке, что в качестве базисных можно выбрать и другие переменные. Так, например, если в первом столбце громоздкие числа, то вполне допустимо привести матрицу к виду (базисные переменные 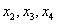), или к виду (базисные переменные 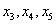), или даже к виду с базисными переменными 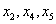. Существуют и другие варианты.

Но всё-таки это крайние случаи – не стОит лишний раз шокировать преподавателей своими знаниями, техникой решения и уж тем более не надо выдавать экзотических жордановсих результатов вроде 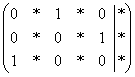. Впрочем, бывает трудно удержаться от нетипового базиса, когда в исходной матрице, скажем, в 4-м столбце есть два готовых нуля.

2. Неравенство Коши-Буняковского для векторов евклидова пространства.

http://www.studfiles.ru/preview/5058982/page:2/

Теорема 3.1.Для любых векторов х, уевклидова пространства 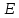справедливо неравенство Коши - Буняковского

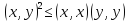(3.1)

При 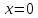обе части неравенства (3.1) равны нулю согласно свойству 3.3, значит, неравенство выполняется. Отбрасывая этот очевидный случай, будем считать, что 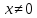.Для любого действительного числа 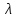, в силу аксиомы г), выполняется неравенство

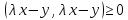(3.2)

Преобразуем левую часть неравенства, используя аксиомы и свойства скалярного умножения:

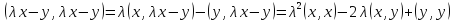
Мы получили квадратный трехчлен относительно параметра 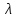(коэффициент 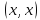при 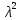согласно аксиоме г) ненулевой, так как 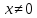,неотрицательный при всех действительных значениях параметра. Следовательно, его дискриминант равен нулю или отрицательный, т.е.

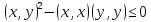
Что и требовалось доказать.

Доказательство неравенства Коши — Буняковского выглядит достаточно просто. Тем не менее это неравенство очень полезное. Применяя его в конкретных евклидовых пространствах, мы получаем некоторые хорошо известные в анализе и алгебре неравенства.

Пример 3.5.В случае линейного арифметического пространства 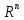неравенство Коши — Буняковского трансформируется в неравенство Коши:

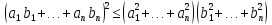
В евклидовом пространстве 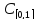, скалярное произведение в котором выражается определенным интегралом (см. пример 3.4), неравенство Коши — Буняковского превращается в неравенство Буняковского (называемое также неравенством Шварца):

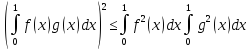
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 3

1. Правило Крамера для решения систем линейных уравнений.

http://function-x.ru/systems_kramer.html

Метод Крамера основан на использовании определителей в решении систем линейных уравнений. Это значительно ускоряет процесс решения.

Метод Крамера может быть использован в решении системы стольких линейных уравнений, сколько в каждом уравнении неизвестных. Если определитель системы не равен нулю, то метод Крамера может быть использован в решении, если же равен нулю, то не может. Кроме того, метод Крамера может быть использован в решении систем линейных уравнений, имеющих единственное решение.

Определение. Определитель, составленный из коэффициентов при неизвестных, называется определителем системы и обозначается (дельта).

Определители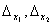

получаются путём замены коэффициентов при соответствующих неизвестных свободными членами:

;

.

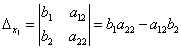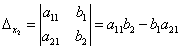Формулы Крамера для нахождения неизвестных:

.

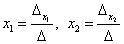Найти значения 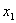и 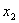возможно только при условии, если

.

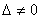Этот вывод следует из следующей теоремы.

Теорема Крамера. Если определитель системы отличен от нуля, то система линейных уравнений имеет одно единственное решение, причём неизвестное равно отношению определителей. В знаменателе – определитель системы, а в числителе – определитель, полученный из определителя системы путём замены коэффициентов при этом неизвестном свободными членами. Эта теорема имеет место для системы линейных уравнений любого порядка.

Пример 1. Решить систему линейных уравнений:

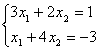. (2)

Согласно теореме Крамера имеем:

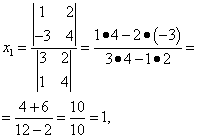
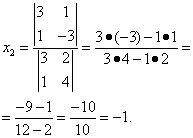
Итак, решение системы (2):

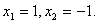
2 Неравенство треугольника для векторов евклидова пространства.

http://www.studfiles.ru/preview/6139559/page:3/

Неравенство треугольника.

Из неравенства Коши-Буняковского следует еще одно важное неравенство, называемое неравенством треугольника,

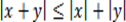
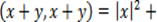
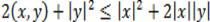
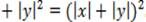
Знак равенства имеет место, если 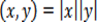, т.е. если угол междуx и y равен нулю, и только в этом случае. Неравенство треугольника для векторов – направленных отрезков – означает, что длина стороны треугольника меньше суммы длин остальных сторон.

ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 4

1. Ранг матрицы. Линейная зависимость векторов.

http://studopedia.ru/3_61845_rang-matritsi.html

Рангом матрицы А размера 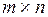называется максимальное число линейно независимых векторов в системе 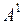, ,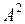…, 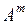ее строк.

Другими словами, рангом матрицы называется такое число 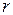, что:

1) среди строк матрицы имеются 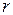линейно независимых;

2) любые ( 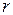+1) строки линейно зависимы.

Максимальное число линейно независимых строк матрицы образуют базис и называются базисными.

Ранг матрицы А обозначают символом r(А).

Теорема 3.1. Ранг совокупности строк матрицы равен рангу совокупности столбцов матрицы.

Из теоремы 3.1 следует, что если матрица А имеет размер ,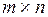
то ранг матрицы не превосходит наименьшего из значени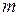й и :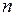

r(А) £ min( , ).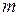

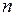Теорема 3.1 утверждает равноправность строк и столбцов матрицы и позволяет нам все последующие свойства ранга матрицы устанавливать лишь для строк и быть уверенными в справедливости их и для столбцов.

Из определения ранга матрицы можно сделать следующие выводы.

1. Если ранг матрицы А равен r, то существует r линейно независимых (базисных) строк матрицы, а остальные (m – r) строк линейно выражаются через указанные r строк.

□ Если r(A)=r, то по определению ранга матрицы среди строк матрицы А найдется r линейно независимых строк. Присоединив любую из остальных (m – r) строк к указанным r строкам, получим систему из 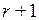строки, которые по определению ранга матрицы должны быть линейно зависимы. Значит, по свойству 6° линейной зависимости векторов (п.1.2) присоединенная строка линейно выражается через указанные r строк. ■

2. Если какие-то r строк матрицы А линейно независимы, а

остальные (m – r) строк линейно выражаются через указанные r строк, то ранг матрицы А равен r.

□ Пусть для определенности линейно независимы первые r строк матрицы А: 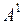, ,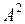…, 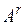– линейно независимы и любая другая строка матрицы линейно через них выражается. Тогда эти r строк образуют базис системы всех строк матрицы А. Рассмотрим любые 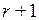строки матрицы А. Если бы они оказались линейно независимыми, то это означало бы, что в системе всех строк матрицы А можно найти базис, состоящий более чем из r векторов, а это невозможно. Значит, любые 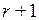строк матрицы А линейно зависимы и ранг матрицы А равен r. ■

Исходя из определения, найдем ранг матрицы в некоторых важных для дальнейшего изложения случаях.

1. Пусть А – нулевая матрица, т.е. А = 0. Тогда матрица А есть совокупность нулевых векторов и по свойству 2° линейной зависимости (п.1.2) такая совокупность линейно зависима, т.е. r(А) = 0.

2. Рассмотрим ступенчатую матрицу вида (3.4):

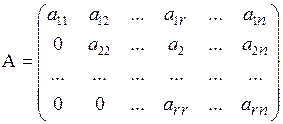, где .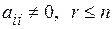

Строки 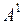, ,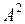…, 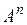матрицы А представляют диагональную систему векторов (1.6), а значит, эта система линейно независима и ранг матрицы А равен числу ее строк, т.е. r(А)=r.

3. Рассмотрим матрицу треугольного вида (3.3). Эта матрица есть частный случай матрицы вида (3.4) при 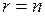, поэтому ранг матрицы треугольного вида равен числу ее строк, т.е. порядку этой матрицы.

4. Рассмотрим диагональную матрицу 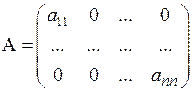, у которой все элементы главной диагонали ненулевые, т.е. 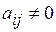при 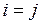. Эта матрица является частным случаем матрицы (3.4). Матрица имеет n линейно независимых строк, поэтому ранг такой матрицы равен ее порядку.

Пример. Найти ранг матрицы .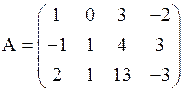

□ Матрица А содержит три вектор-строки: , , .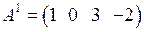

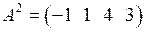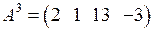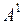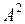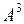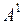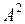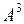Векторы и неколлинеарны, а значит линейно независимы. Вектор является линейной комбинацией векторов и : =3 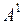+ 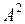, значит векторы 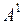, , 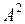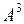линейно зависимы. Максимальное число линейно независимых векторов в системе 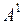, , 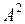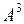строк матрицы А равно 2, следовательно, ранг матрицы А равен 2, r(А)=2. ■

2. Ортонормированный базис. Процесс ортогонализации базиса.

http://studopedia.ru/3_18408_ortonormirovannie-bazisi.html

Базис пространства 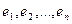называется ортогональным, если базисные векторы попарно ортогональны. Базис называется ортонормированным, если при этом базисные векторы имеют единичную длину.

Теорема.Любая ненулевые взаимно ортогональные векторы 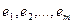линейно независимы. Если 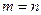, то эти векторы образуют ортогональный базис.

Доказательство. Пусть 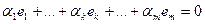, причем 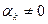. Тогда

,

,

,

.

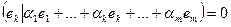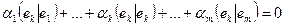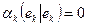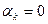Полученное противоречие доказывает теорему.

Теорема.В любом конечномерном пространстве существует ортонормированный базис.

Доказательство теоремы немедленно следует из того, что существует базис 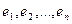, в котором квадратичная форма, соответствующая скалярному произведению, имеет канонический вид

,

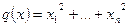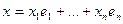( ). В этом базисе скалярное произведение векторов 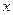и 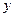задается формулой 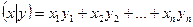. Но это и означает, что базис 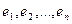ортонормированный.

16.6. Процесс ортогонализации Грама – Шмидта.Пусть 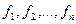- произвольный базис евклидова пространства. Мы будем строить новый – ортонормированный – базис пространства .

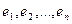В качестве первого вектора нового базиса возьмем вектор 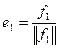. Таким образом, длина вектора 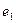равна 1. Прежде, чем построить второй вектор нового базиса, построим вектор :

.

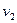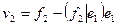Вектор 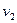не может быть нулевым, поскольку векторы 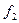и 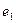линейно независимы. Заметим, что векторы 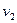и 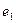ортогональны. В качестве второго базисного вектора возьмем вектор 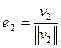. Теперь будем строить третий базисный вектор. Сначала возьмем вектор

.

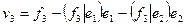Этот вектор – ненулевой, так как векторы 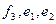линейно независимы,- ортогонален векторам 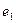и 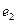. Остается только нормировать его: 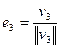. Алгоритм ясен: имея 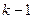вектор нового базиса, мы построим сначала вектор

.

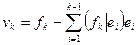Этот вектор ненулевой и ортогональный векторам 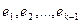. Нормировав его, получаем 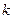-й вектор нового базиса .

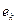16.7. Матрица Грама.Пусть 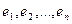- произвольный базис пространства. В этом базисе скалярное произведение, как и любая билинейная форма, имеет свою матрицу. Легко видеть, что это за матрица. Так как

,

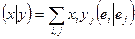то элементами этой матрицы являются скалярные произведения базисных векторов.

Определение.Матрицей Грама векторов 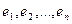называется матрица 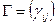, элементы которой являются скалярными произведениями этих векторов: 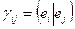. Можно записать в матричном виде .

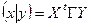Очевидно, что матрица 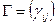является симметричной с определителем, большим нуля.

Матрицу Грама можно построить не только для базисных векторов. Возьмем произвольные векторы 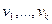и построим матрицу Грама аналогичным образом:

.

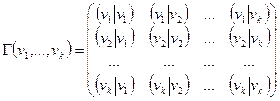Теорема.Определитель матрицы Грама произвольных векторов 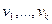положителен, если эти векторы линейно независимы, и равен нулю в противном случае.

Доказательство. Если векторы линейно независимы, построим подпространство 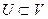, в котором эти векторы будут базисом. (это подпространство является множеством всевозможных линейных комбинаций векторов 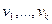). Скалярное произведение, ограниченное на это подпространство, по-прежнему остается симметричной положительно определенной билинейной формой. Матрица Грама этих векторов является матрицей этой формы, поэтому ее определитель больше нуля.

Если векторы линейно зависимы, то один из них линейно выражается через другие, например, 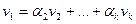. Подставим в матрицу 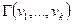вместо вектора 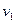это выражение. Учитывая линейность скалярного произведения, получим, что первый столбец является линейной комбинацией остальных столбцов. Отсюда следует, что определитель матрицы равен нулю.

Очевидно, что матрица Грама векторов ортонормированного базиса является единичной.

16.8. Переход от одного ортонормированного базиса к другому. Пусть 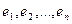- ортонормированный базис пространства, 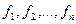- некоторый другой ортонормированный базис. Переход от старого базиса к новому осуществляется с помощью матрицы перехода 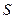. Поскольку в ортонормированном базисе матрица скалярного произведения является единичной, то 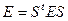, или 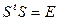. Получается, что матрица 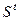является обратной л матрице : .

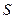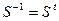Определение.Матрица 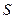, для которой выполняется условие 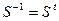, называется ортогональной.

Ортогональные матрицы и только они являются матрицами перехода от одного ортонормированного базиса к другому.

Условие ортогональности матрицы можно записать через ее элементы:

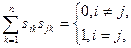
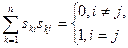
Очевидным свойством ортогональных матриц является равенство 1 их определителя.

ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 5

1. Теорема о базисном миноре.

https://ru.wikiversity.org/wiki/Ранг_матрицы._Теорема_о_базисном_миноре._Теорема_о_ранге_матрицы

http://studopedia.ru/7_153849_bilet--ponyatie-ranga-matritsi-teorema-o-bazisnom-minore.html

Теорема о базисном миноре.Столбцы матрицы А, входящие в базисный минор, образуют линейно независимую систему. Любой столбец матрицы А линейно выражается через базисные столбцы.

Доказательство.A_mxn = || a_ij ||_mxn Пусть k – порядок базисного минора. Без ограничения общности считаем, что базисный минор расположен в левом верхнем углу.

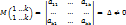
1) Если базисные столбцы линейно зависимы, то столбцы базисного минора так же линейно зависимы => хотя бы один из столбцов линейно выражается через остальные, т.е.. является их линейной комбинацией => Δ = 0, что противоречит условию => базисные столбцы линейно независимы.

2) Зафиксируем произвольный столбец матрицы А, например 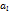_. Покажем, что 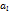линейно выражается через базисные столбы. Построим определитель

(1≤ l ≤n) (1≤ i ≤m)

Если i < k или l < k, то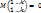

Рассмотрим случай i > k, l > k Тогда 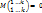как минор k+1– го порядка в матрице А. Обозначим А₁, …, А_k, A_k+1 алгебраические дополнения к последней строке 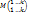Эти величины не зависят от элементов i-ой строки. Кроме того A_k+1 = Δ ≠ 0. Разложим минор по последней строке. a_i1 A₁+…+ a_ik A_k + a_il Δ = 0

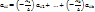l = 1, …, n ч.т.д.

Следствие 1. Пусть А_mxn Если Rg A < n, то столбцы матрицы линейно зависимы.

Доказательство.Пусть Rg A = k < n, значит в матрице существует базисный минор порядка k. Не ограничиваясь общности будем считать, что _↓a₁, …, _↓a_k базисные. Т.к.. k < n, то ∃ _↓a_k+1. По теореме о базисном миноре столбец _↓a_k+1 выражается через базисные, т.е.. _↓a₁, …, _↓a_k, _↓a_k+1 – линейно зависимы => матрица содержит линейно зависимую подсистему => матрица линейно зависима.

Следствие 2.Пусть А – квадратная матрица. det A = 0 óстолбцы матрицы линейно зависимы.

Доказательство.Если столбцы линейно зависимы, то det A = 0. Пусть det A = 0, тогда Rg A < n, т.е.. число столбцов больше ранга => (из следствия 1) столбцы матрицы линейно зависимы.

2 Билинейные формы и их свойства.

http://www.studfiles.ru/preview/1719982/page:40/

Определение 11.1. Билинейной формой называется функция (отображение) f: V ´ V ® R (или C), где V – произвольное векторное пространство, и для любых векторов x, y Î V и любого числа λÎR(или C) выполняются соотношения

f(x + y, z) = f(x, y) + f(z, y),

f(x, y + z) = f(x, y) + f(x, z),

f(λx, y) = λf(x, y),

f(x, λy) = λf(x, y).

Обозначим число, получаемое в результате отображения пары векторов x и y, как A(x, y) .

Определение 11.2. Билинейная форма A(x, y) называется симметрической, если для любых x, y Î V выполняется: A(x, y) = A(y, x).

Определение 11.3. Билинейная форма A(x, y) называется кососимметрической, если для любых x, y Î V выполняется: A(x, y) = –A(y, x).

Свойства билинейных форм

Любую билинейную форму можно представить в виде суммы симметричной кососимметричной форм.

При выбранном базисе e₁, e₂, …, e_n в векторном пространстве V любая билинейная форма A однозначно определяется матрицей

A(е) = ,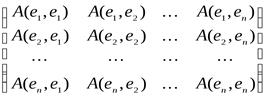

так, что для любых x = x₁e₁ + x₂e₂ + … + x_ne_n, y = y₁e₁ + y₂e₂ + … + y_ne_n;

A(x, y) = (x₁ x₂ … x_n)× 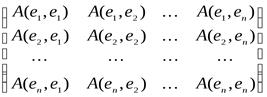× 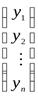, то есть

A(x, y) = 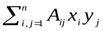,где А_ij = A(e_i, e_j). (1)

Вид (1) назовем общим видом билинейной формы в n-мерном векторном пространстве.

Замечание. Если билинейная форма A(x, y) симметрическая, то и матрица (A_ij) будет симметрической, то есть A_ij = A_ji для "i, j = 1, 2, …, n. Если билинейная форма A(x, y) кососимметрическая, то и матрица (A_ij) будет кососимметрической, то есть A_ij = –A_ji для "i, j = 1, 2, …, n.

Преобразование матрицы билинейной формы при переходе к новому базису. Ранг билинейной формы

Пусть в векторном пространстве V заданы два базиса e = {e₁, e₂, …, e_n} и f = {f₁, f₂, …, f_n}. Пусть A(e) = (а_ij) и A(f) = (b_ij) – матрицы билинейной формы A в указанных базисах.

Теорема 11.1.Матрицы A(e) и A(f) билинейной формы A(x, y) в базисах {e} и {f} связаны соотношением

A(f) = C^t×A(e)×C, (*),

где C – матрица перехода от базиса {e} к базису {f}, а C^t –транспонированная матрица C.

Следствие. Ранг матрицы A(f) равен рангу матрицы A(e).

Это утверждение следует из равенства (*): так как С – матрица перехода от одного базиса к другому, то матрица С и матрица C^t– невырожденные, поэтому умножение на них матрицы A(e) не меняет ее ранга.

Определение 11.4. Рангом билинейной формы, заданной в конечномерном векторном пространстве V , называется ранг матрицы этой формы в произвольном базисе пространства V.

Определение 11.5. Билинейная форма называется невырожденной, если ее ранг равен размерности пространства V и вырожденной, если ее ранг меньше размерности пространства V.

ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 6

1. Метод Гаусса решения систем линейных уравнений.

http://function-x.ru/systems_gauss.html

Метод Гаусса, называемый также методом последовательного исключения неизвестных, состоит в том, что при помощи элементарных преобразований систему линейных уравнений приводят к такому виду, чтобы её матрица из коэффициентов оказалась трапециевидной или близкой к трапециевидной. Пример такой системы - на рисунке сверху.

В ней, как видим, третье уравнение уже не содержит переменных 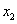и 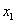, а второе уравнение - переменной .

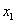После того, как матрица системы приняла трапециевидную форму, уже не представляет труда разобраться в вопросе о совместности системы, определить число решений и найти сами решения.

Преимущества метода Гаусса:

1. при решении систем линейных уравнений с числом уравнений и неизвестных более трёх метод Гаусса не такой громоздкий, как метод Крамера, поскольку при решении методом Гаусса необходимо меньше вычислений;
2. методом Гаусса можно решать неопределённые системы линейных уравнений, то есть, имеющие общее решение (об этом - в следующей статье в развитии темы), а, используя метод Крамера, можно лишь констатировать, что система неопределённа;
3. методом Гаусса можно решать системы линейных уравнений, в которых число неизвестных не равно числу уравнений (об этом - также в развитии темы);
4. метод Гаусса основан на элементарных (школьных) методах - методе подстановки неизвестных и методе сложения уравнений, которых мы коснулись в соответствующей статье.

Благодаря этим преимуществам, именно методом Гаусса чаще всего решаются прикладные задачи на сплавы и смеси, стоимость или удельный вес отдельных товаров в группе товаров и другие, в которых системы линейных уравнений применяются для моделирования реальных объектов физического мира. В конце этой статьи мы решим методом Гаусса задачу на сплавы. Кроме того, метод Гаусса является основой одного из методов нахождения обратной матрицы.

Повторяя школьный метод алгебраического сложения уравнений системы, мы выяснили, что к одному из уравнений системы можно прибавлять другое уравнение системы, причём каждое из уравнений может быть умножено на некоторые числа. В результате получаем систему линейных уравнений, эквивалентную данной. В ней уже одно уравнение содержало только одну переменную, подставляя значение которой в другие уравнений, мы приходим к решению. Такое сложение - один из видов элементарного преобразования системы. При использовании метода Гаусса можем пользоваться несколькими видами преобразований.

Пусть дана система линейных уравнений

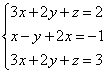
Решая системы линейных уравнений школьными способами, мы почленно умножали одно из уравнений на некоторое число, так, чтобы коэффициенты при первой переменной в двух уравнениях были противоположными числами. При сложении уравнений происходит исключение этой переменной. Аналогично действует и метод Гаусса.

Для упрощения внешнего вида решения составим расширенную матрицу системы:

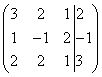
В этой матрице слева до вертикальной черты расположены коэффициенты при неизвестных, а справа после вертикальной черты - свободные члены.

Для удобства деления коэффициентов при переменных (чтобы получить деление на единицу) переставим местами первую и вторую строки матрицы системы. Получим систему, эквивалентную данной, так как в системе линейных уравнений можно переставлять местами уравнения:

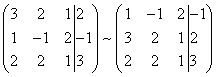
С помощью нового первого уравнения исключим переменную x из второго и всех последующих уравнений. Для этого ко второй строке матрицы прибавим первую, умноженную на 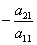(в нашем случае на 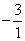), к третьей – первую строку, умноженную на 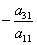(в нашем случае на ).

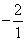Это возможно, так как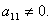

Если бы в нашей системе уравнений было больше трёх, то следовало бы прибавлять и ко всем последующим уравнениям первую строку, умноженную на отношение соответствующих коэффициентов, взятых со знаком минус.

В результате получим матрицу эквивалентную данной системе новой системы уравнений, в которой все уравнения, начиная со второго не содержат