Геометрические фигуры и тела в аксонометрии
Цель: научиться строитьгеометрические фигуры и тела в аксонометрии.
Задание
1. Построить три проекции окружности, вписанные в грани куба, в аксонометрии (прямоугольной изометрии).
2. Построить правильные многогранники в аксонометрии (прямоугольной изометрии и косоугольной фронтальной диметрии).
3. Построить геометрические тела в аксонометрии (призму, пирамиду, цилиндр и конус).
Теоретические сведения
| Рис.1 Аксонометрия модели |
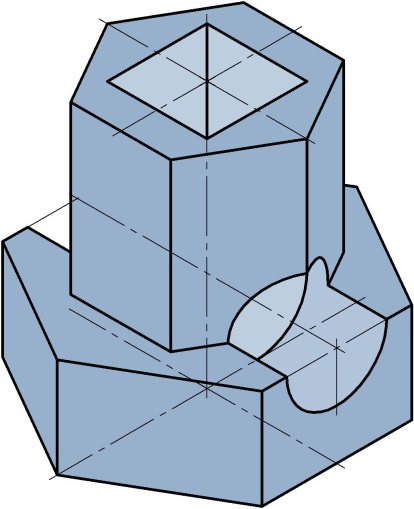 Аксонометрия – это раздел черчения, в котором рассматривается способ получения наглядных объемных изображений предмета на плоскости.
Аксонометрия – это раздел черчения, в котором рассматривается способ получения наглядных объемных изображений предмета на плоскости. Аксонометрические проекции представляют собой наглядное и достаточно точное изображение предметов (рис. 1).
Существует несколько типов аксонометрических проекций. Если проецирующие прямые перпендикулярны аксонометрической плоскости проекции, то такая проекция называется прямоугольной аксонометрической проекцией. К прямоугольным относятся изометрическая и диметрическая проекции.
Если проецирующие прямые направлены не под углом 90° к аксонометрической плоскости проекций, то получают косоугольную аксонометрическую проекцию. К косоугольным относится фронтальная диметрическая проекция.
Мы будем изучать два вида аксонометрических проекций – изометрическую (рис. 2) и косоугольную фронтальную диметрическую (рис. 3), так как они самые простые и часто применяемые.
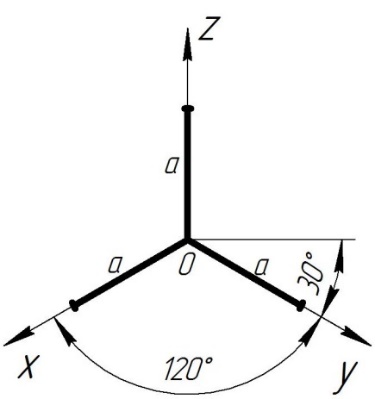 Рис.2Прямоугольная изометрическая проекция Рис.2Прямоугольная изометрическая проекция | 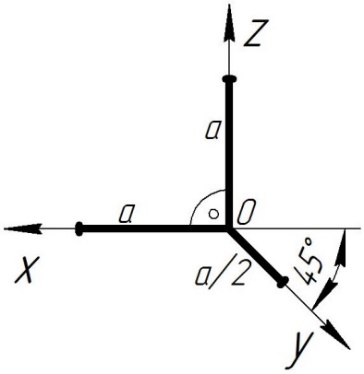 Рис.3Косоугольная фронтальная диметрическая проекция Рис.3Косоугольная фронтальная диметрическая проекция |
Преимущество прямоугольной изометрической проекции в том, что по всем трем осям координаты не искажаются. Именно поэтому проекция была названа греческим словом «изометрия», что в переводе означает равное, равное измерение по осям. При построении этой аксонометрической проекции по осям x, y, z (или линиям, параллельным им) откладывают действительные (натуральные) размеры длины, ширины и высоты предмета.
Для косоугольной фронтальной диметрической проекции коэффициент искажения по оси у – 0,5; по оси х и z искажения нет. При построении этой аксонометрической проекции размеры длины и высоты предмета (отмеряемые по осям х и z либо по прямым, параллельным им) откладываются действительные (натуральные), а размеры ширины предмета (отмеряемые по оси у либо по прямым, параллельным ей) наносятся с уменьшением их величины в два раза.
Получают аксонометрическую проекцию следующим образом. Перед аксонометрической плоскостью (плоскость, на которую проецируют) располагают предмет, помещенный в систему координатных осей. Затем задают направление проецирования и через все точки предмета мысленно проводят проецирующие лучи до пересечения с плоскостью проекции.
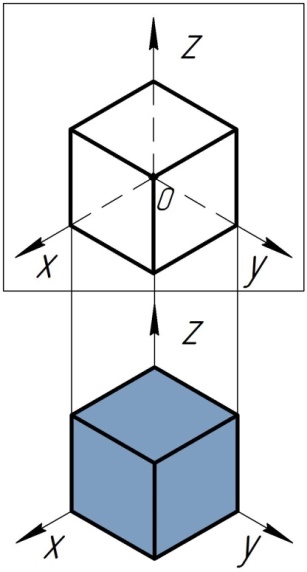 Рис.4 Получение прямоугольной изометрической проекции Рис.4 Получение прямоугольной изометрической проекции | 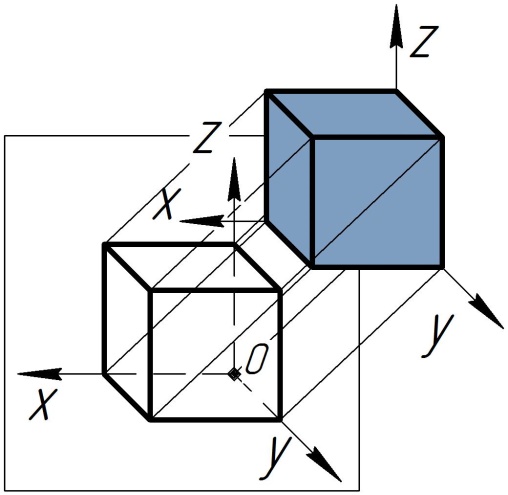 Рис.5 Получение косоугольной фронтальной диметрической проекции Рис.5 Получение косоугольной фронтальной диметрической проекции |
| Помещают объект (куб) в координатный угол, располагают его с одинаковым наклоном граней к аксонометрической плоскости проекций. Через все точки объекта проводят воображаемые параллельные проецирующие лучи под прямым углом к плоскости до пересечения с ней (рис. 4). | Перед плоскостью располагают объект (например, куб) так, чтобы его передняя грань была параллельна плоскости проекций, т.е. фронтально. Параллельные между собой проецирующие лучи направляют под острым углом к плоскости проекций. На аксонометрической плоскости проекций получают изображения координатных осей и косоугольную фронтальную диметрическую проекцию куба (рис. 5). |
В аксонометрических проекциях окружности изображаются с искажениями в виде овалов.
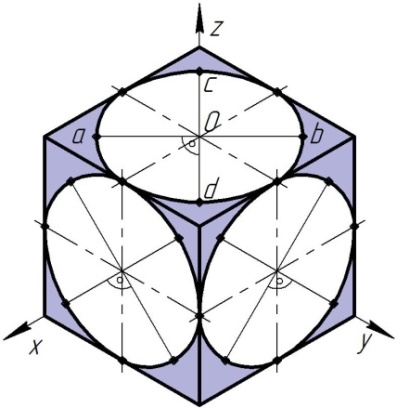
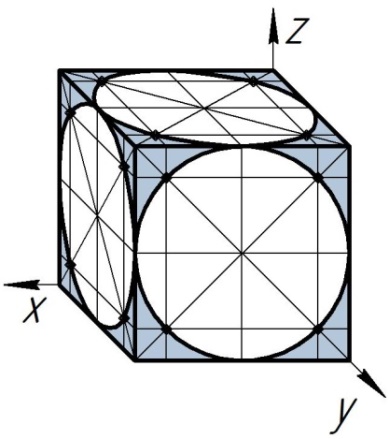
а) б)
Рис.6 Изображение окружностей в аксонометрии: а) – в прямоугольной изометрии; б) – в косоугольной диметрии
Этапы построения овала (рис. 7):
1. Выполняют построение осей аксонометрической проекции;
2. Выполняется аксонометрическое изображение квадрата, описанного вокруг окружности (сторона квадрата равна диаметру окружности);
3. Вписывается в аксонометрию квадрата две дуги, принадлежащие овалу, с помощью циркуля;
4. Выполняются дополнительные построения для нахождения центров и проведения двух других дуг;
5. Производится обводка прямоугольной аксонометрической проекции окружности.
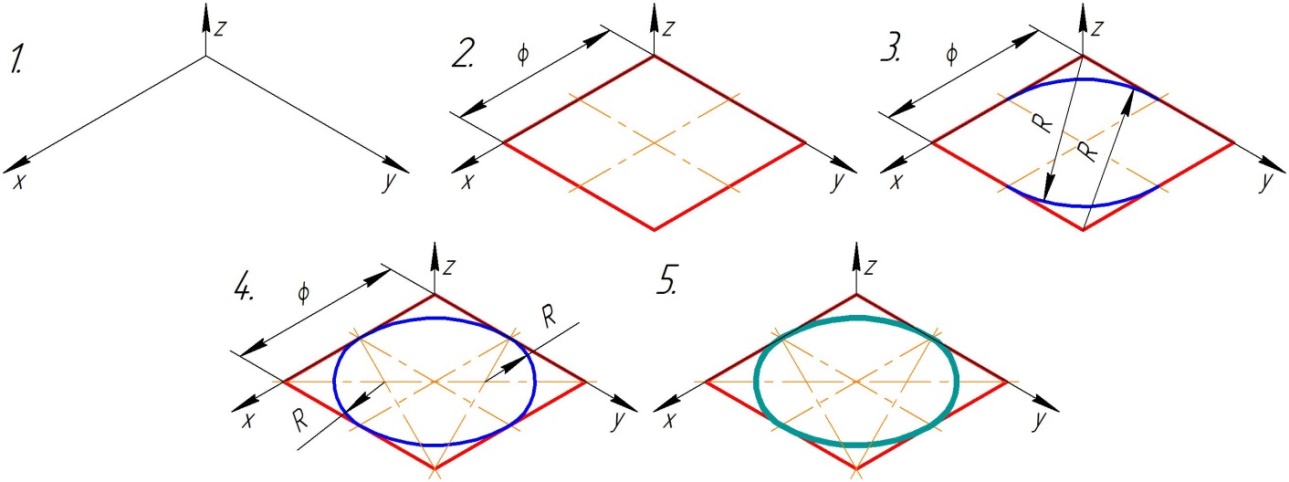
Рис.7Этапы построения овала
Методические рекомендации и порядок выполнения
Для выполнения графического задания требуется изучить построение аксонометрических проекций геометрических фигур и тел.
Работу начать с построения аксонометрии окружности по заданным размерам. Исходные данные и пример выполнения находятся на рис. 8.
Построение аксонометрии плоских фигур выполнить в виде таблицы. Пример оформления – табл. 1.
Построение аксонометрии геометрических тел выполнить в виде таблицы. Пример оформления – табл. 2.
Рис.8 Исходные данные и пример выполнения аксонометрии окружности
Табл.1 Исходные данные и пример выполнения аксонометрии правильных многоугольников
| Правильный многоугольник | Прямоугольная изометрия | Косоугольная диметрия |
Контрольные вопросы:
1.В чем заключается суть аксонометрического проецирования?
2. Дайте характеристику прямоугольной изометрии.
3.Дайте характеристику фронтальной диметрии.
4.Как разделить окружность на пять равных частей ?
5.Опишите построение овалов и эллипсов?
6.В какой аксонометрии нагляднее вычерчивать квадрат, треугольник?
Табл. 2 -Исходные данные и пример выполнения аксонометрии геометрических тел
| Основание геометрического тела | Прямоугольная изометрия | Косоугольная диметрия |
Графическая работа № 3
ПРИЗМА
Цель работы: развить навыки изображения призмы, пересеченной проецирующими плоскостями на проекционном комплексном чертеже и аксонометрии.
Задание
По заданному условию выполнить проекционный комплексный чертеж и аксонометрию призмы со срезами.
Теоретические сведения
Проанализируем чертеж правильной прямой четырехугольной призмы с вырезом по плоскостям αиβсо стороны верхнего основания (рис. 1). Нижнее основание расположено в горизонтальной плоскости.
Призма имеет одну общую плоскость симметрии, проходящую на расстоянии b от фронтальной плоскости проекций, которая будет служить точкой отсчета для координат у. Представим точку зрения в этой плоскости в направлении ^ профильной плоскости проекции.
Можно представить форму призмы в виде каркасной модели (проволочной), образованной боковыми ребрами и ребрами в основании призмы, а так же отрезками, полученными в пересечении боковых граней и верхнего основания с секущими плоскостями. Тогда, каркасная модель призмы включает шесть вертикальных отрезков, шесть горизонтальных, два перпендикулярных к фронтальной плоскости и четыре отрезка в общем расположении (2-3, 3-4, 4-31, 31-21). Если представить поверхностную модель призмы, то она образована четырьмя вертикальными плоскостями (боковые грани), двумя параллельными горизонтальными (основания), одной наклонной αперпендикулярной к фронтальной плоскости и одной профильной β //профильной плоскости проекций, которая как следствие, ^ фронтальнойи горизонтальной. Рекомендуется изобразить каждую прямую и плоскость призмы тремя проекциями. Заметим, что умение начертить каждую отдельную прямую или плоскость на комплексном чертеже, свидетельствует о доскональном представлении формы призмы. Фронтальная и горизонтальная проекции призмы позволяют представить фигуру в объёме и визуализировать её в аксонометрии. В данном случае – косоугольной фронтальной диметрии, как наиболее наглядной. И только после того, как по заданным проекциям будет представлена форма фигуры в пространстве, можно переходить к сознательному построению профильной проекции.
Рис. 1. Построение ПКЧ и аксонометрии правильной четырехугольной призмы
Для начала, в соответствии с условием задачи (основание призмы расположено в горизонтальной плоскости проекции), строим оси x, yи z после совмещения координатных плоскостей в одну из них xОz – фронтальная плоскость. Тогда, плоскость симметрии призмы на профильной проекции будет проходить на расстоянии b от оси z, в которой расположена точка зрения в направлении ^ профильной плоскости проекций.
Профильную проекцию призмы можно построить, получив профильные проекции каждого отрезка, снимая координаты y относительно фронтальной плоскости проекции. Однако в чертежной практике используется так называемый безосный чертеж, когда положение осей не указывается, а отсчет координат y ведется от предметной (локальной) системы координат, которая связана непосредственно с проецируемым объектом. Опираясь на свойство параллельного проецирования о том, что параллельный перенос объекта проецирования относительно плоскости проекции или плоскости проекции относительно объекта проецирования, не влияет на величину и форму самой проекции, тогда расстояния между проекциями устанавливаются исходя из размера формата листа, на котором выполняется чертеж, обеспечения места для нанесения размеров и надписей.
Методические рекомендации
1. Изучить случаи пересечения призмы различными плоскостями.
2. Достроить горизонтальную, профильную и аксонометрическую проекции призмы.
Пример выполнения задания «Призма» приведен на рис. 2.
Варианты заданий приведены в таблице 1.
Таблица 1 – Варианты задания «Призма»
| 1 | 2 | 3 | 4 |
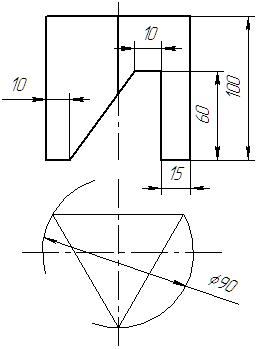 | 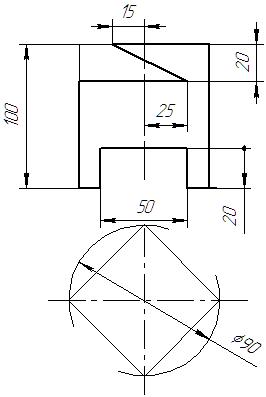 | 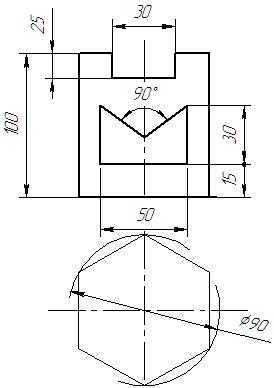 | 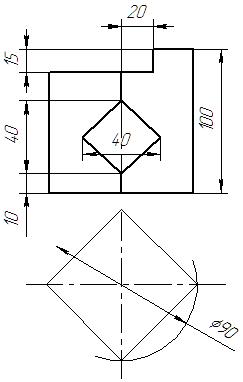 |
Продолжение таблицы 1
| 5 | 6 | 7 | 8 | ||
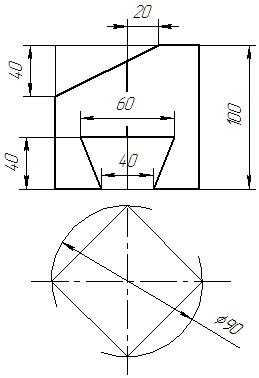 | 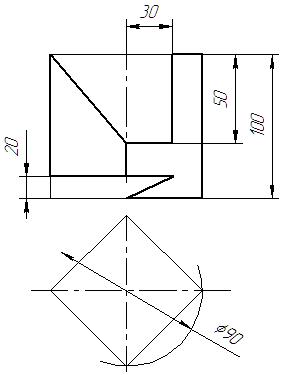 | 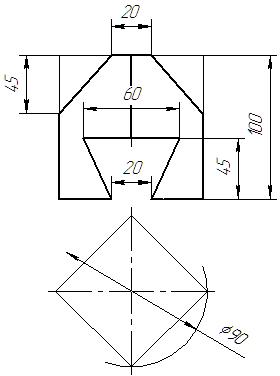 | 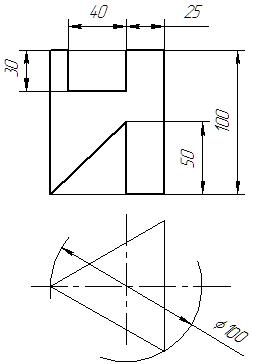 | ||
| 9 | 10 | 11 | 12 | ||
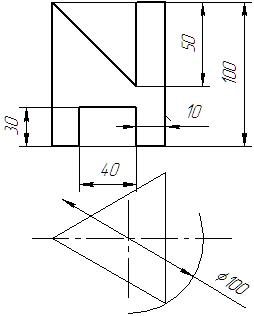 | 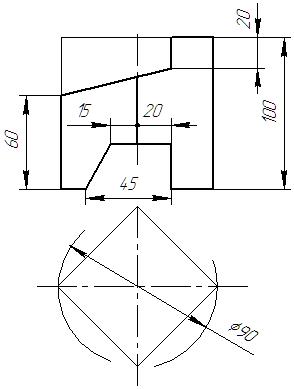 | 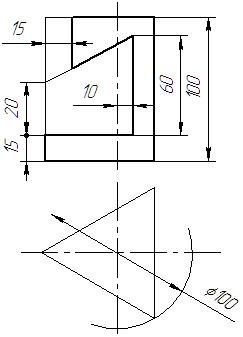 | 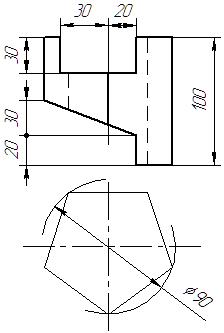 | ||
| 13 | 14 | 15 | 16 | ||
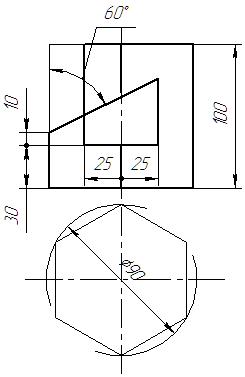 | 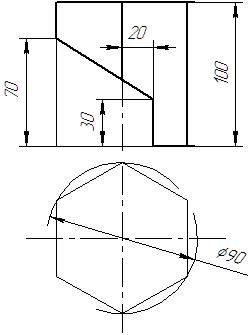 | 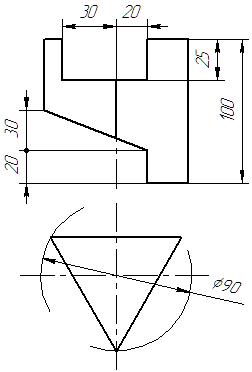 | 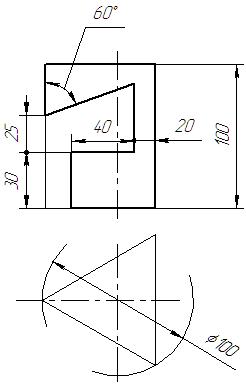 | ||
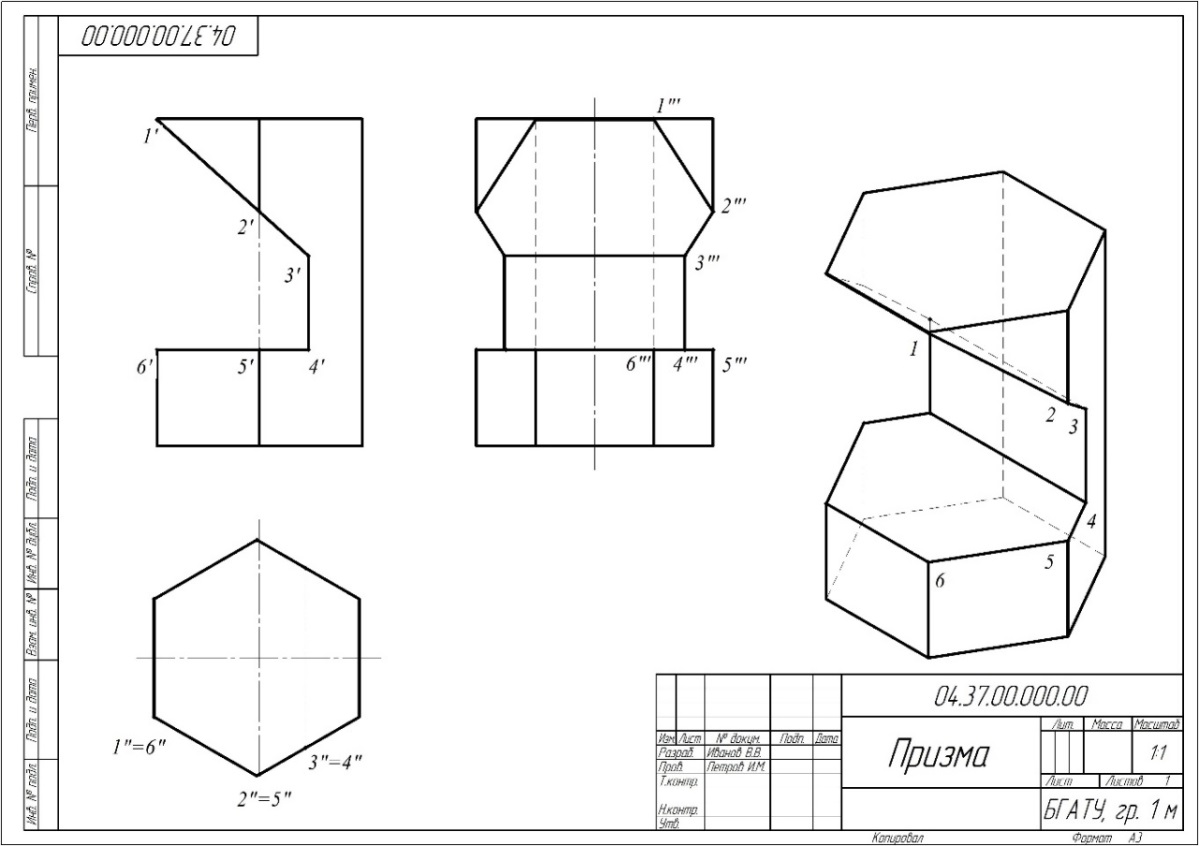
Рис. 2. Пример выполнения задания “Призма”
Контрольные вопросы:
1.Дайте опрделение призмы как геометрического тела.
2.Какая плоская фигура может располагается в основании правильной призмы?
3.Как располагаются основания призмы, расположенные параллельно горизонтальной плоскости проекций, относительно фронтальной плоскости проекций ?
4.Принцип построение точек на поверхности призмы?
5.Сколько граней и ребер в пятиугольной призме?
Графическая работа № 4
ПИРАМИДА
Цель работы: развить навыки изображения пирамиды, пересеченной проецирующими плоскостями на проекционном комплексном чертеже и аксонометрии.
Задание
По заданному условию выполнить проекционный комплексный чертеж и аксонометрию пирамиды со срезами.
Теоретические сведения
На рис. 1 дано построение трех проекций пирамиды с вырезом по фронтально-проецирующим плоскостям αи β.
Для анализа решения задачи, напомним следующую теорему: плоскость, проведенная параллельно основанию пирамиды, рассекает её по фигуре подобной основанию с соответственно параллельными сторонами.
Рис. 1 – Построение ПКЧ и аксонометрии пирамиды
Сначала проанализируем форму заданной пирамиды. Дана правильная прямая треугольная пирамида, основание которой расположено горизонтально. Задняя грань SBC перпендикулярна профильной плоскости проекции. Вырез образован горизонтальной плоскостью α и наклонной плоскостьюβ//SB.На основании вышесказанной теоремы, строим из точки 5 треугольник 547 с соответственно параллельными сторонами (5-4//СА, 4-7//АВ, 7-5//ВС) треугольнику в основании АВС. Затем по линиям связи находим точки 3/и 6/. Точку 1/ отмечаем на ребре S/C/, а точку 2/, используя координату у2 определяем на профильной проекции. Строим профильную проекцию, обратив внимание, что грань SBC на профильной проекции вырождается в отрезок прямой, на которой расположены профильные проекции точек 1,5,6,7 как принадлежащие этой грани. Профильные проекции точек 2и 4,строим исходя из их принадлежности ребру SA.Обратим внимание на параллельность отрезков 2-3 и 1-6 ребру SBпо условию задачи, которые будут соответственно параллельны и на проекциях.
Методические рекомендации
1. Изучить случаи пересечения пирамиды различными плоскостями.
2. Достроить горизонтальную, профильную и аксонометрическую проекции.
Варианты заданий приведены в таблице 1.
Пример выполнения задания «Пирамида» приведен на рисунке 2.
