Положение плоскости относительно плоскости проекций.

Плоскость может занимать различные положения относительно плоскостей проекций. Плоскость, не параллельная и не перпендикулярная ни одной из плоскостей проекций, называется плоскостью общего положения. Задать плоскость на чертеже проекциями множества ее точек практически невозможно, т. к. проекции точек плоскости покроют плоскости проекций и мы не получим на них никаких изображений. Поэтому плоскость на чертеже задают проекциями таких принадлежащих ей геометрических фигур, которые однозначно определяют ее положение в пространстве и позволяют построить любую ее точку.
На основании аксиомы 1 и следствий из нее плоскость общего положения на чертеже можно задать

Плоскости частного положения

а. Проецирующие плоскости
Плоскость, перпендикулярная одной из плоскостей проекций, называется проецирующей.
Горизонтально проецирующая плоскость - плоскость, перпендикулярная П₁ (рис. 2.3.4).
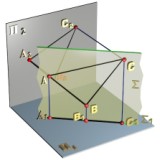Рис. 2.3.4

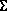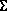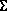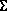
Горизонтальная проекция плоскости вырождается в прямую линию ₁, положение которой соответствует положению плоскости в пространстве ( ₁ = П₁).
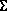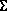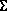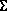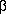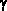Фронтальная проекция плоскости представляет собой множество точек, совпадающее с множеством точек плоскости П₂ ( ₂ = П₂). Горизонтальная проекция любой геометрической фигуры, принадлежащей плоскости , например треугольника АВС, совпадает с горизонтальной проекцией ₁ плоскости . Показанные на рис. 2.3.4 углы и - величины углов наклона плоскости 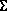соответственно к фронтальной и профильной плоскостям проекций.

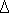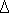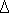
Фронтально проецируюшая плоскость - плоскость, перпендикулярная П₂ (рис. 2.3.5). Фронтальная проекция такой плоскости вырождается в прямую линию ₂, положение которой соответствует положению плоскости в пространстве ( ₂ = П₂). Горизонтальная проекция представляет собой множество точек, совпадающих с множеством точек плоскости П₁ ( 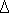₁ = П₁).
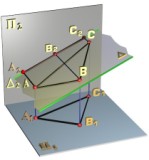Рис. 2.3.5

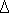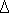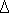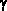Фронтальная проекция любой геометрической фигуры, принадлежащей плоскости , например треугольника ABC, совпадает с фронтальной проекцией ₂ плоскости . Показанные на рис. 2.3.5,б углы и - величины углов наклона плоскости к горизонтальной и профильной плоскостям проекций.
Профильно проецирующая плоскость - плоскость, перпендикулярная П₃, (рис. 2.3.6). Профильная проекция плоскости вырождается в прямую ₃, положение которой соответствует положению плоскости в пространстве (₃ = П₃). Горизонтальная и фронтальная проекции представляют собой множество точек, совпадающих соответственно с множеством точек плоскостей П₁ и П₂.
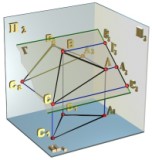Рис 2.3.6.

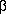Профильная проекция любой геометрической фигуры, принадлежащей плоскости Г, например треугольника АВС, совпадает с профильной проекцией Г₃ плоскости Г. Показанные на рис. 2.3.6 углы и - величины углов наклона плоскости Г к горизонтальной и фронтальной плоскостям проекций.

Плоскости уровня

Плоскость, параллельная одной из плоскостей проекций, называется плоскостью уровня.
Горизонтальная плоскость уровня - плоскость, параллельная П₁ (рис. 2.3.7).
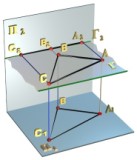Рис 2.3.7

Горизонтальная плоскость уровня Г перпендикулярна плоскостям П₂ и П₃ т. е. является фронтально и профильно проецирующей одновременно и обладает, следовательно, свойствами каждой из них. Любая геометрическая фигура Ф, принадлежащая плоскости Г
(рис. 2.3.7), проецируется на горизонтальную плоскость проекций в конгруэнтную ей фигуру Ф₁, например:

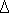ABC 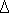A₁B₁C₁ 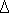ABC

Фронтальная плоскость уровня - плоскость, параллельная П₂ (рис. 2.3.8).
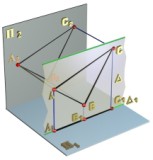Рис 2.3.8

Фронтальная плоскость уровня 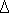перпендикулярна плоскостям
П₁ и П₃ т. е. является горизонтально и профильно проецирующей одновременно и обладает, следовательно, свойствами каждой из них. Любая геометрическая фигура Ф, принадлежащая плоскости 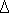, проецируется на фронтальную плоскость проекций в конгруэнтную ей фигуру Ф₂, например;

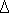ABC 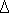A₂B₂C₂ 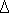ABC

Профильная плоскость уровня - плоскость, параллельная П₃ (рис. 2.3.9).

Рис 2.3.9

Профильная плоскость уровня перпендикулярна плоскостям
П₂, и П₁, т. е. является горизонтально и фронтально проецирующей одновременно и обладает, следовательно, свойствами каждой из них. Любая фигура Ф, принадлежащая плоскости , проецируется на профильную плоскость проекций в конгруэнтную ей фигуру Ф₃, например:

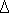ABC A₃B₃C₃ ABC

Главные линии плоскости.

Главные линии плоскости — прямые уровня и линии наибольшего наклона плоскости к плоскостям проекций.

Линии уровня плоскости — прямые, параллельные плоскостям проекций и лежащие в данной плоскости (горизонтали, фронтали, профильные прямые плоскости).

Горизонтали плоскости — прямые, лежащие в плоскости и параллельные горизонтальной плоскости проекций.

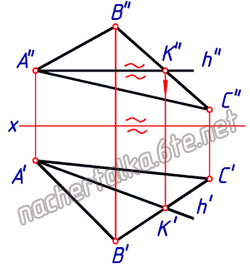
Свойства горизонтали:

— горизонтальная проекция горизонтали параллельна горизонтальной проекции горизонтального следа плоскости;

— фронтальная проекция горизонтали параллельна оси проекций.

Фронтали плоскости — прямые, лежащие в плоскости и параллельные фронтальной плоскости проекций.

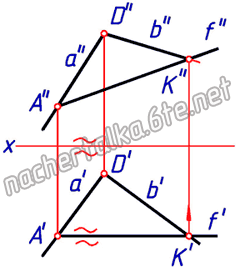
Свойства фронтали:

— фронтальная проекция фронтали параллельна фронтальной проекции фронтального следа плоскости;

— горизонтальная проекция фронтали параллельна оси проекций.

Профильные прямые плоскости — прямые, лежащие в плоскости и параллельные профильной плоскости проекций.

Линии наибольшего наклона плоскости к плоскостям проекций — прямые, лежащие в данной плоскости и перпендикулярные или к горизонталям плоскости, или к её фронталям, или к её профильным прямым. В первом случае определяется угол наклона плоскости к плоскости π1, во втором — к плоскости π2, в третьем — к плоскости π3. Линия наибольшего наклона плоскости к плоскости π1 называется линией ската плоскости.

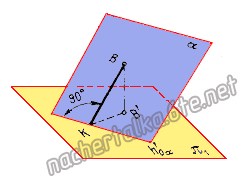
BK — линия ската плоскости α.

Свойства принадлежности.

Основные свойства принадлежности точек и прямых

1 . Какова бы ни была прямая, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие ей.

2 . Через любые две точки можно провести прямую, и только одну.

Основные свойства взаимного расположения точек на прямой и на плоскости

1 Из трех точек на прямой одна и только одна лежит между двумя другими.

2 . Прямая разбивает плоскость на две полуплоскости.

принадлежность прямой плоскости

Сформулируем условие принадлежности прямой плоскости как аксиомы:

Аксиома 1. Прямая принадлежит плоскости, если две её точки принадлежат этой плоскости.

Аксиома 2. Прямая принадлежит плоскости, если имеет с плоскостью одну общую точку и параллельна какой-либо прямой расположенной в этой плоскости.

Проиллюстрируем примерами использование этих аксиом.

Задача. Дана плоскость (n,k) и одна проекция прямой m2 (рис.53).

Требуется найти недостающие проекции прямой m, если известно, что она принадлежит плоскости, заданной пересекающимися прямыми n и k.

Проекция прямой m2 пересекает проекции прямых n2 и k2 в точках В2 и С2 соответственно. Для нахождения недостающих проекций прямой необходимо найти недостающие проекции точек В и С как точек, лежащих на прямых n и k соответственно.

Таким образом, точки В и С принадлежат плоскости, заданной пересекающимися прямыми n и k, а прямая m проходит через эти точки, значит, согласно аксиоме 1, прямая принадлежит этой плоскости.

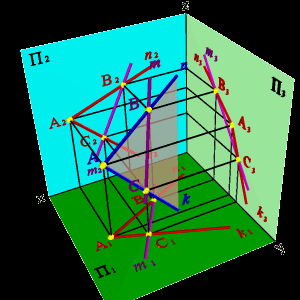
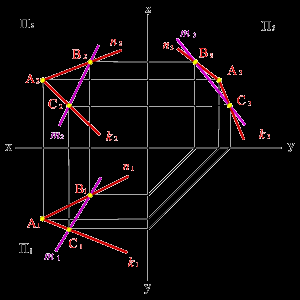
а) модель б) эпюр

Рисунок 53. Прямая и плоскость имеют две общие точки

Задача. Через точку В провести прямую m, если известно, что она принадлежит плоскости заданной пересекающимися прямыми n и k (рис.54).

Пусть точка В принадлежит прямой n, лежащей в плоскости заданной пересекающимися прямыми n и k. Через проекцию В2 проведем проекцию прямой m2 параллельно прямой k2, для нахождения недостающих проекций прямой необходимо построить проекцию точки В1, как точки лежащей на проекции прямой n1 и через неё провести проекцию прямой m1 параллельно проекции k1.

Таким образом, точка В принадлежит плоскости, заданной пересекающимися прямыми n и k, а прямая m проходит через эту точку и параллельна прямой k, значит согласно аксиоме 2 прямая принадлежит этой плоскости.

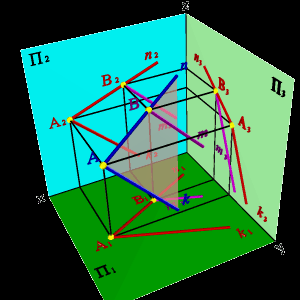
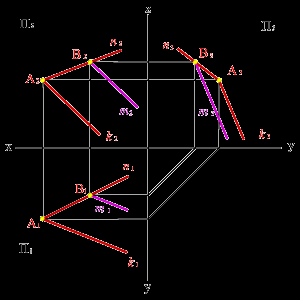
а) модель б) эпюр

Рисунок 54. Прямая имеет с плоскостью одну общую точку и параллельна прямой расположенной в этой плоскости

10.Определение натуральной величины прямой общего положения( 2 способа)

Определение длины отрезка прямой линиии углов наклона прямой к плоскостям проекций.

Длину отрезка АВ можно определить из прямоугольного треугольника АВС |AС|=|A₁B₁|, |BС|= , угол угол наклона отрезка к плоскости П₁, угол наклона отрезка к плоскости П₂. Для этого на эпюре (рис.3.17) из точки B₁ под углом 90⁰ проводим отрезок _₁*, полученный в результате построений отрезок A₁B₁*и будет натуральной величиной отрезка АВ, а угол B₁A₁B₁* =α. Рассмотренный метод называется методом прямоугольного треугольника.

Однако все построения можно объяснить, как вращение треугольника АВСвокруг стороны AС до тех пор, пока он не станет параллелен плоскости П₁, в этом случае треугольник проецируется на плоскость проекций без искажения. Подробнее вращение вокруг оси параллельной плоскости проекций рассмотрены в разделе «Методы преобразования ортогональных проекций»

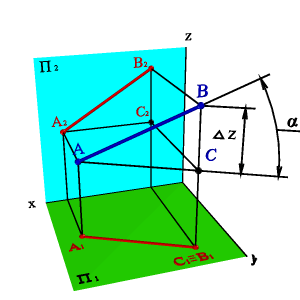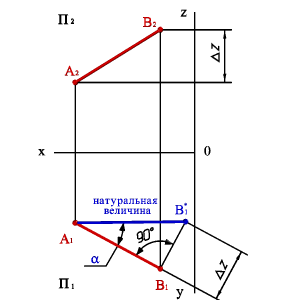а) модель	б) эпюр

Метод замены плоскостей

зменение взаимного положения изучаемого объекта и плоскостей проекций достигается путем замены одной из плоскостей П₁ или П₂ новой плоскостями П₄ (рис. 148). Новая плоскость всегда выбирается перпендикулярно оставшейся плоскости проекций.

Для решения некоторых задач может потребоваться двойная замены плоскостей проекций (рис. 149). Последовательный переход от одной системы плоскостей проекций к другой необходимо осуществлять, выполняя следующее правило: расстояние от новой проекции точки до новой оси должно равняться расстоянию от заменяемой проекции точки до заменяемой оси.

Задача 1: Определить натуральную величину отрезка АВ прямой общего положений (рис. 148). Из свойства параллельного проецирования известно, что отрезок проецируется на плоскость в натуральную величину, если он параллелен этой плоскости.

Выберем новую плоскость проекций П₄, параллельно отрезку АВ и перпендикулярно плоскости П₁. Введением новой плоскости, переходим из системы плоскостей П₁П₂ в систему П₁П₄ , причем в новой системе плоскостей проекция отрезка А₄ В₄ будет натуральной величиной отрезка АВ.

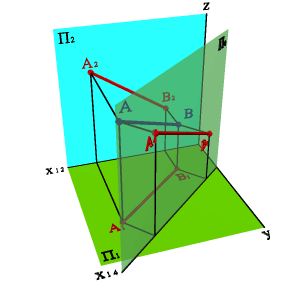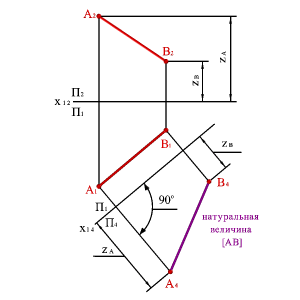а) модель	б) эпюр
Рисунок 148. Определение натуральной величины отрезка прямой методом замены плоскостей проекций

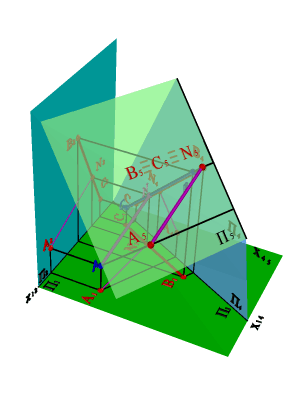
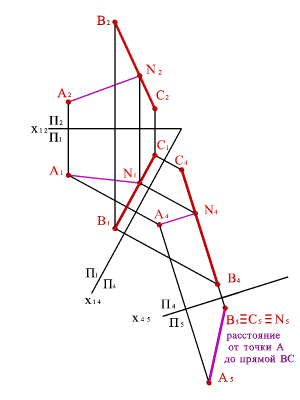
Задача 2: Определить расстояние от точки А до прямой общего положения, заданной отрезком ВС (рис._149).