Взаимно перпендикулярные плоскости.
47. Определить положение прямой m относительно плоскости L.
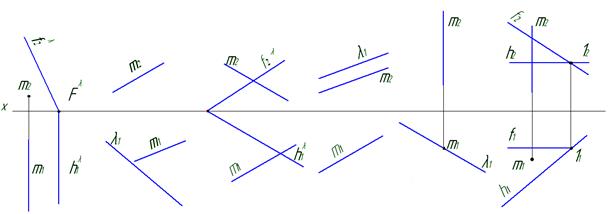
а б в г д е
| а | б | в | г | д | е | |
| Положение прямой относительно плоскости |
48. На каком из чертежей изображена прямая nперпендикулярная плоскости S?
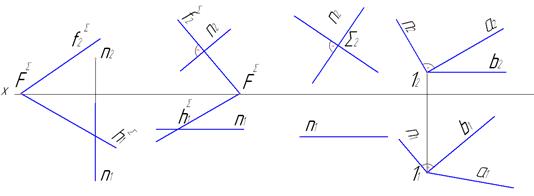
а б в г
| а | б | в | г | |
| Прямая перпендикулярная к плоскости |
49. На каком чертеже плоскости S и L перпендикулярны?
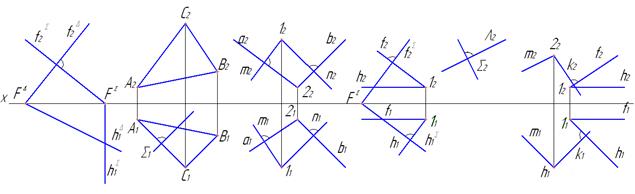
а б в г д е
| а | б | в | г | д | е | |
| Плоскости S и L перпендикулярны |
50. Построить горизонтальную проекцию прямой m, проходящей через точку Апараллельно плоскости L(fxh), а через прямую n провести плоскость S, параллельную прямой d.
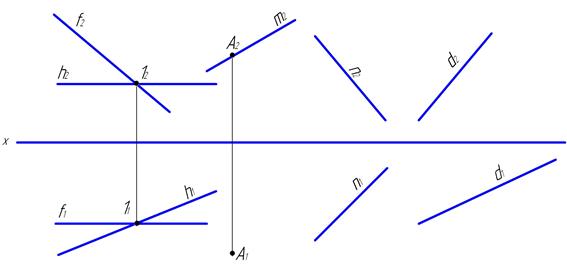
51. Найти точку пересечения, наклонную глубину и элементы залегания буровой скважины, запроектированной в точке А перпендикулярно к слою горной породы. Слой определяется плоскостью S(D, B, C).
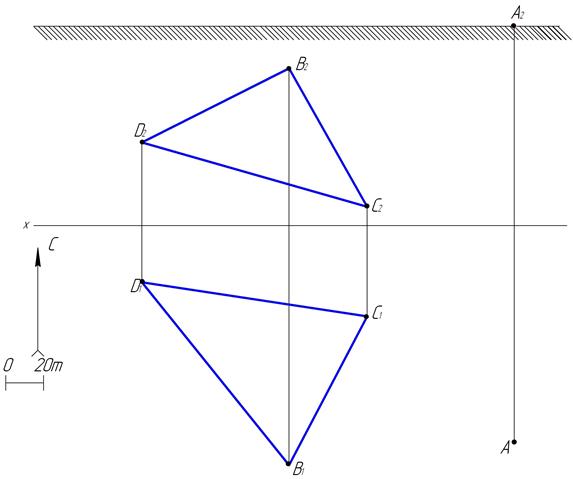
52. На прямой m найти точку, равноудалённую от концов отрезка АВ.
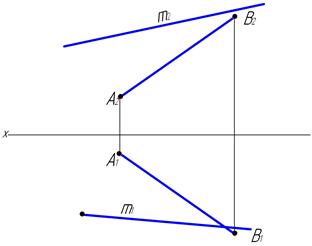
9. Метод перемены плоскостей проекций.
53. Какая координата точки останется неизменной при замене горизонтальной плоскости П1 новой плоскостью проекций П5?
54. Сколько замен плоскостей проекций следует произвести, чтобы прямую общего положения сделать проецирующей?
55. Как следует расположить новую плоскость проекций, чтобы плоскость общего положения сделать проецирующей?
56. Построить проекции точек А, В и С в новых системах плоскостей проекций П2/ П5 и П1 /П4.
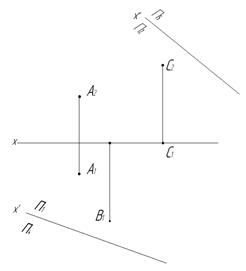
57. Определить расстояние от точки D до плоскости S(А, В, С).
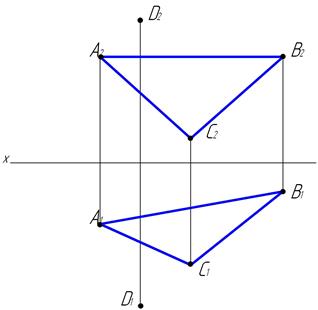
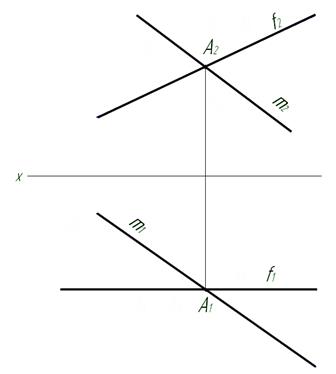
58. Определить истинную величину угла, составленного прямыми m и f.
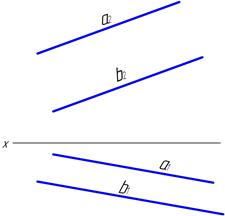
59. Определить кратчайшее расстояние между двумя параллельными прямыми a и b.
10. Метод вращения.
60. Как должна быть расположена ось вращения i, чтобы при вращении вокруг неё: прямая общего положения m заняла бы в пространстве положение, указанное в таблице; плоскость общего положения заняла бы в пространстве положение, указанное в таблице.
| m // P1 | m // P2 | m // P3 | S // P1 | S ^ P1 | S // P2 | S ^ P2 |
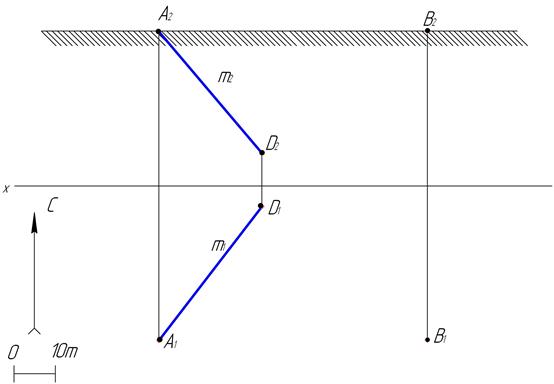
61. Определить истинную величину зенитного угла и наклонную глубину буровой скважины, заданной на чертеже прямой m; в точке В запроектировать скважину с азимутом падения 297° и зенитным углом 35°.
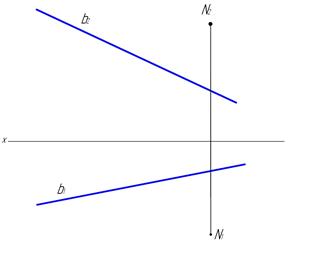
62. Вращением вокруг прямой уровня определить кратчайшее расстояние от точки N до прямой b.
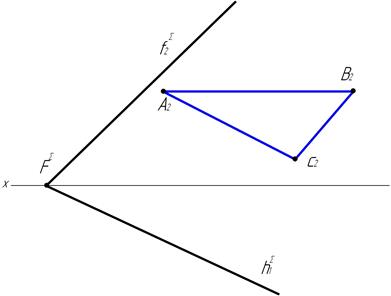
63. Вращением вокруг одного из следов определить истинную величину треугольника АВС, лежащего в плоскости S.
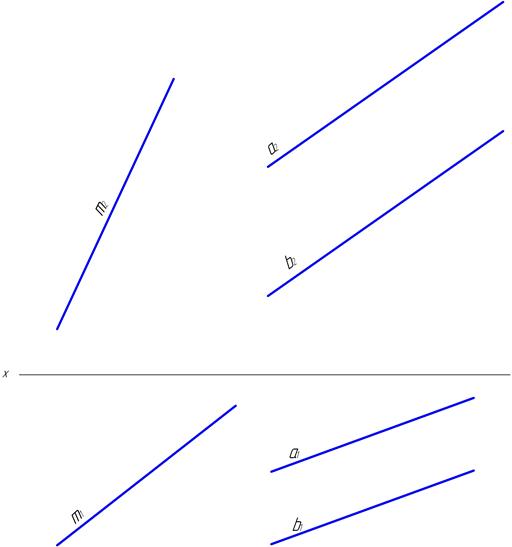
64. Определить угол между прямой m и плоскостью D, заданной параллельными прямыми a и b.
Указания к решению задачи.
Угол между прямой и плоскостью определяется углом m, образованным прямой и её ортогональной проекцией на эту плоскость. Построение проекции угла m требует определения двух точек, первая из которых является точкой пересечения данной прямой m с плоскостью S, а вторая – основанием перпендикуляра, опущенного из произвольной точки на ту же плоскость. В целях сокращения построений необходимо определить угол b, дополняющий до 90° искомый угол m.
Алгоритм.
- из произвольной точки М, принадлежащей прямой m, проводится перпендикуляр n к плоскости D(a//b).
- вращением вокруг прямой уровня определяют угол между прямыми m и n – угол b.
- Вычисляется угол m=90°- b.
11. Многогранники. Пересечение многогранника плоскостью.
