Умножение вектора на число (определение).
БИЛЕТ № 1.
УМНОЖЕНИЕ ВЕКТОРА НА ЧИСЛО (ОПРЕДЕЛЕНИЕ).
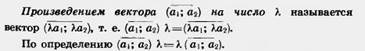 Произведением вектора (а1, а2) на число К называется вектор (kа1, kа2), т. е. (а1, а2) k = { Произведением вектора (а1, а2) на число К называется вектор (kа1, kа2), т. е. (а1, а2) k = { 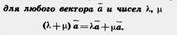 ka1; kа2). По определению (а1, а2) k = k(а1, а2). Из определения операции умножения вектора на число следует, что ka1; kа2). По определению (а1, а2) k = k(а1, а2). Из определения операции умножения вектора на число следует, что 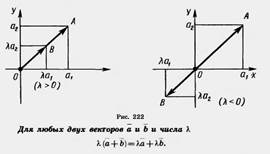 Абсолютная величина вектора Абсолютная величина вектора 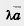 равна равна 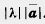 |. Направление вектора |. Направление вектора 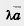 при при 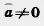 совпадает с направлением вектора совпадает с направлением вектора 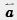 , если , если 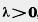 , и противоположно направлению вектора , и противоположно направлению вектора 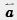 , если , если 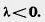 . Абсолютная величина вектора . Абсолютная величина вектора 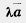 равна: равна: 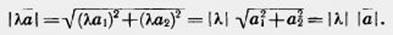 |
ПРИЗНАК ДИАГОНАЛЕЙ ПАРАЛЛЕЛОГРАММ (ДОКАЗАТЕЛЬСТВО).
| Теорема: Если диагонали четырехугольника пересекаются и в точке пересечения делятся пополам, то этот четырехугольник — параллелограмм. | |
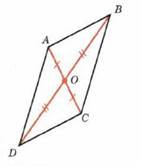 | Дано: АВСD-четырехугольник. АС∩BD=т.О АО=ОС,DО=ОВ |
| Док-ть: АВСD-параллелограмм | |
Доказательство  |
БИЛЕТ№2.
СВОЙСТВА ДИАГОНАЛЕЙ ПАРАЛЛЕЛОГРАММА.
| Теорема: Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам | |
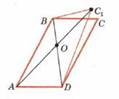 | Дано: АВСD-параллелограмм |
| Док-ть АС∩BD=т.О АО=ОС,DО=ОВ | |
 Доказательство Доказательство |
БИЛЕТ №3.
ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС.
Параллельный перенос — это преобразование плоскости, при котором точки смещаются в одном и том же направлении на одно и то же расстояние. Определение Параллельный перенос — это такое преобразование фигуры F, при котором её произвольная точка (x;y) переходит в точку (x+a; y+b), где a и b — некоторые числа, одинаковые для всех точек (x;y) фигуры F. 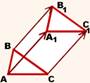 Формулы параллельного переноса Если при параллельном переносе точка A(x;y) переходит в точку A1(x1;y1) Формулы параллельного переноса Если при параллельном переносе точка A(x;y) переходит в точку A1(x1;y1) 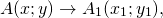 то параллельный перенос задаётся формулами: то параллельный перенос задаётся формулами: 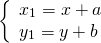 Свойства параллельного переноса 1) Параллельный перенос есть движение (то есть параллельный перенос сохраняет расстояние). 2) При параллельном переносе точки смещаются по параллельным (или совпадающим) прямым на одно и то же расстояние. 3) При параллельном переносе каждая прямая переходит в параллельную ей прямую (или в себя). 4) Каковы бы ни были точки A и A1, существует единственный параллельный перенос, при котором точка A переходит в точку A1. В алгебре параллельный перенос широко используется для построения графиков функций. Свойства параллельного переноса 1) Параллельный перенос есть движение (то есть параллельный перенос сохраняет расстояние). 2) При параллельном переносе точки смещаются по параллельным (или совпадающим) прямым на одно и то же расстояние. 3) При параллельном переносе каждая прямая переходит в параллельную ей прямую (или в себя). 4) Каковы бы ни были точки A и A1, существует единственный параллельный перенос, при котором точка A переходит в точку A1. В алгебре параллельный перенос широко используется для построения графиков функций. |
СВОЙСТВО ПРОТИВОЛЕЖАЩИХ СТОРОН И УГЛОВ ПАРАЛЛЕЛОГРАММА.
| Теорема: У параллелограмма противолежащие стороны равны, противолежащие углы равны | |
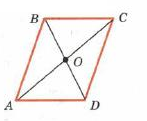 | Дано: АВСD-параллелограмм |
| Док-ть: ВС=АD, АВ=СD, ∟А=∟В=∟С=∟D | |
Доказательство  |
БИЛЕТ№4.
ПОВОРОТ.
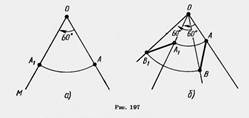 Поворотом на плоскости около данной точки называется такое движение, при котором каждый луч, исходящий из этой точки, поворачивается на один и тот же угол в одном и том же направлении. Поворотом на плоскости около данной точки называется такое движение, при котором каждый луч, исходящий из этой точки, поворачивается на один и тот же угол в одном и том же направлении. 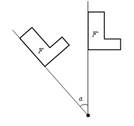 Угол на который поворачивается фигура, относительно точки, называется углом поворота. Угол на который поворачивается фигура, относительно точки, называется углом поворота. |
ПРИЗНАК ПРОТИВОЛЕЖАЩИХ СТОРОН ПАРАЛЛЕЛОГРАММА.
| Теорема: Если у четырехугольника две противолежащие стороны параллельны и равны, то он является паралелограммом | |
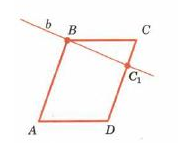 | Дано: АВСD- четырехугольник ВС=АD, АВ=СD, ВС║АD, АВ║СD |
| Док-ть АВСD-. параллелограмм | |
Доказательство  |
БИЛЕТ№5.
БИЛЕТ №6
БИЛЕТ№7.
1.ОПРЕДЕЛЕНИЕ СИНУСА, КОСИНУСА, ТАНГЕНСА И КОСИНУСА ДЛЯ ЛЮБОГО УГЛА ОТ 0° ДО 180°.
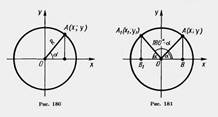 Возьмем окружность на плоскости ху с центром в начале координат и радиусом R (рис. 180). Отложим от положительной полуоси X в верхнюю полуплоскость (полуплоскость, где y>0) угол а. Пусть х и у — координаты точки А. Значения sin а, cos а и tg а для острого угла а выражаются через координаты точки А, а именно: Возьмем окружность на плоскости ху с центром в начале координат и радиусом R (рис. 180). Отложим от положительной полуоси X в верхнюю полуплоскость (полуплоскость, где y>0) угол а. Пусть х и у — координаты точки А. Значения sin а, cos а и tg а для острого угла а выражаются через координаты точки А, а именно: 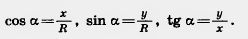 Определим теперь значения sin а, cos а и tg а этими формулами для любого угла а. (Для tg а угол а = 90° исключается.) При таком определении sin 90° = 1, cos 90° = О, sin 180° = О, cos 180° = — 1, tg 180° = 0. Считая, что совпадающие лучи образуют угол 0°, будем иметь: sinO° = 0, cosO° = l, tgO° = 0. Докажем, что для любого угла а, 0°<:а<:180°, sin (180° — а)=sin а, cos (180° — а) = — cos а. Для угла а ^ 90° tg (180° - а) = - tg а. Определим теперь значения sin а, cos а и tg а этими формулами для любого угла а. (Для tg а угол а = 90° исключается.) При таком определении sin 90° = 1, cos 90° = О, sin 180° = О, cos 180° = — 1, tg 180° = 0. Считая, что совпадающие лучи образуют угол 0°, будем иметь: sinO° = 0, cosO° = l, tgO° = 0. Докажем, что для любого угла а, 0°<:а<:180°, sin (180° — а)=sin а, cos (180° — а) = — cos а. Для угла а ^ 90° tg (180° - а) = - tg а. 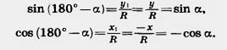 Действительно, треугольники ОАВ и ОА\В\ равны по гипотенузе и острому углу (рис. 181). Из равенства треугольников следует, что АВ=А1В1, т. е. у = у1; ОВ=ОВ1 следовательно, x= —x1. Поэтому разделив почленно равенство sin (180° —а) = sin а на равенство cos (180° — а)=—cos а, получаем: Действительно, треугольники ОАВ и ОА\В\ равны по гипотенузе и острому углу (рис. 181). Из равенства треугольников следует, что АВ=А1В1, т. е. у = у1; ОВ=ОВ1 следовательно, x= —x1. Поэтому разделив почленно равенство sin (180° —а) = sin а на равенство cos (180° — а)=—cos а, получаем: 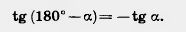 Что и требовалось доказать. Что и требовалось доказать. |
СВОЙСТВА ДИАГОНАЛЕЙ РОМБА.
| Теорема: Диагонали ромба пересекаются под прямым углом. Диагонали ромба являются биссектрисами его углов | |
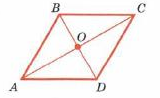 | Дано: АВСD-ромб |
| Док-ть: АС┴BD, АС-биссектриса ∟А и∟С, BD -биссектриса ∟B и∟D | |
Доказательство   |
БИЛЕТ№8.
БИЛЕТ№9.
1.ЗНАЧЕНИЕ СИНУСА, КОСИНУСА, ТАНГЕНСА И КОТАНГЕНСА НЕКОТОРЫХ УГЛОВ (45°, 30°,60°).
Для любого острого угла а sin (90° — а)=cos а, cos (90° — а)=sin а. Доказательство. Пусть ABC — прямоугольный треугольник с острым углом а при вершине А (рис. 160). Тогда острый угол при вершине В равен 90° — а. По определению 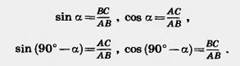 Из второго и третьего равенств получаем sin (90° — а) = cos а. Из первого и четвертого равенств получаем cos (90° — a) = sin а. Теорема доказана. Из второго и третьего равенств получаем sin (90° — а) = cos а. Из первого и четвертого равенств получаем cos (90° — a) = sin а. Теорема доказана. 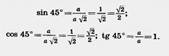 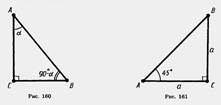 Найдем синус, косинус и тангенс угла 45°. Для этого построим прямоугольный треугольник с острым углом 45° (рис. 161). Второй его острый угол тоже равен 45°, поэтому треугольник равнобедренный. Пусть катеты треугольника равны а. По теореме Пифагора гипотенуза будет Найдем синус, косинус и тангенс угла 45°. Для этого построим прямоугольный треугольник с острым углом 45° (рис. 161). Второй его острый угол тоже равен 45°, поэтому треугольник равнобедренный. Пусть катеты треугольника равны а. По теореме Пифагора гипотенуза будет 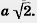 . Находим: . Находим: 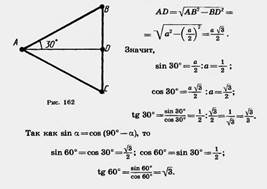 Найдем синус, косинус и тангенс угла 30°. Возьмем равносторонний треугольник ABC (рис. 162). Проведем в нем медиану AD. Она будет биссектрисой и высотой. Поэтому треугольник ABD прямоугольный с острым углом при вершине А, равным 30°. Пусть а — сторона равностороннего треугольника. Тогда BD= Найдем синус, косинус и тангенс угла 30°. Возьмем равносторонний треугольник ABC (рис. 162). Проведем в нем медиану AD. Она будет биссектрисой и высотой. Поэтому треугольник ABD прямоугольный с острым углом при вершине А, равным 30°. Пусть а — сторона равностороннего треугольника. Тогда BD= 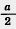 . По теореме Пифагора . По теореме Пифагора |
2.ДОКАЖИТЕ, ЧТО ЕСЛИ ДИАГОНАЛИ ПРЯМОУГОЛЬНИКА ПЕРЕСЕКАЮТСЯ ПОД ПРЯМЫМ УГЛОМ, ТО ОН ЯВЛЯЕТСЯ КВАДРАТОМ.
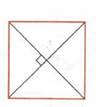 | Дано: АВСD-прямоугольник АС┴BD |
| Док-ть АВСD-квадрат | |
Доказательство  |
БИЛЕТ№10.
1.ОСНОВНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ТОЖДЕСТВА.
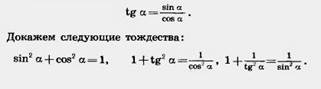 Одно тождество мы уже знаем: Одно тождество мы уже знаем: 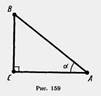 Возьмем любой прямоугольный треугольник ABC с углом при вершине А, равным а. По теореме Пифагора ВС2 + АС2 = АВ2. Разделим обе части равенства на АВ2. Получим: Возьмем любой прямоугольный треугольник ABC с углом при вершине А, равным а. По теореме Пифагора ВС2 + АС2 = АВ2. Разделим обе части равенства на АВ2. Получим: 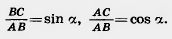 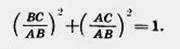 Но . Таким образом,sin2a + cos2 а = 1. Это равенство есть тождество. Оно верно для любого острого угла а. Чтобы получить второе тождество, разделим обе части полученного тождества на cos2 а. Получим: Но . Таким образом,sin2a + cos2 а = 1. Это равенство есть тождество. Оно верно для любого острого угла а. Чтобы получить второе тождество, разделим обе части полученного тождества на cos2 а. Получим: 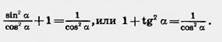 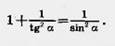 Если обе части тождества sin2 а + cos2а = 1 разделить на sin2а, то получим третье тождество : Значение этих тождеств заключается в том, что они позволяют, зная одну из величин sin а, cos а или tg а, найти две другие. Если обе части тождества sin2 а + cos2а = 1 разделить на sin2а, то получим третье тождество : Значение этих тождеств заключается в том, что они позволяют, зная одну из величин sin а, cos а или tg а, найти две другие. |
ТЕОРЕМА ФАЛЕСА.
| Теорема: Если параллельные прямые отсекают на одной стороне угла равные отрезки, то они отсекают равные отрезки и на другой его стороне. | |
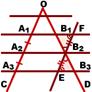 | Дано: ∟COD A1B1 ∥ A2B2 ∥ A3B3, A1, A2, A3 ∈ OC, B1, B2, B3 ∈ OD, A1A2=A2A3. |
| Док-ть B1B2=B2B3. | |
| Доказательство 1) Через точку B2 проведем прямую EF, EF ∥ A1A3. 2) Рассмотрим четырехугольник A1FB2A2. - A1F ∥ A2B2 (по условию), - A1A2 ∥ FB2 (по построению).Следовательно, A1FB2A2 — параллелограмм (по определению). По свойству противолежащих сторон параллелограмма, A1A2=FB2. 3) Аналогично доказываем, что A2B2EA3 — параллелограмм и A2A3=B2E. 4) Так как A1A2=A2A3 (по условию), то FB2=B2E. 5) Рассмотрим треугольники B2B1F и B2B3E. - FB2=B2E (по доказанному), - ∠B1B2F=∠B2EB3 (как вертикальные), - ∠B2FB1=∠B2EB3 (как внутренние накрест лежащие при A1B1 ∥ A3B3 и секущей EF). Следовательно, треугольники B2B1F и B2B3E равны (по стороне и двум прилежащим к ней углам). Из равенства треугольников следует равенство соответствующих сторон: B1B2=B2B3. Что и требовалось доказать. |
Билет№11.
1.СООТНОШЕНИЕ МЕЖДУ СТОРОНАМИ И УГЛАМИ В ПРЯМОУГОЛЬНОМ ТРЕУГОЛЬНИКЕ (ОПРЕДЕЛЕНИЕ).
 |
2.ДОКАЗАТЬ ТЕОРЕМУ О СРЕДНЕЙ ЛИНИИ ТРАПЕЦИИ.
Теорема:  | |
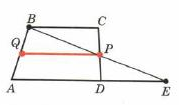 | Дано: ΔАВСД-данная трапеция QP-средняя линия |
| Док-ть QP║ BC, QP║AD QP =1/2 (BC+ AD) | |
Доказательство   |
Билет№12.
1.ПЕРПЕНДИКУЛЯР И НАКЛОННАЯ (ОПРЕДЕЛЕНИЕ).
 |
2. ДОКАЖИТЕ,ЧТО СЕРЕДИНЫ СТОРОН ЧЕТЫРЕХУГОЛЬНИКА ЯВЛЯЮТСЯ ВЕРШИНАМИ ПАРАЛЛЕЛОГРАММА.
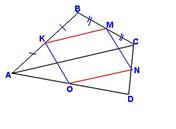 | Дано: ΔАВС-треугольник ЕД-средняя линия |
| Док-ть ЕД║АВ,ЕД=1/2АВ | |
| Доказательство: Проведем диагональ АС в четырехугольнике АВСД.АС разбивает четырехугольник на 2 треугольника АВС и АДС. Проведем средние линии в треугольниках КМ и ОN. КМ - средняя линия ΔАВС(по определению), тогда КМ = АС/2 и КМ ║ АС. ON- средняя линия ΔADC, значит ON = AC/2 и ON ║АС Получаем, что KM=ON и KM параллельна ON(это признак!) Если две стороны четырехуг. равны и параллельны, то четырехуг. - параллелограмм. Значит KMNO параллелограм. |
Билет№13.
1.СИНУС, КОСИНУС И ТАНГЕНС ОСТРОГО УГЛА ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА (ОПРЕДЕЛЕНИЕ).
 |
2.ДОКАЗАТЬ ТЕОРЕМУ О СРЕДНЕЙ ЛИНИИ ТРЕУГОЛЬНИКА.
Теорема:  | |
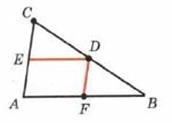 | Дано: ΔАВС-треугольник ЕД-средняя линия |
| Док-ть ЕД║АВ,ЕД=1/2АВ | |
Доказательство  |
Билет№14.
Билет№15.
1. ОПРЕДЕЛЕНИЕ ТРАПЕЦИИ. ВИДЫ ТРАПЕЦИИ.
 Все трапеции можно разделить на три вида: - равнобедренные трапеции; - прямоугольные трапеции; - произвольные трапеции. Равнобедренные трапеции — это трапеции, у которых боковые стороны равны. Прямоугольные трапеции — это трапеции, у которых одна боковая сторона перпендикулярна основаниям. Произвольные трапеции — все остальные трапеции, которые не являются ни равнобедренными, ни прямоугольными. Схематически виды трапеций можно изобразить так: Все трапеции можно разделить на три вида: - равнобедренные трапеции; - прямоугольные трапеции; - произвольные трапеции. Равнобедренные трапеции — это трапеции, у которых боковые стороны равны. Прямоугольные трапеции — это трапеции, у которых одна боковая сторона перпендикулярна основаниям. Произвольные трапеции — все остальные трапеции, которые не являются ни равнобедренными, ни прямоугольными. Схематически виды трапеций можно изобразить так:  |
Билет№16.
1. ОПРЕДЕЛЕНИЕ КВАДРАТА. СВОЙСТВА КВАДРАТА.
 |
2.ТЕОРЕМА ПИФАГОРА (ДОКАЗАТЕЛЬСТВО).
Теорема:  | |
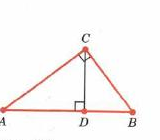 | Дано: ΔАВС-прямоугольный треугольник ∟С= 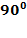 |
Док-ть 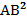 = = 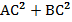 | |
Доказательство  |
Билет№17.
1. ОПРЕДЕЛЕНИЕ РОМБА. СВОЙСТВА РОМБА.
  |
2.НЕРАВЕНСТВО ТРЕУГОЛЬНИКА (ДОКАЗАТЬ ТЕОРЕМУ).
Теорема:  | |
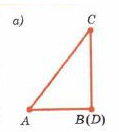 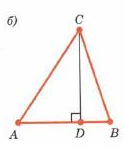 | Дано: А,В,С-данные точки |
Док-ть 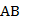 < < 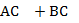 | |
Доказательство   |
Билет№18.
Билет№19.
1 .ОПРЕДЕЛЕНИЕ ЧЕТЫРЕХУГОЛЬНИКА.
 |
2.СЛОЖЕНИЕ ВЕКТОРОВ (ДОКАЗАТЕЛЬСТВО).ПРАВИЛО ТРЕУГОЛЬНИКА И ПРАВИЛО ПАРАЛЛЕЛОГРАММА (РАССМОТРЕТЬ СПОСОБЫ ПОСТРОЕНИЯ).

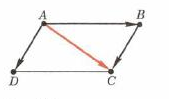

Билет№20.
1.ОПРЕДЕЛЕНИЕ И СВОЙСТВА ПАРАЛЛЕЛОГРАММА.
   |
 2. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ (ОПРЕДЕЛЕНИЕ). ДОКАЗАТЬ ТЕОРЕМУ О СКАЛЯРНОМ ПРОИЗВЕДЕНИИ ВЕКТОРОВ.
2. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ (ОПРЕДЕЛЕНИЕ). ДОКАЗАТЬ ТЕОРЕМУ О СКАЛЯРНОМ ПРОИЗВЕДЕНИИ ВЕКТОРОВ.

БИЛЕТ № 1.
УМНОЖЕНИЕ ВЕКТОРА НА ЧИСЛО (ОПРЕДЕЛЕНИЕ).
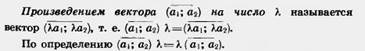 Произведением вектора (а1, а2) на число К называется вектор (kа1, kа2), т. е. (а1, а2) k = { Произведением вектора (а1, а2) на число К называется вектор (kа1, kа2), т. е. (а1, а2) k = { 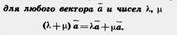 ka1; kа2). По определению (а1, а2) k = k(а1, а2). Из определения операции умножения вектора на число следует, что ka1; kа2). По определению (а1, а2) k = k(а1, а2). Из определения операции умножения вектора на число следует, что  Абсолютная величина вектора Абсолютная величина вектора 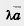 равна равна 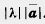 |. Направление вектора |. Направление вектора 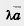 при при 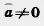 совпадает с направлением вектора совпадает с направлением вектора 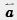 , если , если 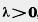 , и противоположно направлению вектора , и противоположно направлению вектора 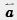 , если , если 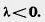 . Абсолютная величина вектора . Абсолютная величина вектора 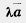 равна: равна: 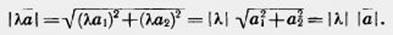 |
