Расчетно-графическая работа № 5
«Определение надежности системы с использованием формулы Байеса и построение деревьев отказов»
Теоретическая часть
Все задачи в теории надежности преобразовать к параллельному и последовательному соединению невозможно. Имеются комбинации элементов, которые в смысле надежности не являются ни последовательными, ни параллельными.
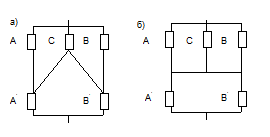
Рис. 5.1 Схемы соединения элементов
На рис. 5.1 приведены схемы соединения элементов. Два одинаковых канала 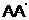 и
и 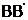 включены параллельно так, что если один из них исправен, то на выходе нет отказов. Если блоки
включены параллельно так, что если один из них исправен, то на выходе нет отказов. Если блоки 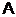 и
и 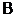 недостаточно надежны, то вводится третий элемент
недостаточно надежны, то вводится третий элемент 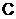 таким путем, что он может снабжать сигналом
таким путем, что он может снабжать сигналом 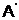 и
и 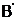 .
.
В случае рис. 5.1.б каждый элемент 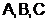 может работать самостоятельно, как с
может работать самостоятельно, как с 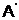 , так и с
, так и с 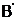 . Возможна работа в следующих комбинациях:
. Возможна работа в следующих комбинациях: 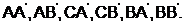 Данная система состоит из элементов, соединенных между собой последовательно – параллельно. Вероятность безотказной работы будет определяться по формулам (4.1 - 4.5). Выражение примет вид:
Данная система состоит из элементов, соединенных между собой последовательно – параллельно. Вероятность безотказной работы будет определяться по формулам (4.1 - 4.5). Выражение примет вид:
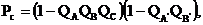 | (5.1) |
В случае, представленном на рис. 5.1.а, предполагается работа только 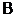 и
и 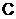 с
с 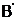 и
и 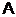 и
и 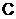 с
с 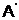 . Обратная связь
. Обратная связь 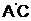 и
и 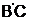 невозможна. Надежность такой системы будет определяться, исходя из формулировки теоремы Байеса: если
невозможна. Надежность такой системы будет определяться, исходя из формулировки теоремы Байеса: если 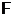 - событие, зависящее от одного из двух несовместных событий
- событие, зависящее от одного из двух несовместных событий 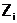 и
и 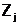 , из которых хотя бы одно обязательно произойдет, то вероятность появления события
, из которых хотя бы одно обязательно произойдет, то вероятность появления события 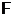 равна:
равна:
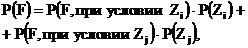 | (5.2) |
Если принять, что 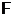 - это отказ системы, а
- это отказ системы, а 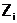 и
и 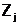 - соответственно безотказная работа и отказ некоторого элемента или блока от которого зависит надежность системы (в данном случае таким является элемент
- соответственно безотказная работа и отказ некоторого элемента или блока от которого зависит надежность системы (в данном случае таким является элемент 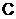 ), то формула определения надежности системы, приведенной на рис. 5.1.а, примет вид:
), то формула определения надежности системы, приведенной на рис. 5.1.а, примет вид:
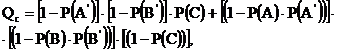 | (5.3) |
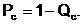 | (5.4) |
Данная формула меняет свой вид в зависимости от схемы соединения элементов.
Для анализа надежности описанных технических систем используют деревья отказов. Целью построения деревьев отказов является символическое представление последовательности возникновения условий, приводящих систему к отказу, нежелательному (критическому) для объекта в целом.
Построение дерева отказов для сложной системы предполагает четкое представление о всех функциональных взаимосвязях элементов, причинах их отказов, а также о последствиях этих отказов. Первое из перечисленного получают посредством построения структурно-функциональной схемы (построение схемы соединения). Затем выстраивается дерево отказов технической системы.
Для построения дерева отказов разработана специальная символика (табл. 5.1). Вершиной дерева является конечное событие - полный отказ системы. Промежуточные вершины (узлы) представляют собой логические операции типа И и ИЛИ, соответствующие описанию языка бинарной логики [3, 4]
Таблица 5.1
Основные обозначения, используемые при построении деревьев отказов
| Вид элемента | Наименование | Описание |
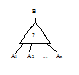 | Схема И | Выходной сигнал В появляется только тогда, когда поступают все входные сигналы (А1 Ç А2 Ç ... Ç Аn) Þ В |
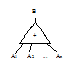 | Схема ИЛИ (объединение) | Выходной сигнал В появляется при поступлении любого одного или большего числа сигналов Аi (А1 È А2 È ... È Аn) Þ В |
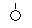 | Первичный отказ | |
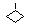 | Неполное событие | Отказ (неисправность), причины которого выявлены не полностью, например, из-за отсутствия информации |
 | Ожидаемое событие | Отказ, появление которого ожидается |
После того, как дерево отказов системы построено, производят его качественный и количественный анализ и вычисляют вероятность результирующего полного отказа системы с учетом известной информации о надежности элементов.
ЗАДАНИЕ
Рассчитать надежность системы представленной на рис. 5.2 и построить дерево отказов при условии, что элемент С неисправен. Сделать вывод. Схемы соединения и исходные данные для расчета представлены в табл. 5.2.
Таблица 5.2
Исходные данные для расчета
1 Вариант 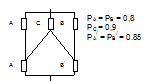 | 2 Вариант 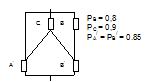 |
3 Вариант  | 4 Вариант 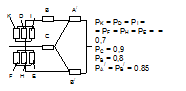 |
Примечание: Номер варианта соответствует номеру подгруппы студентов (устанавливается преподавателем).
Задания для самоконтроля
1. Назначение деревьев отказов.
2. Логические обозначения при построении деревьев отказов.
3. Схемы соединения элементов не являющиеся ни последовательными ни параллельными в смысле надежности.
4. Формулировка теоремы Байеса.
5. Расчет надежности технической системы с использованием формулы Байеса.
Литература
1. Базовский И. Надежность. Теория и практика. М.: Мир, 1965.
2. Машиностроение. Энциклопедия в сорока томах. Т. IV. Надежность машин /Под. ред. К.С. Колесникова. М.: Машиностроение, 1998.
3. Диллан Б., Сингх Ч. Инженерные методы обеспечения надежности систем: Пер. с анг. М.: Мир, 1984.
4. Райншке К., Ушаков И.А. Оценка надежности систем с использованием графов. М.: Радио и связь, 1988.
