Концепция риска и методы его оценки
ПРИНЯТИЕ РЕШЕНИЙ
ПО ФИНАНСОВЫМ ИНВЕСТИЦИЯМ
Методические рекомендации
Для проведения практических занятий
Волгоград 2013
Принятие решений по финансовым инвестициям: Методические указания для практических занятий/Сост. Н. В. Шапошникова; Волгогр. гос. Агр. Универс. Волгоград, 2013, 32 с.
Изложены содержание и порядок использования новых финансовых инструментов, методика оценки их доходности, измерения риска.
Предназначается для студентов экономических специальностей, слушателей ФПК, научных и практических работников.
Цель занятий состоит в обучении студентов методике определения и использования традиционных и новых финансовых инструментов, оценки их доходности, измерения риска в условиях рыночной экономики.
Исходная информация для сравнительного анализа
Уровня финансового левериджа
| Показатель | Доля заемного капитала в общей сумме долгосрочных источников средств (структура капитала) | ||
| 0 % | 25 % | 50 % | |
| Собственный капитал Заемный капитал Общая сумма капитала Годовые расходы за пользование заемным капиталом: % сумма | - |
6. Новые инструменты долгосрочного финансирования
Задача № 1
Уставной капитал акционерного общества составляет 100 тыс. акций. Общество планирует дополнительно выпустить 20 тыс. акций. Каждый акционер получает право на приобретение новых акций пропорционально его доле. Например, владелец 1000 акций получает право на приобретение одной сотой нового выпуска, т. е. двухсот акций. Определить уставной капитал и долю акций акционера.
Задача № 2
Рассчитать цену «права на покупку» в условиях предыдущего примера, если:
а) акции дают право на покупку новых акций (т. е. продаются с правом покупки) и продаются по цене 2600 р.;
б) акции продаются по той же цене 2600 р., но без права покупки новых акций.
Задача № 3
Компания А приобрела трехмесячный опцион покупателя у компании Б на 100 акций с ценой исполнения 1600 р. Цена контракта - 20000 р. Определить: а) доход покупателя; б) доход или убыток, если курсовая цена составит интервал (1600 р. - 1800 р.).
Содержание
1. Концепция риска и методы его оценки ……………………………………...………3
2. Оценка риска инвестиционного портфеля..................................................................6
3. Модель оценки доходности финансовых активов …………… ………………..…8
4. Определение стоимости инвестиционных инструментов ……………………..….11
5. Леверидж, его роль в инвестиционной деятельности ………...………..………... 13
6. Новые инструменты долгосрочного, финансирования…………………..............19
7. Практические задания…………………………………………………......………...22
ПРИНЯТИЕ РЕШЕНИЙ
ПО ФИНАНСОВЫМ ИНВЕСТИЦИЯМ
Методические рекомендации
Для проведения практических занятий
Волгоград 2013
Принятие решений по финансовым инвестициям: Методические указания для практических занятий/Сост. Н. В. Шапошникова; Волгогр. гос. Агр. Универс. Волгоград, 2013, 32 с.
Изложены содержание и порядок использования новых финансовых инструментов, методика оценки их доходности, измерения риска.
Предназначается для студентов экономических специальностей, слушателей ФПК, научных и практических работников.
Цель занятий состоит в обучении студентов методике определения и использования традиционных и новых финансовых инструментов, оценки их доходности, измерения риска в условиях рыночной экономики.
Концепция риска и методы его оценки
Риск и доходность в финансовом менеджменте и анализе рассматриваются как две взаимосвязанные категории. Они могут быть ассоциированы как с каким-либо отдельным видом финансовых активов, так и с их комбинацией .
Существуют различные определения понятия «риск». Так, в наиболее общем виде под риском понимают вероятность возникновения убытков или недополучения доходов по сравнению с прогнозируемым вариантом. Можно сформулировать и более детализированные подходы к определению этого понятия. В частности, риск может быть определен как уровень конкретной финансовой потери, выражающийся: а) в возможности не достичь поставленной цели; б) неопределенности прогнозируемого результата; в) субъективности оценки прогнозируемого результата. Мы будем рассматривать риск в отношении финансовых активов; кроме того, позднее будут рассмотрены другие виды риска в отношении деятельности компании в целом и управления инвестиционными проектами.
Активы, с которыми ассоциируется относительно большой размер возможных потерь, рассматриваются как более рисковые; вполне естественно, что к таким активам предъявляются и большие требования в отношении доходности.
Доход, обеспечиваемый каким-либо активом, состоит из двух компонентов: полученных дивидендов и дохода от изменения стоимости актива. Доход, исчисленный в процентах к первоначальной стоимости актива, называется доходностью данного актива, или нормой прибыли. Доход - абсолютный показатель, его можно суммировать в пространстве и времени; доходность - показатель относительный, и здесь такого суммирования делать уже нельзя.
Количественно риск может быть охарактеризован как некий показатель, измеряющий вариабельность дохода или доходности. Таким образом, очевидный вывод состоит в том, что, как показано в курсе экономической статистики, для этой цели можно использовать ряд статистических коэффициентов, в частности: размах вариации, дисперсию, среднее квадратическое отклонение, называемое иногда стандартным, и коэффициент вариации. Дадим краткую характеристику этим показателям, имея в виду, что в случае необходимости читатель может найти более подробную информацию по этому вопросу в любом стандартном учебнике по общей теории статистики.
Рассмотрим ряд статистических величин (это могут быть как абсолютные, так и относительные величины):
Х1, Х2,X3, ..., Хn.
Размахом вариации называется разность между максимальным и минимальным значениями признака данного ряда:
R=Хmax — Хmin . (1.1)
Этот показатель имеет много недостатков. Во-первых, он дает грубую оценку степени вариации значений признака. Во-вторых, он является абсолютным показателем и потому его применение в сравнительном анализе весьма ограничено. В-третьих, его величина слишком зависит от крайних значений ранжированного ряда.
Дисперсия является средним квадратом отклонений значений признака от его средней и рассчитывается по формуле:
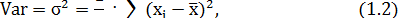
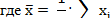
Среднее квадратическое отклонение показывает среднее отклонение значений варьирующего признака относительно центра распределения, в данном случае - средней арифметической. Этот показатель рассчитывается по формуле:
σ = 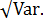 (1.3)
(1.3)
Все вышеприведенные показатели обладают одним общим недостатком- это абсолютные показатели, значения которых существенно зависят от абсолютных значений исходного признака ряда. Поэтому большее применение имеет коэффициент вариации, рассчитываемый по формуле:
CV = 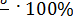 (1.4)
(1.4)
Необходимо отметить еще одну очень важную особенность анализа риска и доходности. Как и любая вероятностная категория, риск может быть оценен по-разному. Однако речь должна идти не только и не столько о различии в алгоритмах и критериях оценки, приведенных выше, сколько о том, рассматривается ли данный финансовый актив изолированно или как составная часть набора активов.
При рассмотрении актива изолированно никаких особых проблем теоретического характера в принципе не возникает, а его рисковость может быть измерена с помощью одной из рассмотренных выше статистик. Тем не менее, как и в любом перспективном анализе, инвестор в этом случае сталкивается с одной проблемой, а именно: с проблемой оценки ожидаемых значений исходных параметров. В частности, какой бы мерой инвестор не пользовался, ему необходимо оценить ожидаемую доходность актива. Чаще всего делают три оценки: пессимистическую (kр), наиболее вероятную (kml) и оптимистическую (ko). Безусловно, число исходов может быть увеличено, однако степень разумной достоверности ожидаемых значений доходности и вероятностей их осуществления при этом, естественно, снизится.
Если ограничиваются тремя оценками, то наиболее общей мерой риска, ассоциируемого с данным активом, может служить размах вариации ожидаемой доходности, рассчитываемый по формуле:
R = ko – kp. (1.5)
Можно рассчитать и другие меры риска, основанные на построении вероятностного распределения значений доходности и исчислении стандартного отклонения от средней доходности и коэффициента вариации, которые и рассматриваются как степень риска, ассоциируемого с данным активом. Таким образом, чем выше коэффициент вариации, тем более рисковым является данный вид актива. Последовательность аналитических процедур в этом случае такова:
а) делаются прогнозные оценки значений доходности (kj) и вероятностей их осуществления (Рj), i = 1,...n, где n - число исходов;
б) рассчитывается наиболее вероятная доходность (kml):

в) рассчитывается стандартное отклонение (σ):
σ = 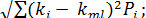 (1.7)
(1.7)
г) рассчитывается коэффициент вариации (CV):
CV = 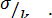 (1.8)
(1.8)
