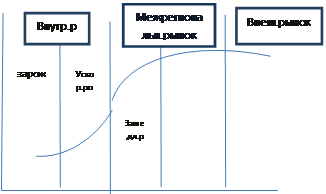
График жизненного спроса на продукцию
Чтобы заниматься прогнозированием, нужно найти функциональную зависимость, которая выражается динамичными функциями распределения, построенными на основе аппроксимации исходных данных по объему продаж. Задача выбора характера распределения объемов продаж конкретного продукта компании является одной из ключевых при моделировании динамического ряда. Для продукта, уже реализуемого на рынке, характер распределения объема продаж можно установить путем экстраполяции сложившейся тенденции. Для этого подходит визуальный метод, в основе которого лежит графическое представление этого распределения.
Для прогнозирования спроса исходя из графического представления его распределения можно использовать различные функции:
1) логистическая функция вида: E(t)=E*/1+e^-at
где а>0, Е* - максимальное значение объема спроса или продаж в динамическом ряду;
2)E(t)=A/1+10^a+bt или E(t)=A/1+10^a+bt + C
где а, в>0 – параметры. А – разница между первым и последним значением спроса в динамическом ряду объемов спроса, С – первое значение в динамическом ряду;
3) функция Гомперца: E(t)=Е*умножить a^b^t
Для того чтобы осуществить окончательный выбор функции нужно на плоскость нанести точки динамического ряда объемов спроса, а потом соединить их кривой и посмотреть, что она из себя представляет. Нужно открыть справочник по высшей математике и найти график, соответствующий этой функции. Найти функцию, найти коэффициенты.
Методика и компьютерная реализация этой задачи:
6. Построим таблицу объемов спроса на нашу продукцию
| Динамический ряд объемов спроса на продукцию предприятия | |||||
| Показатель | Годы | ||||
| Объемы спроса на продукцию, млн. руб. | 1,14 | 1,9 | 4,7 | 8,7 | 9,2 |
7. Выделим диапазон ячеек и по ним построим график. Эта кривая напоминает логистическую функцию следующего вида y=A/1+10^a+bx:
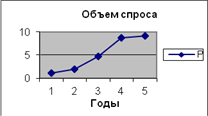Для того, чтобы её можно было использовать для прогнозирования спроса на следующем промежутке времени нужно найти А, а, b.
8. Затем подставим года и проверим будут ли большие расхождения между практическими и теоретическими значениями и определим можно ли использовать ей для дальнейшего прогнозирования.
9. Годы нумеруются от 1 до 5
10. 1+10^a+bx=А/у; 10^a+bx= А/у-1; a+bx=lg(А/у-1)
Затем найдем коэ-ты a и b =ЛИНЕЙН(диапазон у; диапазон х)
Реализация методики: создаём первую таблицу и называем ее «Объемы спроса на продукцию»(см. таблица выше). И по данным этой таблицы строим график(выше), затем переходим и формируем табл. 2 она называется «Данные и формулы для вычисления коэффициентов а и b» Таблица имеет следующий вид:
| Определение коэффициентов a и b логистической функции | ||||||
| X | Y0 | A/Y - 1 | Lg(A/Y - 1) | Коэффициенты | ||
| 1,14 | С10 | D10 | ||||
| 1,9 | b | a | ||||
| 4,7 | -0,446762 | 1,9528456 | ||||
| 8,7 | ||||||
| 9,2 |
С10= ($F$5-$B$5)/(B10-1) и вниз
D10= LOG(C10;10) и вниз
После этого выделяем диапазон F9:G9 и формулу = ЛИНЕЙН(D10:D14;A10:A14) Ctrl+Shift+Enter. Появятся коэффициенты.
Формируем таблицу 3.
| Теоретические и прогнозируемые объемы спроса на продукцию | ||||
| X | k=a+b*x | 10^k + 1 | Y1=A/(1+10^k) | (Y1-Y0)^2 |
| В19 | С19 | D19 | Е19 | |
В19= $G$12+$F$12*A19 и копируем вниз
С19= СТЕПЕНЬ(10;B19)+1 и вниз
D19= ($F$5-$B$5)/C19 и вниз
Е19= (D19-B10)^2 и копируем вниз 5 раз
После этого строим график по столбцу В. Если графики построенные по теоретическим и по практическим значениям объемов спроса хорошо согласуются между собой, то полученное значение E1(t) можно использовать для прогнозирования спроса на следующее время.
Если прогнозирование спроса осуществить на основе функции Гомперца, то для определения параметров а и b этой функции нужно прологарифмировать обе части функции Гомперца по основанию ½. То есть используем полученное уравнение вида:
y=a^b^x
log1/2(E(t)/E*)=log1/2 a^b^x=b^t*log1/2 a
Для определения параметров уравнения а и b есть функция = ЛГРФПРИБЛ (диапазон у; диапазон х)
Вывод: таким образом, согласно проведённым расчетам, логистическая функция более адекватная реальной тенденции продаж и поэтому прогноз следует строить по модели E(t)=A/1+10^a+bt.
