Приемы обработки Р.Д. (укрупнение интервалов, сглаживание методом скользящей средней)

При анализе рядов динамики возникает необходимость выявления общей тенденции развития (тренда), исключая разного рода отклонения, вызванные разными факторами. Для этого используют следующие методы: 1.Укрупнение интервалов. 2. Сглаживание скользящей средней. 3.Аналитическое выравнивание.

Метод скольз. средней. в нем при помощи исх. данных опр-ют сглаж. ряд, в кот отчетливо прослеж. тенденция динамики в виде плавн. линии.

Расчет скользящей средней производится следующим образом:

1.Среднегод-я берется как среднеарифм-я.

2.убирается 1-й уровень и добав-ся след-й уровень. Для нечет числа уровней каждое знач сколь-е ср. приходится на промежуток м/у 2-мя смежными кварталами. Если чет число, то будет произ-ся центрирование.

3 Центрирование берется как средняя арифме-я простая м/у смежными уровнями

Метод укрупненного интервала –выявляется для опред-я тренда в Р.Д. колеблющихся уровней затушевывающих основную тенденцию развития. Главное в нем преобразование первоначального Р.Д. в ряд более продолжит-х периодов.

Аналитическое выравнивание Р.Д. Типы развития и соответствую-е им уровнения функций.

Задача аналитического выравнивания – найти плавную линию развития (тренд), характеризующую основную тенденцию динамики. Решение данной задачи начинается с подбора матем. функции, по которой рассчитываются теоретические уровни тренда. Для анализа используют следующие формулы:

Равномерное развитие

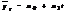- уравнение прямой, где 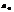и 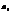- параметры уравнения; t – обозначение времени

2.Равноуско-ое , равнозамедл-е разв-едля него хар-ы постоян-е темпы прироста Если а2 >0-ускорен-е a2<0-равнозамедл-е

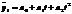- уравнение параболы 2 порядка.

Развитие с перемен-м ускорен-м, замедлен-ем

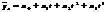-уравнение параболы 3 порядка.

Развитие по экспоненте хар-но постоян-е темпы роста

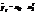- показательная функция.

Развит-е с замедле-ем роста

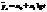- полулогарифмическая функция.

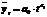- степенная функция.

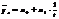- гиперболическая функция.

Для опред-я какая модель явл-ся наиб-ее адекватной сравнив-ся их стандартизированные ошибки

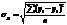, дописать над у черточку,чем меньше 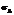, тем адекватнее математическая функция.

Синтезирование трендовой модели на основе уравнения прямой. Показатели адекватности математич-ой функции в р.д.

Аналит. выр-ние: с-ма 2х лин. Ур-ний для опр-ния пар-ров а₀ и а₁

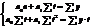
При использовании способа условного обозначения времени (отсчёта времени от условного начала) 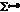, тогда

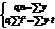, отсюда параметры: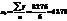

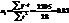
По вычисленным параметрам производим синтезирование трендовой модели:

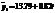, затем для каждого года анализируемого ряда динамики по синтезируемой модели определяются теоретические уровни тренда. В качестве показателя адекватности математической функции используют стандартизированную ошибку аппроксимации:

,

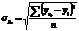чем меньше 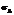, тем адекватнее мат. функция.