Методы уменьшения риска финансовых операций

Диверсификация

Данный метод уменьшения рисков заключается в распределении временно свободных финансовых средств по нескольким не зависимым друг от друга финансовым операциям. Предположим, что некоторая сумма средств 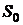распределяется по n независимым друг от друга финансовым операциям:

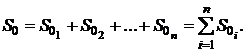
По завершении финансовых операций полученная сумма финансовых средств будет равна:

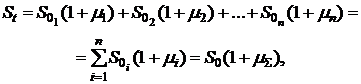(3.16)

где 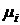- доходность по i-й финансовой операции (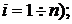

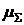- суммарная доходность по всем финансовым операциям.

Формулу (3.16) можно преобразовать к виду:

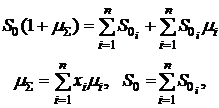(3.17)

где 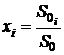- стоимостная доля средств, вложенных в i-ю финансовую операцию .

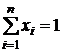Как отмечалось в п. 3.1 и 3.2, в реальных условиях доходности по каждой финансовой операции являются случайными, а значит, и суммарная доходность также будет случайной величиной. Оценку рисков данных финансовых операций будем осуществлять по коэффициенту вариации доходности:

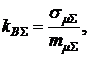
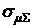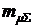где и - соответственно среднеквадратическое отклонение суммарной доходности и математическое ожидание суммарной доходности.

Если i-е финансовые операции являются независимыми, то для 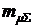и 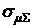можно с учетом формулы (3.17) записать следующие равенства:

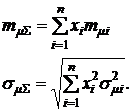(3.18)

Коэффициент вариации по данным финансовым операциям определится отношением

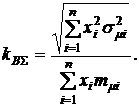(3.19)

При одинаковых значениях средних доходностей по всем финансовым операциям 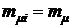формула (3.19) упрощается и может быть в виде:

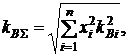(3.20)

где 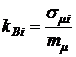- коэффициент вариации по каждой i-й финансовой операции.

При n = 2 значения долей финансирования х₁ и х₂, обеспечивающие минимальное значение 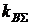(минимальные риски), можно вычислить по формулам: 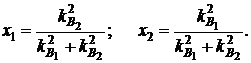(3.21)

При этих значениях х₁ и х₂ минимальное значение коэффициента вариации будет равно 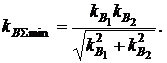(3.22)

Из формулы (3.21) видно, что оптимальные доли финансовых средств х₁ и х₂, обеспечивающие 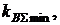определяются равенством:

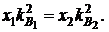
Из рис. 3.2 и формулы (3.22) видно, что коэффициент вариации суммарной доходности по двум независимым финансовым операциям будет меньше, чем наименьшее значение коэффициента вариации из используемых двух операций.

При 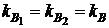минимальное значение 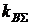(минимальные риски) обеспечивается при 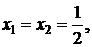а минимальное значение коэффициента вариации равно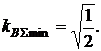

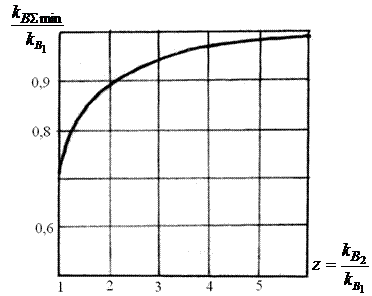
Рис. 3.2. Зависимость минимального значения суммарного коэффициента вариации от соотношения коэффициентов вариации по двум финансовым операциям

Можно также показать, что при одинаковых рисках каждой i-й финансовой операции ( ) минимальное значение коэффициента вариации по всем i-м операциям 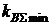обеспечивается при равных стоимостных долях средств, вложенных в каждую финансовую операцию 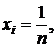и, как видно из выражения (3.22), будет равно:

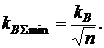
Из данной формулы видно, что отношение риска 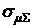суммарной финансовой операции, состоящей из "n" независимых финансовых операций, к ее среднему доходу 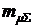при одинаковых коэффициентах вариации по каждой i-й финансовой операции ( 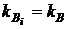) может быть в 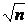раз меньше финансового риска каждой i-й финансовой операции. Этот эффект называется эффектом диверсификации. Данный принцип распределения инвестиционных средств известен как принцип "не класть все яйца в одну корзину".

Следует отметить, что метод диверсификации дает эффект только при распределении инвестируемых средств в независимые друг от друга финансовые операции, когда случайные доходности по i-м финансовым операциям, по крайней мере, не коррелированны.

Хеджирование

Суть хеджирования состоит в подборе к основной финансовой операции таких дополнительных финансовых операций, которые при их совместном проведении уменьшают риск. При хеджировании не накладывается ограничение на независимость финансовых операций. Если основная и дополнительная финансовые операции являются коррелированными (зависимыми), то для среднеквадратического отклонения суммарной доходности этих двух операций можно записать:

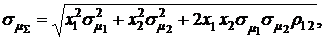(3.23)

где 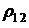- коэффициент корреляции доходностей основной 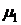и дополнительных финансовых операций, определяющийся по формуле:

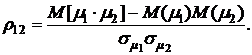
Значения коэффициента взаимной корреляции могут находиться в пределах 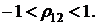При 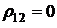основная и дополнительная операции не коррелированны (независимы). При увеличении рисков по одной финансовой операции риски по другой операции также увеличиваются, если 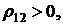а если 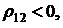то риски по второй финансовой операции имеют тенденцию к снижению.

Дифференцируя формулу (3.23) по х₁ с учетом х₂ = 1 – х₁ и приравнивая производную к нулю, получим, что оптимальные значения х₁ и х₂, обеспечивающие минимальное значение 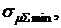определяются формулами:

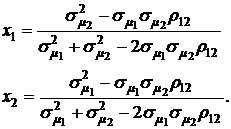(3.24)

Математическое ожидание суммарной доходности основной и дополнительной финансовой операции при соблюдении неравенств 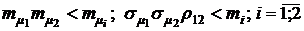определится формулой:

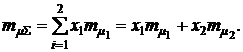
При одинаковых значениях средних доходностей 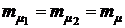для суммарной доходности получим 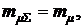а для коэффициента вариации суммарной доходности с учетом формулы (3.23) получим:

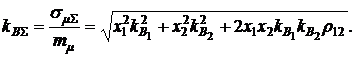(3.25)

Из формулы (3.25) видно, что при 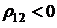коэффициент вариации (риск) суммарной финансовой операции уменьшается при уменьшении 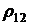до -1.

Дифференцируя формулу (3.24) по х₁ с учетом 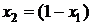и приравнивая производную нулю, получим, что оптимальные значения долей основной х₁ и дополнительной х₂ финансовых операций, обеспечивающие минимальное значение суммарного риска 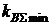при хеджировании, можно вычислить по формулам:

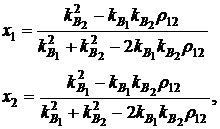(3.26)

при *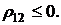

Формулы (3.24) и (3.26) дают одинаковые значения оптимальных долей финансирования, так как при 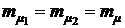, поделив числитель и знаменатель в формуле (3.24) на 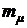, мы получим формулы (3.26).

Оптимальные значения стоимостных долей финансовых операций при различных значениях средних доходностей 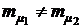будут получены в п. 4.3.

Из формул (3.26) видно, что при 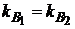оптимальные значения долей основной и дополнительной финансовых операций одинаковы: 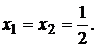На рис. 3.3 приведены зависимости оптимальных значени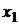й и 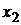от отношения 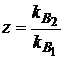при различных значениях коэффициента корреляции 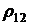основной и дополнительной финансовой операции. Из графиков рис. 3.3 следует, что при 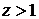( 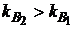) стоимостная доля основной операции х₁ должна быть больше 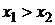, так как риски по этой финансовой операции меньше ( 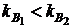). С уменьшением коэффициента корреляции 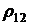от 0 до -1 разница между стоимостными долями финансовых операций незначительно уменьшается.

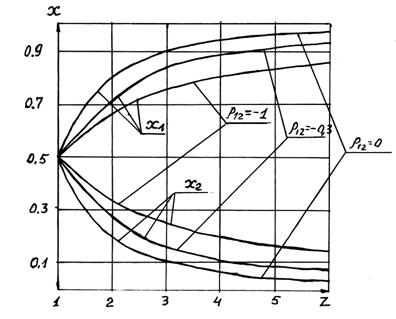
Рис. 3.3. Зависимость оптимальных значений стоимостных долей финансовых операций от соотношения коэффициентов вариаций

После подстановки формул (3.26) в (3.25) для минимального значения коэффициента вариации суммарной доходности при хеджировании получим:

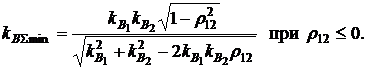(3.27)

На рис. 3.4 приведены графики 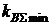от коэффициента корреляции основной финансовой операции 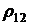при двух значениях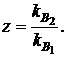

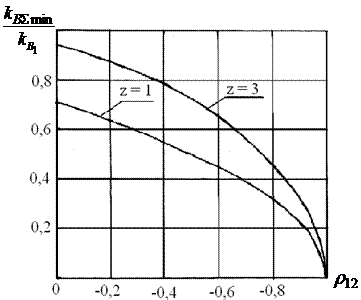
Рис. 3.4. Зависимость минимального значения суммарного коэффициента вариации от коэффициента корреляции доходностей финансовых операций

Из приведенных графиков видно, что для уменьшения коэффициента вариации (риска) суммарной финансовой операции при хеджировании нужно подбирать дополнительную финансовую операцию примерно с такими же рисками, как и по основной 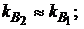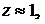и коэффициент взаимной корреляции рисков основной и дополнительной финансовой операции должен быть отрицательным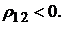

На практике не всегда бывает просто подобрать дополнительную финансовую операцию при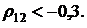

Разновидностями хеджирования являются такие финансовые операции, как опционы и страхование.

Опционы – это вид биржевой сделки с премией, уплачиваемой за право продать или купить финансовый актив в определенном количестве по цене и в сроки, оговоренные в опционном контракте.

Страхование – это финансовая операция, направленная на компенсацию (в денежной форме) возможных убытков при наступлении страхового случая.