Тесты для проверки качества усвоения пройденного материала
16. Формула сложных процентов:
A – FV = PV(1 + n*r)
B – FV = PV(1 + t / T * r)
C – FV = PV(1 + r) n
D – FV = PV(1 + n*r)*(1 + r)n
17. Начисление по схеме сложных процентов предпочтительнее:
A – при краткосрочных финансовых операциях;
B – при сроке финансовой операции в один год;
C – при долгосрочных финансовых операциях;
D – во всех вышеперечисленных случаях.
18. Чем больше периодов начисления процентов:
A – тем медленнее идет процесс наращения;
B – тем быстрее идет процесс наращения;
C – процесс наращения не изменяется;
D – процесс наращения предсказать нельзя.
19. Номинальная ставка – это:
A – годовая ставка процентов, исходя из которой определяется величина ставки процентов в каждом периоде начисления, при начислении сложных процентов несколько раз в год;
B – отношение суммы процентов, выплачиваемых за фиксированный отрезок времени, к величине ссуды;
C – процентная ставка, применяется для декурсивных процентов;
D – годовая ставка, с указанием периода начисления процентов.
20. Формула сложных процентов с неоднократным начислением процентов в течение года:
A – FV = PV(1 + r) m * n
B – FV = PV(1 + r / m) m*n
C – FV = PV / m * (1 + r) n / m
D – FV = PV(1 + r * m) m* n
21. Эффективная ставка процентов:
A – не отражает эффективности финансовой операции;
B – измеряет реальный относительный доход;
C – отражает эффект финансовой операции;
D – зависит от количества начислений и величины первоначальной суммы.
22. Формула сложных процентов с использованием переменных процентных ставок:
A – FV = PV(1 + r1) n1 * (1 + r2) n2 *… *(1 + rk) nk
B – FV = PV(1 + nkrk)
С – FV = PV(1 + n1r1 * n2r2 *… *nkrk) nk
D – FV = PV(1 + r*n)*(1 + r)
23. В случае, когда срок финансовой операции выражен дробным числом лет, начисление процентов возможно с использованием:
A – общего метода;
B – эффективной процентной ставки;
C – смешанного метода;
D – переменных процентных ставок.
24. Смешанный метод расчета:
A – FV = PV(1 + r)а + в
B – FV = PV(1 + r)а *(1 + вr)
C – FV = PV(1 + а*в*r)n
D – FV = PV(1 + r)а *(1 + r)в
25. Непрерывное начисление процентов – это:
A – начисление процентов ежедневно;
B – начисление процентов ежечасно;
C – начисление процентов ежеминутно;
D – начисление процентов за нефиксированный промежуток времени.
26. Если в условиях финансовой операции отсутствует ставка сложных процентов, то:
A – ее определить нельзя;
B –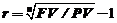 
C – r= ln(FV / PV) / ln(1 + n)
D – r= lim(1 + r / m)m
E – r=(1+r\m)m-1
2.3.7. Задачи для самостоятельного решения
Для выполнения заданий создавайте таблицы, подобные приведенной на рисунке (правая таблица дана в режиме отображения формул)
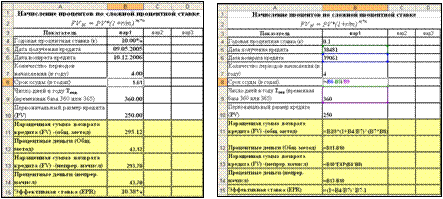
ðВ ячейках А3:А15 размещаются наименования показателей финансовой операции (наименования показателей могут изменяться в зависимости от постановки задачи);
ðв ячейках В4:В7 и В9:В10 размещаются исходные данные;
ðв ячейке В8 рассчитывается срок кредита =B6-B5, (если он не задан конкретно);
ðв ячейках В11:В15 записываются формулы вычисления наращенной суммы ( в зависимости от метода расчета ); процентных денег и эффективной процентной ставки (=B10*(1+B4/B7)^(B7*B8), =B11-B10, =B10*EXP(B4*B8), =B13-B10 и =(1+B4/B7)^B7-1, соответственно)
Примечание:
В ячейках столбцов C и D размещаются исходные данные и результаты решения задачи при различных значениях (вариантах) исходных данных.
Задание 1‑12
1. Ссуда в размере 50000 руб. выдана на полгода по сложной ставке 18% годовых. Определить наращенную сумму и сумму начисленных процентов.
Ответ: FV= 57000; I= 7000 (руб.)
Задание 1‑13
Рассчитать какая сумма окажется на счете, если 27 тыс. руб. положены на 33 года под 13.5% годовых. Проценты начисляются каждые полгода.
Ответ: 2 012 074.64р
Задание 1‑14
По вкладу в 10000,00, помещенному в банк под 5% годовых, начисляемых ежегодно, была выплачена сумма 12762,82.
а) Определить срок проведения операции (количество периодов начисления).
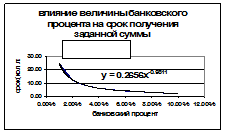б) используя построение сценария (или таблицу подстановки), выясните, как влияет банковский процент (в диапазоне от 1% до 10 %) на срок получения указанной суммы. Постройте диаграмму, отражающую эту зависимость.
Ответ: а) 5 лет
Задание 1‑15
Сумма в 10000 помещена в банк на депозит сроком на 4 года. Ставка по депозиту – 10% годовых. Проценты по депозиту начисляются раз в год. а)Какова будет величина депозита в конце срока?
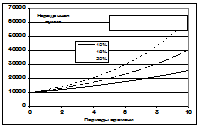б) На какой срок должны быть положены деньги на депозит, с тем, чтобы к концу срока накопленная сумма составила 20000 руб.
в) Постройте диаграмму, иллюстрирующую зависимость величины наращенной суммы от периода времени наращения
Ответ:
а) 14 641.00р.
б) 7.27 года
Задание 1‑16
Был сделан заем в 1000 тыс. руб. с номинальной процентной ставкой 12% и сроком уплаты 3 года. Какая сумма будет выплачена кредитору в конце срока, если начисление процентов: полугодовое, квартальное, ежемесячное, ежедневное.
Ответ:
а) 1418.53; b) 1425.76; c) 1430.77; d) 1433.24
Задание 1‑17
Вкладчик, решивший положить на депозит 250 тыс. руб., хочет накопить через год не менее 400 тыс. руб. Определить ставку процентов, на основании которой он может выбрать подходящий для этой цели банк. Начисление процентов банков производится непрерывно.
Ответ: r=47%
Задание 1‑18
Определить процентную ставку, которую использует банк для вкладов до востребования, если при первоначальной сумме вклада 1000 руб. через 6 месяцев начислено 1084 руб.
Ответ: r = 16,24%
Задание 1‑19
Вкладчик собирается положить в банк 500 тыс. руб., чтобы накопить 700 тыс.руб. Ставка процентов банка составляет 15% годовых. Проценты начисляются ежемесячно.
Определите срок в днях, за который вкладчик сможет накопить требуемую сумму (число дней в году равно 360).
Ответ: t = 2,26 года = 812,56дн.
Дисконтирование
В практике финансовых расчетов часто приходится решать задачи, обратные определению наращенной суммы: по уже известной наращенной сумме (FV) следует определить неизвестную первоначальную сумму долга (PV).
Наиболее часто такие ситуации возникают при разработке условий финансовой сделки, когда проценты с наращенной суммы удерживаются непосредственно при выдаче ссуды. Процесс начисления и удержания процентов вперед, до наступления срока погашения долга, называют учетом[12], а сами проценты в виде разности наращенной и первоначальной сумм долга дисконтом (discount).
Именно дисконтирование позволяет учитывать в стоимостных расчетах фактор времени, поскольку дает сегодняшнюю оценку суммы, которая будет получена в будущем. Привести стоимость денег можно к любому моменту времени, а не обязательно к началу финансовой операции.
Различают математическое дисконтирование и коммерческий (банковский) учет.