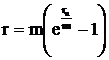Начисление процентов несколько раз в год
Сложный процент может начисляться чаще, чем один раз в год, например, раз в полгода, квартал, месяц и т.д. В этом случае формула принимает вид:
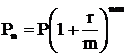
где: m – периодичность начисления процента в течение года.
Непрерывное начисление процента
Сложный процент может начисляться очень часто. Если периодичность начисления процентов стремиться к бесконечности (m→∞), то мы получим непрерывное начисление процентов. Несмотря на то, что логически непросто представить себе частоту начисления процентов, равную бесконечности, математически возможно определить ту сумму средств, которую получит инвестор, если разместит деньги на условиях непрерывно начисляемого процента. Формула для непрерывно начисляемого процента имеет следующий вид:
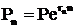
где: rn – непрерывно начисляемый процент;
n – период времени начисления процента;
е = 2,71828...
Эту формулу можно получить следующим образом:
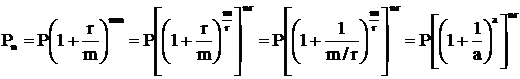
где:
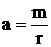
При непрерывном начислении процентов m→∞ и, следовательно, a→∞. В этом случае:
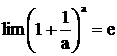
m→∞
Тогда
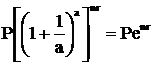
Эквивалентный и эффективный проценты
В практике финансового рынка процент, начисляемый по активу, задают как простой процент в расчете на год. Однако если в рамках года по активу предусмотрено начисление сложного процента, то общий результат, который получит инвестор, будет выше декларируемого. Чтобы его определить необходимо рассчитать эффективный или реальный процент.
Эффективный (реальный) процент – это процент, который получается по итогам года при начислении сложного процента в рамках года.
Эффективный процент можно определить из следующего соотношения:
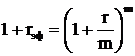
где: rэф – эффективный процент,
r – простой процент в расчете на год, который задан по условиям финансового инструмента.
Тогда:
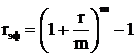
Если известен эффективный процент, то по формуле, которая вытекает из формулы (11), можно определить эквивалентный ему простой процент в расчете на год:
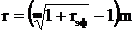
Эквивалентность непрерывно начисляемого процента и процента, начисляемого m раз в год
В финансовых расчетах может возникнуть необходимость найти эквивалентность между непрерывно начисляемым процентом и процентом, начисляемым т раз в год. Например, в формулах определения курсовой стоимости опциона используется непрерывно начисляемый процент. В то же время на финансовом рынке инвесторы оперируют главным образом ставками, предполагающими начисление процента раз в год, полгода, квартал и месяц.
Эквивалентность между двумя видами процентов можно найти, приравняв суммы, получаемые с учетом непрерывно начисляемого процента и начисления процента т раз в год, а именно:
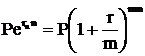 ,
,
где: rn– непрерывно начисляемый процент
или
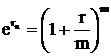
Отсюда
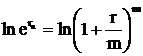
или
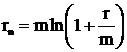
Процент r можно получить следующим образом: