Концепция временной стоимости денег

Деньги (англ. money, нем. geld) – универсальное средство обмена, особый товар, наделенный свойством всеобщего эквивалента, посредством которого выражается стоимость всех других товаров.

Временная стоимость денег – это стоимость денег с учётом фактора времени.Стоимость денег – непостоянная, изменчивая величина, подверженная влиянию мно­жества факторов, но основной фактор влияния – время. Деньги как особый вид товара обладают свойством терять свою ценность по мере их отдаления от сегодняшнего момента времени, а также от времени их активного исполь­зования. Стоимость денег сегодня намного больше, чем бу­дет завтра или в отдаленном будущем. Это «золотое» правило базируется на той истине, что де­нежные средства, которыми можно распоряжаться сегодня, должны быть немедленно направлены на конкретное дело – развитие производства, покупку ценных бумаг, депозиты в банках. Тем самым они способны заработать новые деньги, принести дополнительные доходы. Отсрочка «деятельности денег» означает временное их бездействие, что приносит потери от нереализованных возможностей. Многолетний опыт деятельности хозяйствующих субъектов разных стран подтверждает аксиому, что чем длиннее процесс «замора­живания» денег, тем весомее становятся потери от недопо­лученных доходов.

Концепция временной стоимости денег сводится к следующему:некоторая сумма денежных средств сегодня дороже, чем та же сумма завтра, так как:

а) располагая денежными средствами «сегодня», экономический субъект может вложить их в какое-нибудь доходное дело и заработать прибыль, в то время как получатель будущих денег лишен этой возможности. Возможность наращивать сегодняшние деньги, размещая их в доходные операции, делает их более ценными, чем те деньги, которые мы получим в будущем.

б) инфляционные процессы снижают реальную покупательную способность денег. В условиях инфляции на определенную сумму денежных средств сегодня можно приобрести большее количество товаров, работ и услуг, чем на ту же сумму в будущем. Поэтому «сегодняшние» деньги ценнее «завтрашних».

в) «сегодняшние» деньги всегда будут ценнее «завтрашних» также из-за риска неполучения последних, и этот риск будет тем выше, чем больше промежуток времени, отделяющий получателя денег от этого «завтра».

В связи с изменчивой стоимостью денег многие текущие затраты, вложения неправомерно сравни­вать с будущими денежными поступлениями. В таких случаях предполагаемый эффект не отражает реальной доходности.

Поэтому все принимаемые экономические реше­ния должны учитывать фактор времени. С точки зрения временной стоимости денег некорректно суммировать или вычитать денежные величины, относящиеся к разным периодам времени без приведения их к единому моменту времени (сегодняшнему, или к какому-либо моменту в будущем). Для приведения денежных величин к единому моменту времени используют следующие операции:

1. Операция наращения (капитализации), то есть определения будущей стоимости “сегодняшних” денег. Будущую стоимость денег при этом называют наращенной.

Будущая стоимость денежных средств определяется по формуле

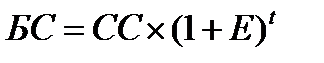, (2.3)

где БС – будущая стоимость, руб.; СС – сегодняшняя стоимость, руб.;

Е – норма дисконта, в долях от единицы; t – количество периодов расчета.

Определение стоимости денег и ее изменение во времени осуществляется при помощи цены денег, которая также явля­ется динамичной. Цена денег появляется только на финансовом рынке в виде платы за временное использова­ние чужого капитала, и в отличие от стоимости денег, определяемой в стоимостных единицах, выражается в процентах годовых. В формулах 2.3 и 2.4 в качестве нормы дисконта чаще всего используется цена денег.

Пример 2.1. Вложения капитала в бизнес (в активы) составляют $ 10 тыс. Ожидаемая чистая доходность активов – 20 % годовых. Определить в системе капитализации объем активов через 3 и через 10 лет при неизменной доходности и при условии 100 %-ого реинвестирования прибыли. (Реинвестирование прибыли – это вложение прибыли в тот же бизнес, который ее аккумулировал).

Решение:

К концу первого года предприятие получит прибыль в размере:

10 000 × 0,2 = $ 2000.

Общий объем активов при условии 100 %-ого реинвестирования прибыли составит:

10 000 + 2000 = 10 000 (1 + 0,2) = $ 12000.

К концу второго года объем активов составит:

12 000 (1+ 0,2) = 10 000 (1+ 0,2) 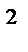= $14400.

К концу третьего года:

14 400 (1+ 0,2) = 10 000 (1+ 0,2) 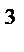= $ 17280.

К концу десятого года объем активов составит:

10 000 (1+ 0,2) 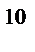= $ 61917.

По аналогии можно рассчитать сумму денежных средств, которую вкладчик получит по депозиту при капитализации процентов, если его первоначальный вклад составит $ 10000, процентная ставка по депозиту 20 % годовых, срок договора – 3 года, 10 лет.

Обозначим доходность активов в размере 0,2 через Е. Тогда 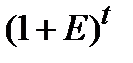– множитель капитализации.

Если норма дисконта (доходность) меняется по годам, то формула 2.3 будет иметь следующий вид:

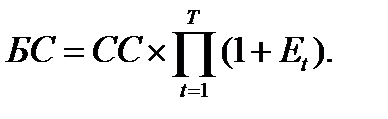(2.4)

2. Дисконтирование – операция, обратная капитализации, то есть дисконтирование – это приведения будущей стоимости к сегодняшнему моменту времени, то есть определение сегодняшней стоимости «завтрашних» денег. Сегодняшнюю стоимость денег при этом называют современной, текущей или приведенной стоимостью. Дисконтирование используют, например, для определения современной стоимости денег, которыми собираются рассчитаться через год после поставки товара.

Различают два вида дисконтирования: математическое дисконтирование (см. пример 1) и дисконтирование по методу банковского учета.

1. Математическое дисконтирование, при котором определяется сегодняшняя стоимость будущих денег, осуществляется по формуле

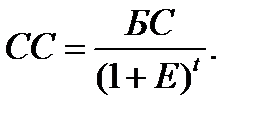(2.5)

Как можно заметить, формулу 2.5 получили «математически», выражая СС (сегодняшнюю стоимость) из формулы 2.3.

При изменяющейся по периодам доходности формула 2.5 будет иметь вид:

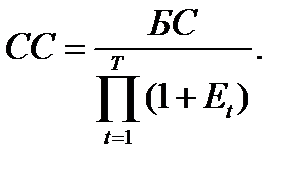(2.6)

Пример 2.2. Предприятие обязуется поставить товар через 120 дней в сумме 3 млн. руб. Определить современную (текущую) стоимость товара при норме дисконта 10 %.

Решение:

1. Текущая стоимость товара при использовании метода математического дисконтирования

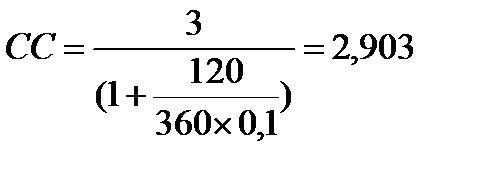млн. руб.

2. Текущая стоимость товара при использовании метода банковского учета

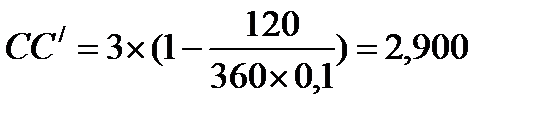млн. руб.

Вывод: для поставщика более «выгодным» оказывается второй вариант, так его доход в этом случае больше.

2. Банковский учет. Этот вид дисконтирования получил широкое распространение при определении размера выкупной цены простого или переводного векселя при его учете в коммерческом банке, когда банк выкупает у владельца вексель до истечения обозначенного на нем срока погашения по цене ниже номинала. В этом случае сумма денежных средств, обозначенная в векселе (номинал), представляет собой «будущие деньги», выкупная цена представляет собой «сегодняшние деньги». При расчете дисконта как разницы между номиналом и выкупной ценой векселя определяют сегодняшнюю стоимость будущих денег, то есть проводят дисконтирование по методу банковского учета. Ставка дисконта при этом называется учетной ставкой и является сложной.

Пример 2.3. Владелец векселя номиналом 25 тыс. руб. обратился в банк с предложением учесть его за год до наступления срока погашения. Банк согласен выполнить эту операцию по учетной ставке 15 % годовых. Рассчитать сегодняшнюю стоимость векселя, то есть его выкупную цену.

Решение:

1. Дисконт = 25 000 × 0,15 = 3 750 тыс. руб.

2. Сегодняшняя стоимость векселя (за вычетом дисконта) = 25 000 – 25 000 × 0,15 = 25 000 × (1 – 0,15) = 21 250 руб.

Обозначим учетную ставку через Е и получим 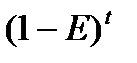– множитель дисконтирования по методу банковского учета. Тогда определение сегодняшней стоимости будущих денег по методу банковского учета будет осуществляться по формуле

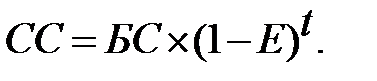(2.7)

При проведении финансовых расчетов в случае использования математического дисконтирования и банковского учета результаты расчетов будут разными. Но при принятии финансовых решений (сравнении двух и более вариантов действий) выбор метода расчета (капитализация, математическое дисконтирование или банковский учет) не оказывает влияния на выбор. Если один из вариантов оказывается более предпочтительным при использовании капитализации, то он будет более выгодным по сравнению с другими вариантами и при расчете в системе математического дисконтирования и в системе дисконтирования по методу банковского учета. Поэтому выбор метода расчета – это чаще всего вопрос целесообразности и удобства в проведении расчетов. Например, если вы решили приобрести какой-либо товар и его сегодняшняя стоимость известна, а для его покупки вы собираетесь копить деньги из заработной платы, то, очевидно, что расчеты удобнее вести в системе математического дисконтирования. При этом стоимость самого товара пересчитывать в системе дисконтирования не надо, так как его стоимость уже определена в «сегодняшних» деньгах. Дисконтирование надо будет применить только к поступлениям денежных средств в виде будущей заработной платы, и после этого можно будет рассчитать, через какое время вы сможете совершить покупку.

Выбор между математическим дисконтированием и банковским учетом имеет значение только при определении цены на финансовые активы, например, при заключении фьючерсных или форвардных контрактов, определении возможной реализационной стоимости облигаций и других финансовых активов.

Таким образом, при принятии финансовых решений, связанных с выбором одного из множества альтернативных вариантов действий, необходимо анализировать скорректированные денежные потоки, генерируемые каждым из этих вариантов, на единый для всех вариантов момент времени, что дает возможность провести их корректное сравнение.

В формулы 2.3 – 2.7 может быть введена инфляция, которая выступает одним из факторов обесценивания денег, а, следовательно, влияет на их временную стоимость.

Введем следующие понятия:

1. Номинальная процентная ставка – ставка, не включающая премию за инфляцию, то есть ставка при безинфляционной экономике. Эту ставку в формулах 2.3 – 2.7 мы обозначали через Е.

2. Реальная процентная ставка – номинальная ставка, откорректированная с учетом инфляции.

Пример 2.4. Банк располагает свободной суммой денежных средств в размере 100 млн. руб. Номинальная процентная ставка составляет 5 %. Известно, что цены за год вырастут на 10 %.

Решение.

Следовательно, чтобы «не потерять деньги» в связи с инфляцией банк, согласится «расстаться» на год с суммой в 100 млн. руб., если получит через год сумму, не меньшую 100 × (1+0,10) = 110 млн. руб., но в этом случае он лишь вернет себе деньги, ничего не заработав. Для того, чтобы заработать свои 5 %, он должен получить через год:

110 000 × 1,05 =100 × (1 + 0,10) × (1 + 0,05) = 100 × (1 + 0,10 + 0,05 +

+ 0,10 × 0,05) = 100 × (1 + 0,155) = 115, 5 млн. руб.

Следовательно, реальная процентная ставка составит 15,5 % или

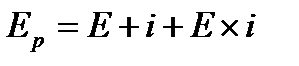, (2.8)

где 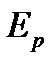– реальная процентная ставка, в долях от единицы; Е – номинальная процентная ставка, в долях от единицы; i – ожидаемый темп инфляции, в долях от единицы.

Выводы, сделанные на основе применения концепции временной стоимости денег:

- некорректность (с точки зрения анализа долгосрочных финансовых операций) суммирования (вычитания) денежных величин, относящихся к разным периодам времени без приведения их к единому моменту времени;

- чем дольше процесс «замораживания» денег, тем больше недополученные доходы (упущенная выгода);

- в качестве нормы дисконта (капитализации) в зависимости от вида операции (сделки), финансового инструмента могут использоваться:

- средневзвешенная цена капитала;

- ставка по депозитам;

- чистая рентабельность активов предприятия;

- ставка рефинансирования;

- фондорентабельность и т. п.

Что именно будет использоваться в качестве нормы дисконта (нормы капитализации), зависит от конкретной задачи и особенностей функционирования организации.