Реальная производительность (производительность на тестах)

Существующие тестовые наборы можно разделить на три группы:

· тесты производителей (компаний-изготовителей компьютеров), предназначенные, как правило, для сравнения однотипных компьютеров, относящихся к одному семейству;

· стандартные тесты, разработанные независимыми аналитиками и предназначенные для сравнения широкого спектра компьютеров;

· пользовательские тесты, учитывающие специфику решаемых пользовательских задач.

В вычислительной практике чаще всего применяют стандартные тесты. Рассмотрим некоторые из них.

Поскольку большую часть времени выполнения программ обычно занимают циклы, часто именно они применяются в качестве тестов. В настоящее время наиболее известным тестом производительности является набор тестов Linpack, который представляет собой набор программ для решения СЛАУ методом исключения Гаусса. Основным параметром тестов Linpack является порядок СЛАУ 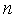. Обычно используются тесты с 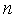=100 и тесты 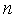=1000. Известно количество операций (как функция размерности СЛАУ 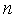), которые необходимо выполнить для решения систем линейных алгебраических уравнений (СЛАУ) методом исключения Гаусса. Поэтому, зная время решения задачи, легко найти производительность системы в MFLOPS. Известный список TOP 500, включающий в себя 500 самых высокопроизводительных компьютеров мира, строится на основе тестирования с помощью тестов Linpack.

Для MPP-систем часто используют набор тестов Linpack-parallel. Приведем результаты исполнения теста Linpack-parallel на некоторых параллельных системах:

· 6768-процессорный Intel Paragon - 281 GFLOPS при N = 128600;

· Cray T916 - 522 MFLOPS при N=100;

· Hitachi S3800 - 6431 MFLOPS при N=1000.

Для суперкомпьютеров широко используются набор тестов NAS parallel benchmark. Тесты представляют собой набор алгоритмов решения некоторых задач вычислительной газодинамики и гидродинамики.

Гипотеза Минского.

Гипотеза Минского. В 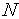-процессорной векторно-параллельной вычислительной системе или MIMD-вычислительной системе, в которой производительность каждого процессора равна единице, общая производительность 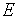растет как 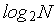(см. рис. 1)

В первых параллельных вычислительных системах, когда количество процессоров было невелико, гипотеза Минского подтверждалась. В современных системах с большим количеством процессоров имеет место зависимость производительности от числа процессоров, показанная на рис. 1 пунктиром. Основные причины такой зависимости:

· с ростом количества процессоров растут коммуникационные расходы (вследствие роста диаметра коммуникационной сети);

· с ростом количества процессоров растет несбалансированность их загрузки.

Таким образом, если количество процессоров системы 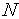превышает величину 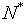, то целесообразно использовать мультипрограммный режим работы системы.

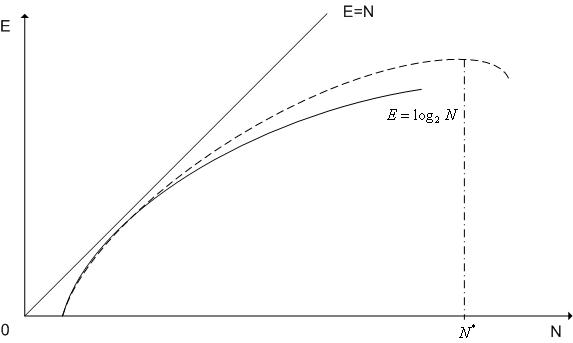Рис. 1. К гипотезе Минского.