Расчёт статически неопределимых систем методом сил в матричной форме

Система канонических уравнений метода сил (16.4) в матричной форме запишется:

dX + D_F = 0. (16.20)

d – матрица перемещений по направлению усилий в удалённых связях Х_i в единичных состояниях основной системы метода сил, или матрица внешней податливости основной системы метода сил по направлению X_i (i = 1, 2, …, n).

.

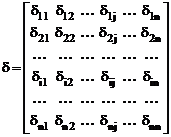Число строк и столбцов этой матрицы равно степени статической неопределимости сооружения n, т.е. матрица d – это квадратная матрица. С учётом теоремы о взаимности перемещений матрица d симметрична. В силу разрешимости системы уравнений (16.20) матрица внешней податливости основной системы метода сил является невырожденной, так как её определить не равен нулю (det d ¹ 0).

Х – матрица усилий в лишних связях сооружения, или матрица неизвестных метода сил.

.

D_F – матрица перемещений по направлению неизвестны метода сил в основной системе от заданного силового воздействия, или матрица свободных членов системы канонических уравнений метода сил.

.

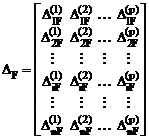Число строк в матрицах Х и D_F равно степени статической неопределимости сооружения n, а число столбцов – числу комбинаций внешних нагрузок р (постоянной и временных).

Элементы матриц d и D_F – это перемещения в основной системе метода сил по направлению усилий в удаленных связях X_i, соответственно, от единичных значений этих усилий и заданной нагрузки. Упомянутые перемещения d_ii, d_ij, D_iF можно вычислить в матричной форме, используя соотношение (13.18):

d = L^T B L, (16.21)

D_F = L^T B L_F. (16.22)

L – матрица необходимых для расчёта сооружения на силовое воздействие внутренних усилий (изгибающих моментов, поперечных и продольных сил) в основной системе метода сил от X₁ = 1, X₂ = 1, …, X_j = 1, …, X_n = 1.

L = [L₁ L₂ … L_j … L_n], .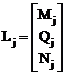

Число столбцов матрицы L равно числу неизвестных метода сил n, а число строк блоков M_j, Q_j, N_j этой матрицы определяется характером внешней нагрузки и числом грузовых участков сооружения.

Для k-го грузового участка с равномерно распределённой нагрузкой

.

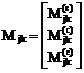Здесь в и е – концевые сечения грузового участка (начало и конец), с – среднее сечение грузового участка.

Для k-го грузового участка, на котором распределённой нагрузки нет

.

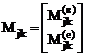Для участка с произвольно ориентированной по отношению к оси стержня равномерно распределённой нагрузкой

,

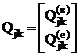для грузового участка с такой же нагрузкой, но не перпендикулярной его оси

.

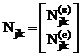Если равномерно распределённая нагрузка перпендикулярна оси стержня, то продольную силу на таком грузовом участке берут в одном, произвольно взятом, сечении. При отсутствии нагрузки поперечную и продольную силы также фиксируют в одном сечении грузового участка.

В соотношении (16.22) L_F – матрица внутренних усилий в основной системе метода сил от заданной нагрузки.

L_F = [L_F1 L_F2 … L_Fj … L_Fp], .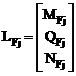

Число строк в блоках M_Fj, Q_Fj, N_Fj матрицы L_F также зависит от вида нагрузки, количества грузовых участков заданной системы и совпадает с числом строк блоков M_j, Q_j, N_j матрицы L. Количество столбцов матрицы L_F равно числу комбинаций силовых воздействий р.

В матричных соотношениях (16.21) и (16.22) В – матрица внутренней упругой податливости сооружения.

.

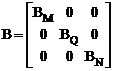В_М – матрица упругой податливости, учитывающая изгибные деформации элементов сооружения. Для грузового участка с постоянной изгибной жёсткостью поперечного сечения (EJ_k = const) при наличии на нём равномерно распределённой нагрузки

,

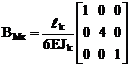при отсутствии нагрузки –

.

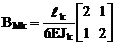B_Q – матрица упругой податливости, учитывающая деформации сдвига элементов системы. На k-ом участке с равномерно распределённой нагрузкой в случае GA_k = const

,

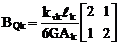без такой нагрузки –

.

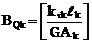B_N – матрица упругой податливости, учитывающая деформации растяжения-сжатия сооружения. Если равномерно распределённая нагрузка не перпендикулярна оси k-го грузового участка, то

,

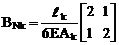если же такого рода нагрузка действует перпендикулярно оси грузового участка или вообще отсутствует на нём, то

.

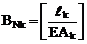Из системы канонических уравнений (16.20) получим матрицу неизвестных метода сил:

X = –d^-1 D_F. (16.23)

d^-1 – матрица, обратная по отношению к матрице внешней податливости d. Из линейной алгебры известно, что

d × d^-1 = Е,

где Е – единичная матрица.

Подставляя соотношение (16.21) и (16.22) в матричное выражение (16.23), получим:

X = –(L^T B L)^-1 (L^T B L_F). (16.24)

Вычислив матрицу усилий в лишних связях сооружения Х и используя матрицы L и L_F, элементы которых есть внутренние усилия (изгибающие моменты, поперечные и продольные) от X₁ = 1, X₂ = 1, …, X_j = 1, …, X_n = 1 и заданной нагрузки, в соответствии с принципом независимости действия сил, получим:

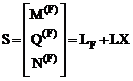. (16.25)

S – матрица внутренних усилий (изгибающих моментов M^(F), поперечных Q^(F) и продольных N^(F) сил в заданном сооружении от силового воздействия. Число строк этой матрицы совпадает с числом строк матрицы L и L_F, а число столбцов – с числом столбцов матрицы L_F, т.е. с количеством комбинаций внешних воздействий.

С учётом выражения (16.24) матричное соотношение (16.25) в окончательной форме запишется:

S = L_F – L(L^TBL)^-1(L^TBL_F). (16.26)

Для кинематической проверки расчёта заданного статически неопределимого сооружения на силовое воздействие производится сопряжение окончательных эпюр внутренних усилий, описываемых элементами матрицы S, с эпюрами внутренних усилий в единичных состояниях основной системы метода сил, описываемых элементами матрицы L. Если расчёт произведён правильно, то результат сопряжения вышеупомянутых эпюр в матричной форме даст нулевую матрицу, т.е.

L^T B S = 0. (16.27)

В расчётах плоских статически неопределимых рамных и балочных систем в соотношениях (16.26) и (16.27) матрицы L, L_F будут содержать блоки, учитывающие только изгибающие моменты, а матрица В – только элементы, соответствующие изгибным деформациям сооружения. С учётом данного обстоятельства, когда L = M, L_F = M_F, B = B_M, S = M^(F), имеем

M^(F) = M_F – M(M^T B_M M)^-1(M^T B_M M_F), (16.28)

M^T B_M M^(F) = 0. (16.29

Пример расчёта статически неопределимой рамы методом сил в матричной форме

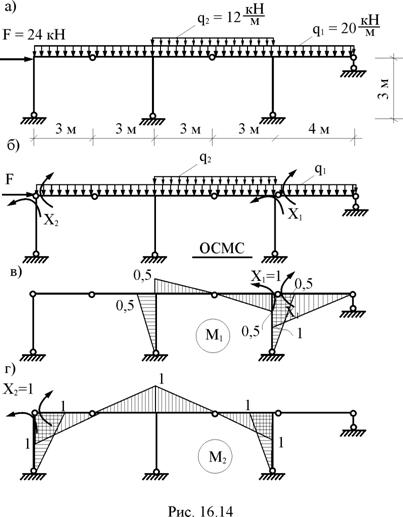
В раме, показанной на рис. 16.14,а, построить эпюры внутренних усилий отдельно от постоянной равномерно распределённой нагрузки q₁ = 20 кН/м, первой временной равномерно распределённой нагрузки q₂ = 12 кН/м, второй временной нагрузки – сосредоточенной силы F = 24 кН, а также вычислить расчётные изгибающие моменты в её характерных сечениях. Соотношение между изгибными жесткостями поперечных сечений ригеля и стоек задано: EJ_p : EJ_c = 2 : 0,5.

Порядок расчёта рамы на заданные воздействия в матричной форме определяется соотношением (16.28):

M^(F) = M_F – M(M^T B_M M)^-1(M^T B_M M_F).

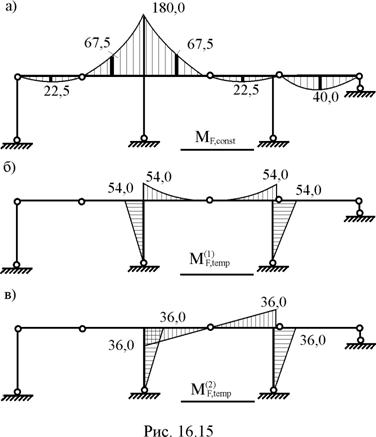
1. Подготовительный этап расчёта: определение степени статической неопределимости рамы (n_st = 3 × 3 – 7 = 2), выбор основной системы метода сил (рис. 16.14,б), построение эпюр изгибающих моментов в основной системе от Х₁ = 1, Х₂ = 1 (рис. 16.14,в,г), постоянной нагрузки (рис. 16.15,а), первой временной (рис. 16.15,б) и второй временной нагрузки (рис. 16.15,в).

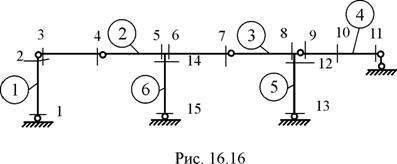
2. Нумерация грузовых участков и сечений, необходимых для формирования матриц изгибающих моментов M и M_F (рис. 16.16).

3. Формирование матриц изгибающих моментов M и M_F от Х₁ = 1, Х₂ = 1 и заданных нагрузок (постоянной и временных) в основной системе метода сил в соответствии с принятой нумерацией грузовых участков и сечений. Правило знаков для элементов этих матриц было сформулировано ранее (см. пример 13.4.1 тринадцатой лекции).

4. Формирование матрицы внутренней упругой податливости рамы, учитывающей изгибные деформации её грузовых участков. Примем EJ_p = 2EJ, EJ_с = 0,5EJ (EJ – произвольное число).

,

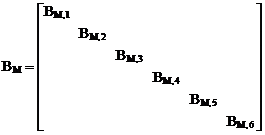где ;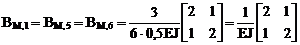

; .

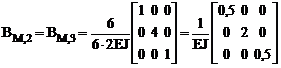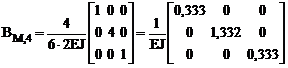5. Вычисление элементов матрицы внешней податливости принятой для расчёта основной системы метода сил, или матрицы коэффициентов при неизвестных d системы канонических уравнений.

d = М^T B_М М = .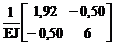

6. Вычисление элементов матрицы грузовых коэффициентов, или матрицы свободных членов D_F системы канонических уравнений

D_F = М^T B_М М_F = .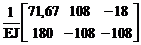

7. Обращение матрицы внешней податливости d.

d × d^-1 = Е, .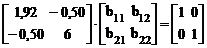

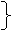1,92b₁₁ – 0,5b₂₁ = 1,

-0,5b₁₂ + 6b₂₁ = 0.

Отсюда b₁₁ = 0,533, b₂₁ = 0,044.

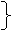1,92b₁₂ – 0,5b₂₂ = 0,

-0,5b₁₂ + 6b₂₂ = 1.

Отсюда b₁₂ = 0,044, b₂₂ = 0,170.

d^-1 = (М^T B_М М)^-1 = .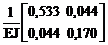

8. Вычисление элементов матрицы неизвестных метода сил Х.

X = –d^-1 D_F = –(М^T B_М М)^-1(М^T B_М М_F) =

= =

= .

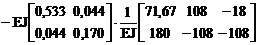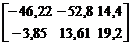9. Вычисление элементов матрицы изгибающих моментов M^(F) в заданной раме от постоянной и временной нагрузок.

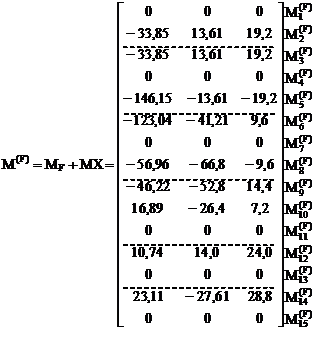
10. Кинематическая проверка правильности вычисления элементов матрицы M^(F), являющихся ординатами эпюр изгибающих моментов в заданной раме от постоянной, первой и второй временных нагрузок в сечениях, показанных на рис. 16.16.

.

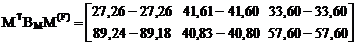Относительные погрешности вычислений при сопряжении окончательных эпюр изгибающих моментов, описываемых элементами матрицы M^(F), с соответствующими эпюрами от Х₁ = 1 и Х₂ = 1 в основной системе метода сил, описываемых элементами матрицы М, не превышают 0,07 %.

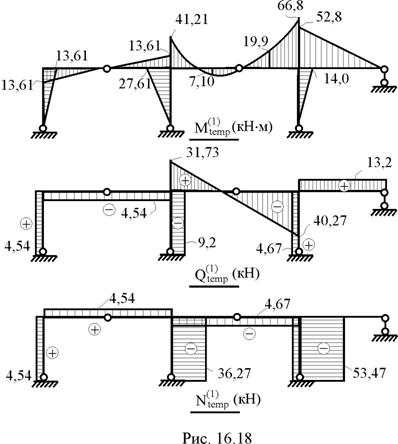
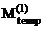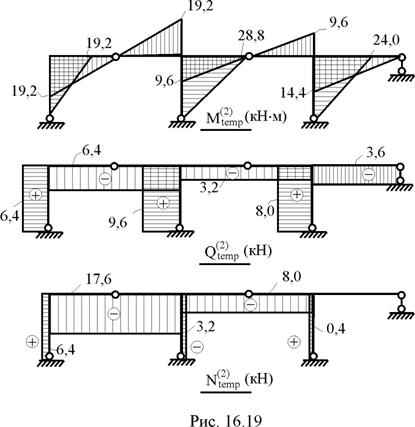
11. Построение эпюр изгибающих моментов в заданной раме M_const от постоянной нагрузки q₁ = 20 кН/м – по элементам первого столбца матрицы M^(F) (рис. 16.17); от первой временной нагрузки q₂ = 12 кН/м – по элементам второго столбца матрицы M^(F) (рис. 16.18); 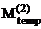от второй временной нагрузки F = 24 кН – по элементам третьего столбца матрицы M^(F) (рис. 16.19).

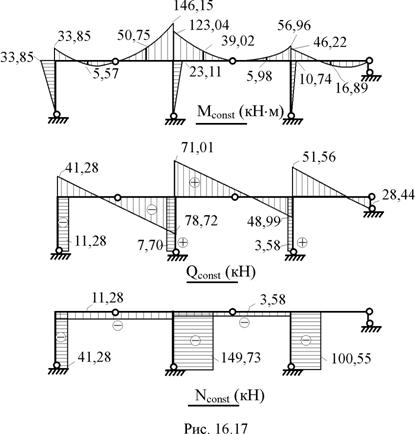
12. Построение эпюр поперечных (Q_const, 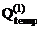, 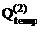) и продольных сил (N_const, 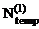, 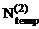) от каждого из вышеупомянутых воздействий (рис. 16.17, 16.18, 16.19).

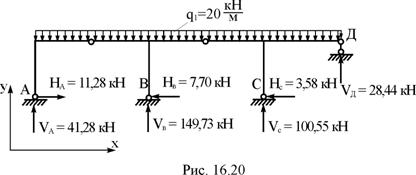
13. Статическая проверка условий равновесия рамы в целом. Здесь эту проверку проведём только в случае действия постоянной нагрузки (рис. 16.20).

åF_x = 0, 11,28 – 7,70 – 3,58 = 0, 0 º 0;

åF_y = 0, 41,28 + 149,73 + 100,55 + 28,44 – 20×16 = 0, 0 º 0;

åmom(F)_B = 0, 41,28×6 – 100,55×6 – 28,44×10 – 20×6×3 +

+ 20×10×5 = 1247,68 – 1247,70 = –0,02.

Относительная погрешность вычислений при проверке последнего условия равновесия составляет

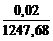× 100 % = 0,0016 %.

14. Вычисление расчётных изгибающих моментов в характерных сечениях рамы (табл. 2).

Таблица 2

№ сечений	Изгибающие моменты, кН×м	Расчётные изгибающие моменты, кН×м
Mconst		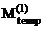	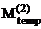max	min
	-33,85	13,61	19,2	-1,04	-33,85
	-146,15	-13,61	-19,2	-146,15	-178,96
	-123,04	-41,21	9,6	-113,44	-164,25
	-56,96	-66,8	-9,6	-56,96	-133,36
	-46,22	-52,8	14,4	-31,82	-99,02
	16,89	-26,4	7,2	24,09	-9,51
	10,74	14,0	24,0	48,74	10,74
	23,11	-27,61	28,8	51,91	-4,50
	-33,85	13,61	19,2	-1,04	-33,85

Вопросы для самопроверки

1. Что называется основной системой метода сил?

2. Какие приёмы используются для удаления лишних связей из заданного статически неопределимого сооружения?

3. В каком случае основная система метода сил для заданного статически неопределимого сооружения будет статически определимой?

4. Сформулируйте требования, предъявляемые к основной системе метода сил. Выполнение какого требования является абсолютно обязательным при выборе основной системы?

5. Для заданного преподавателем статически неопределимого сооружения, испытывающего силовое воздействие, запишите в общем виде систему канонических уравнений метода сил, используя статически определимую основную систему. Поясните физический смысл i-го уравнения этой системы.

6. Какой смысл имеют неизвестные метода сил X₁, X₂, …, X_j, …, X_n?

7. Поясните физический смысл входящих в систему канонических уравнений произведений чисел d_iiX_i и d_ijX_j?

8. Какой физический смысл имеют коэффициенты при неизвестных d_ii и d_ij, а также грузовые коэффициенты D_iF системы канонических уравнений метода сил? Как определяются эти коэффициенты для плоских стержневых систем в общем случае? Какие упрощения при вычислении коэффициентов d_ii, d_ij и D_iF имеют место в плоских рамных и балочных системах?

9. Как проверить правильность вычисления коэффициентов при неизвестных и свободных членов системы канонических уравнений метода сил?

10. Каким образом при силовом воздействии вычисляются внутренние усилия в заданном статически неопределимом сооружении, если известны усилия в лишних связях этого сооружения X₁, X₂, …, X_j, …, X_n: для плоских стержневых систем в общем случае? для плоских рамных и балочных систем?

11. Как производится проверка правильности эпюр внутренних усилий при силовом воздействии, полученных: для произвольной плоской статически неопределимой стержневой системы? для плоской рамной или балочной системы?

12. Запишите в общем виде систему канонических уравнений метода сил в матричной форме, а также матричные соотношения для вычисления элементов: матрицы внешней податливости сооружения d, матрицы грузовых коэффициентов системы канонических уравнений D_F, матрицы неизвестных метода сил Х, матрицы внутренних усилий в заданном статически неопределимом сооружении S.

13. Какой смысл имеют элементы матриц L, L_F, B, S? Какие блоки (подматрицы) включают в себя матрицы L, L_F, B, S?

14. Определите число строк и столбцов в матрицах L, L_F, B для конкретной плоской стержневой системы с заданным силовым воздействием.

15. Каким образом проверяется правильность вычисления элементов матрицы внутренних усилий в заданном статически неопределимом сооружении при силовом воздействии?

16.10. Рекомендуемая литература

1. Леонтьев Н.Н. Основы строительной механики стержневых систем: Учеб. для вузов / Н.Н. Леонтьев, Д.Н. Соболев, А.А. Амосов. – М.: Изд-во ассоциации строительных вузов, 1996. – 541 с.

Гл. 6. Метод сил. § 6.1. Основная идея метода сил. § 6.2. Лишние неизвестные. Выбор основной системы метода сил. § 6.3. Канонические уравнения метода сил и их свойства. § 6.4. Вычисление коэффициентов и свободных членов канонических уравнений и их проверка. § 6.5. Построение окончательных эпюр внутренних усилий. Статическая и кинематическая проверки. – С. 124–134. § 6.7. Пример расчета статически неопределимой рамы методом сил. – С. 136–140. § 6.10. Матричная форма метода сил. – С. 149–151.

2. Дарков А.В. Строительная механика: Учеб. для вузов / А.В. Дар­ков, Н.Н. Шапошников. – М.: Высш. школа, 1986. – 607 с.

Гл. 6. Расчёт статически неопределимых систем методом сил. § 6.2. Канонические уравнения метода сил. § 6.3. Расчёт статически неопределимых систем на действие заданной нагрузки. – С. 199–213. § 6.7. Построение эпюр поперечных и продольных сил. Проверка эпюр. – С. 222–228. § 6.14. Проверка коэффициентов и свободных членов системы канонических уравнений. § 6.15. Примеры расчёта рам. – С. 247–260.

3. Смирнов А.Ф. Строительная механика. Стержневые системы: Учеб. для вузов / А.Ф. Смирнов, А.В. Александров, Б.Я. Лаще­ни­ков, Н.Н. Шапошников. – М.: Стройиздат, 1981. – 512 с.

Гл. XI. Метод сил. § 59. Канонические уравнения и их особенности. § 60. Общий алгоритм расчёта. – С. 316–332. § 64. Расчёт статически неопределимых систем в матричной форме. – С. 368–381.

4. Клейн Г.К. Руководство к практическим занятиям по курсу строительной механики. Статика стержневых систем: Учеб. пособие / Г.К. Клейн, Н.Н. Леонтьев. – М.: Высш. школа, 1980. – 384 с.

Гл. IX. Расчёт рам методом сил. § IX.1. Порядок расчёта рам. – С. 137–145. § IX.7. Расчёт рам в матричной форме. – С. 169–181.

5. Анохин Н.Н. Строительная механика в примерах и задачах. Ч. 2. Статически неопределимые системы: Учеб. пособие / Н.Н. Анохин. – М.: Изд-во ассоциации строительных вузов, 2000. – 464 с.

Гл. 5. Расчёт сооружений методом сил. § 5.1. Основная идея метода сил. Выбор рациональной основной системы. Примеры 5.1–5.5. – С. 8–15. § 5.2. Силовое воздействие. Примеры 5.12–5.13. – С. 23–35.

6. Проценко В.М. Расчёт статически неопределимых рам: Методические указания / В.М. Проценко, В.Г. Себешев. – Новосибирск: НГАС, 1993. – 56 с.

Задача № 1. Расчёт плоской статически неопределимой рамы методом сил. – С. 1–28.