Критерий наибольших нормальных напряжений

По этой теории причиной разрушения материала считается наибольшее (из трех главных) нормальное напряжение при этом действие двух других напряжений не учитывается.

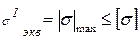. (3.12)

Данная теория прочности в настоящее время практически не используется, так как она подтверждается экспериментально лишь для некоторых очень хрупких материалов (камень, кирпич, керамика и т.д.)

Критерий наибольших линейных деформаций

По второй теории прочности, в качестве критерия прочности принимают наибольшую по абсолютной величине линейную деформацию .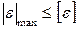

Выражая деформации через обобщенный закон Гука получим:

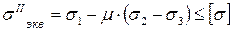. (3.13)

Данная теория редко применяется в инженерной практике, так как находит экспериментальное подтверждение лишь для некоторых хрупких материалов (легированный чугун, высокопрочная сталь).

Критерий наибольших касательных напряжений

В качестве критерия прочности принята величина наибольшего касательного напряжения .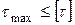

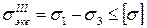. (3.14)

Третья теория прочности хорошо подтверждается опытами для материалов, одинаково работающих на растяжение и сжатие. Недостаток ее заключается в том, что она не учитывает среднего по величине главного напряжения 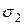, которое как показывают эксперименты, также оказывает, хотя и незначительное, влияние на прочность материалов.

Критерий удельной потенциальной энергии формоизменения

В качестве критерия прочности в этом случае принимают количество удельной потенциальной энергии формоизменения, накопленной деформированным элементом.

Выразив удельную потенциальную энергию формоизменения через главные напряжения при объемном напряженном состоянии получим:

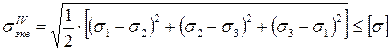. (3.15)

Опыты хорошо подтверждают четвертую теорию для пластичных материалов, одинаково работающих на растяжение и сжатие. При этом четвертая теория более точно, чем третья, описывает появление в материале малых пластических деформаций.

Теория Мора

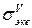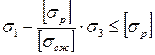= (3.16)

где 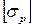- допускаемое напряжение на растяжение; 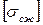- на сжатие.

Теория прочности Мора позволяет установить сопротивление разрушению материалов, обладающих разными сопротивлениями растяжению и сжатию (хрупкие материалы). Опыты показывают, что достаточно точные результаты гипотеза Мора дает для напряженных состояний смешанного типа, то есть для тех случаев, когда главные нормальные напряжения имеют разные знаки.

Таким образом, для практических расчетов следует рекомендовать третью и четвертую теории прочности для материалов одинаково работающих на растяжение и сжатие, и теорию Мора – для материалов, различно сопротивляющихся растяжению и сжатию, то есть для хрупких материалов.

Сдвиг