Тема 2.6. Понятие о касательных напряжениях при изгибе. Линейные и угловые перемещения при изгибе, их определение

Иметь представление о касательных напряжениях при изги­бе, об упругой линии балки, о деформациях при изгибе и методах определения линейных и угловых перемещений.

Знать один из методов определения линейных и угловых пере­мещений.

Поперечный изгиб. Внутренние силовые факторы.Напряжения.

Рассмотрим изгиб балки, защемленной справа и нагруженной сосредоточенной силой F (рис. 33.1).

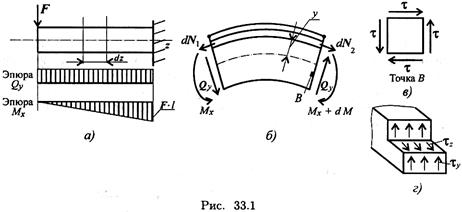
В поперечном сечении возникает изгибающий момент, меняю­щийся по длине балки, и постоянная поперечная сила Q.

Рассмотрим участок балки длиной dz (рис. 33.15).

Изгибающий момент, как известно, является равнодействующим элементарных моментов, возникающих в результате действия про­дольных сил упругости. Связь между нормальными напряжениями в точках поперечного сечения и изгибающим моментом уже рассмат­ривалась:

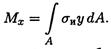
Поперечная сила представляет собой равнодействующую ка­сательных сил упругости, возникающих в поперечных сечениях (рис. 33.1 в), и связана с касательными напряжениями зависимостью

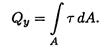
В силу парности касательных напряжений в продольных сече­ниях балок, параллельных нейтральному слою, возникают такие же по величине касательные напряжения (рис. 33.1 г).

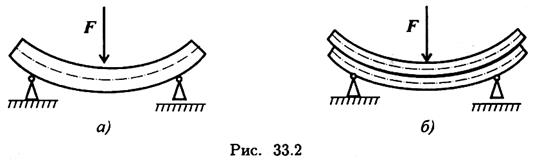
Появление касательных напряжений в продольных слоях балок подтверждается следующим опытом. Рассмотрим поперечный изгиб двух балок, одна — цельная, другая — составленная из нескольких положенных друг на друга слоев (рис. 33.2). Цельная балка изогнет­ся (рис. 33.2а), брусья второй балки сдвинутся (рис. 33.2б). Каждый из брусьев деформируется независимо. В цельной балке сдвигу слоев препятствуют возникающие касательные напряжения.

На поверхности касательные напряжения равны нулю.

Формула для расчета касательных напряжений для балки квад­ратного сечения была получена в 1855 году русским инженером Д. И. Журавским,

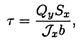
где Q_y — поперечная сила в сечении; S_x — статический момент отсе­ченной части относительно оси х, S_x = А_отсу_с, А_0ТС – площадь попе­речного сечения отсеченной части (рис. 33.3); J_x — момент инерции сечения; b — ширина балки.

Наибольшее значение каса­тельного напряжения достигается на нейтральной оси:

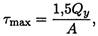
А — площадь сечения.

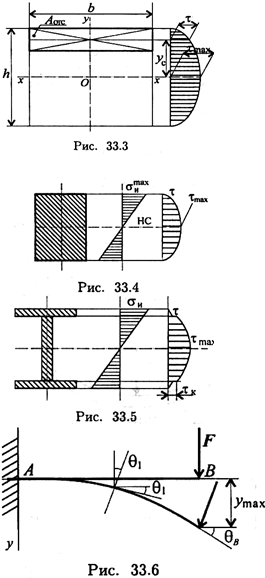Максимальное напряжение при поперечном изгибе в полтора раза больше среднего значения

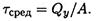
Обнаруживается, что макси­мальные нормальные напряжения в сечении не совпадают с максимальны­ми касательными (рис. 33.4).

Для длинных балок расчет про­водят только по нормальным напряжениям, т. к. касательные здесь незначительны. Для коротких балок, нагруженных значительными попереч­ными силами вблизи опор, проводят расчет по касательным напряжениям. Однако для тонкостенных профилей (двутавр, швеллер) необходимо проверять прочность балки в точках, где полка сочленяется со стен­кой. Здесь и нормальные, и касательные напряжения значительны (рис. 33.5).

Понятия о линейных и угловых перемещениях при изгибе

Под действием поперечных нагрузок продольная ось искривля­ется (рис. 33.6). Если материал подчиняется закону Гука, после сня­тия нагрузок брус выпрямляется, поэтому изогнутую ось бруса назы­вают упругой линией. По форме упругой линии балки можно судить о перемещениях при изгибе.

При прямом поперечном изгибе бруса его ось, искривляясь, оста­ется в силовой плоскости. В результате деформации бруса каждое из его поперечных сечений получает вертикальное и горизонтальное перемещение, а само сечение поворачивается на некоторый угол Θ.

Деформации должны иметь упругий характер, они достаточно малы. В этом случае горизонталь­ные перемещения сечений ничтожно малы и не учитываются. Рассмат­ривают вертикальные перемещения центра тяжести сечения, называе­мые прогибами (у). Максимальные прогибы обозначают f = у_таx. Для обеспечения нормальной работы устанавливаемого на балках оборудования проводят расчет на жесткость.

Условие жесткости выражается неравенством

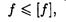
где f — максимальный расчетный прогиб балки; [f] — допускаемый прогиб. Иногда проверяется угол поворота сечения Θ < [Θ]. Допускаемый прогиб невелик: от 1/200 до 1/1000 пролета балки; допускаемый угол поворота 1*10^-3 рад.

Существует несколько методов определения перемещений сече­ний при изгибе. Один из них основан на дифференцировании урав­нения упругой линии, более рациональный способ — использование интегралов Мора. Метод Мора — универсальный способ определения линейных и угловых перемещений в любых системах.

Для облегчения расчетов на жесткость можно использовать формулы прогибов и углов поворота сечений балок для простейших случаев нагружений. Наиболее распространенные случаи нагружения и расчетные формулы приведены в таблице.

При решении используем принцип независимости действия сил. Заданный случай нагружения делится на составляющие, для кото­рых прогибы рассчитываются по известным табличным формулам, результаты расчетов суммируются.

Ограничение угла поворота вводится для обеспечения нормаль­ной работы подшипников скольжения и роликовых подшипников.

В этом случае проверяется дополнительное условие жесткости:

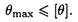
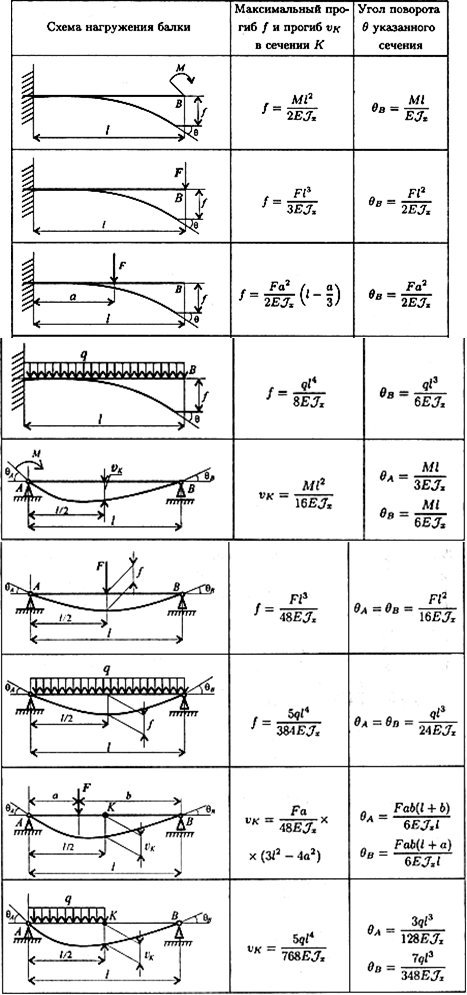Таблица 33.1.Формулы для определения прогибов и углов поворота сечений балок

Примеры решения задач

Пример 1. Проверить жесткость двутавровой балки (рис. 33.7). Принять

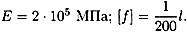
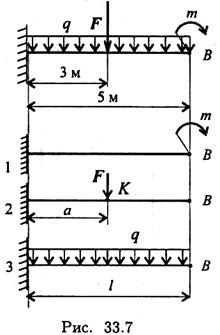Сечение балки — двутавр № 45.

Решение

Используем принцип независимости действия сил. По приведен­ным в таблице формулам рассчитываем прогиб балки в точке от каждого вида нагружения отдельно (рис. 33.7 (1, 2, 3)).

Поскольку все действующие нагрузки прогибают балку вниз, результаты дей­ствия нагрузок можно сложить. Получен­ный суммарный прогиб сравним с допус­каемым прогибом.

Допускаемый прогиб

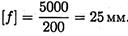
Суммарный прогиб

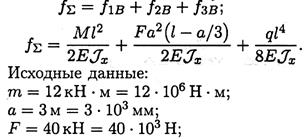
q = 4кН/ м = 4Н/мм; l = 5м = 5-10³мм.

Для двутавра № 45 ГОСТ 8239-89

J_x = 27696 см⁴ = 27,7 • 10⁷мм⁴.

Тогда

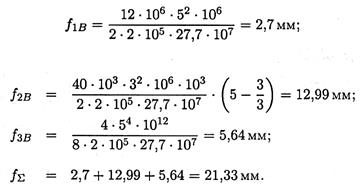
21,33 < 25 — условие жесткости выполняется.

Максимальный прогиб не превышает допускаемого значения.

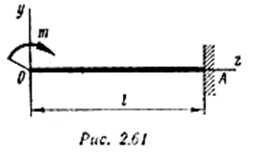
Пример 2. Определить угол поворота и прогиб свободного конца консольной балки, изображенной на рис. 2.61.

Решение

Поместим начало координат на левом конце балки и составим обобщенные уравнения упругой линии и углов поворота:

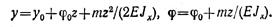
Определяем начальные параметры у₀ и ф₀ исходя из условий опорных закреплений:

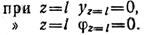
Из второго условия находим φ₀:

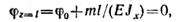откуда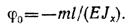

Знак минус перед значением угла поворота показы­вает, что поворот начального сечения происходит по ча­совой стрелке. Из второго условия находим у₀:

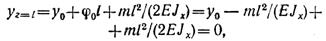
Откуда

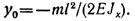
Знак минус перед значением прогиба показывает, что он направлен вниз, противоположно положительному на­правлению оси у.

Пример 3. Определить прогиб посередине пролета балки, нагруженной равномерно распределенной нагруз­кой (см. рис. 2.51, а).

Решение

Поместим начало координат на левой опоре балки и составим обобщенные уравнения упругой линии и углов поворота:

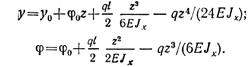
Определяем начальные параметры y₀ и φ₀ исходя из условия опорных закреплений:

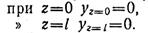
Из первого условия находим у₀ = 0.

Из второго условия определяем φ₀:

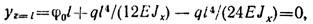
Откуда

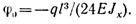
Подставляя у₀ и φ₀ в уравнение прогибов, получаем

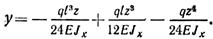
В середине пролета при z = 0,5l прогиб принимает максимальное значение

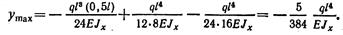
Знак минус перед значением прогиба показывает, что он направлен вниз, т. е, в сторону, противоположную по­ложительному направлению оси у.

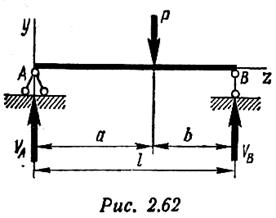
Пример 4. Для балки, изображенной на рис. 2.62, опре­делить прогиб под точкой при­ложения силы и углы поворота на опорах А и В.

Решение

Поместим начало координат на опоре A. Раз­обьем балку на два участка и составим обобщенные уравне­ния упругой линии и углов по­ворота для каждого из них, предварительно определив опорные реакции:

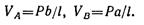
для первого участка

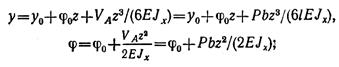
для второго участка

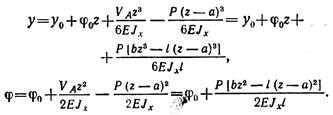
Определяем начальные параметры исходя из условий опорных закреплений:

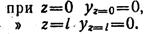
Из первого уравнения находим у₀:

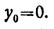
Из уравнения прогибов для второго участка находим угол поворота φ₀ сечения на левой опоре:

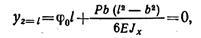
Откуда

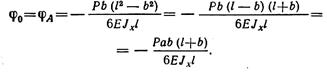
Подставив значение φ₀ в уравнение прогибов первого участка, получим

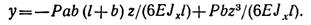
При z = a найдем прогиб сечения под точкой прило­жения силы Р:

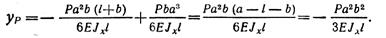
Используя уравнение углов поворота для второго участка

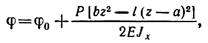
найдем при z = l угол поворота сечения на правой опоре В:

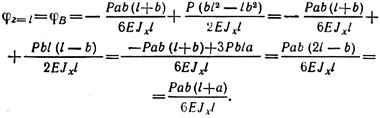
Угол поворота φ_В положителен, следовательно, он в отличие от угла поворота φ_А направлен против часовой стрелки.

При приложении силы Р посередине пролета балки, т. е. при а = b = l/2, углы поворота опорных сечений и про­гиб под точкой приложения силы примут значения:

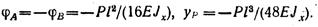
Пример 5. Определить максимальный прогиб двухопорной балки, нагруженной равномерно распределенной по всему пролету нагрузкой интенсивностью q и сосредоточенной силой Р посередине пролета.

Решение

Наибольший прогиб при симметричном нагружёный балки возникает посередине пролета, под точ­кой приложения силы Р. Этот прогиб может быть найден на основе принципа независимости действия сил как сумма прогибов от распределенной нагрузки интенсивностью q и сосредоточенной силы Р:

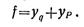
Составляющие части полного прогиба были вычислены в предыдущих примерах. Подставляя их значения, полу­чаем

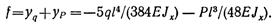
Оба составляющих прогиба направлены вниз и входят поэтому со знаком минус.