Глава 6. перемещения при изгибе

6.1. Метод Мора для определения перемещений

Если материальная точка находится в равновесии под действием некоторой системы сил (рис. 6.1), то сумма работ этих сил на любом возможном перемещении равна нулю.

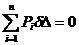. (6.1)

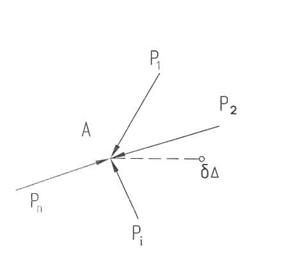
Рис. 6.1

Любое упругое тело можно рассматривать как систему материальных точек, находящихся в равновесии под действием внешних и внутренних сил упругости. Следовательно, работа всех внешних и внутренних сил упругости на любом возможном перемещении для упругого тела равна нулю.

Пусть под воздействием внешних сил 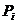в балке возникли действительные перемещения 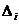, и под действием внешних и внутренних сил упругости оно находится в равновесии (рис. 6.2,а). Назовем его действительным состоянием (I состояние). Представим себе II состояние (фиктивное), в котором все силы есть вариации сил действительного состояния, тогда и перемещения в нем будут вариациями перемещений первого состояния (рис. 6.2,б). Составим работу сил первого состояния на перемещениях второго.

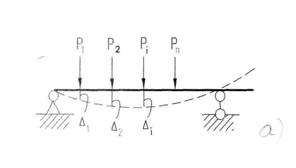
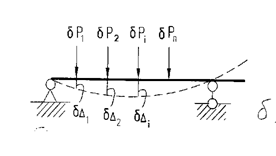
Рис. 6.2

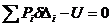, (6.2)

где 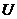— работа внутренних сил. Тогда можно записать

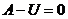. (6.3)

Возьмем теперь два состояния упругой системы (рис. 6.3).

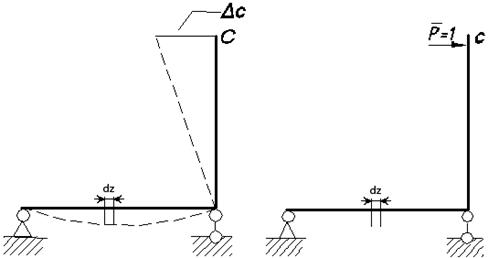
Рис. 6.3

Рассматривая перемещения точек состояния I (рис. 6.3,а) как возможные, составим на основании принципа Лагранжа работу II — состояния (рис. 6.3,б) на перемещениях I.

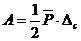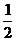, ( — связана со статическим приложением силы)

или 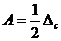. (6.4)

Вычислим работу внутренних силовых факторов второго состояния на перемещениях первого. Для этого из I и II состояний вырежем участок бруса длиной 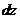(рис. 6.3).

Элементарная работа внутренних сил II состояния на перемещениях I, равна:

.

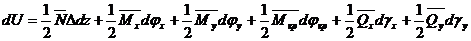Деформации малого элемента 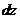определяются по известным формулам.

При растяжении: .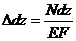

При изгибе, кручении: , , .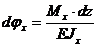

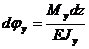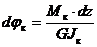При сдвиге: .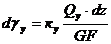

Абсолютный сдвиг: ; ; ; .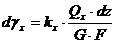

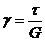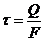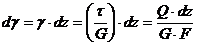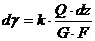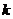Т.к. касательные силы распределены по сечениям неравномерно то , где — поправочный коэффициент, учитывающий неравномерное распределение касательных напряжений (рис. 6.4).

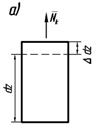
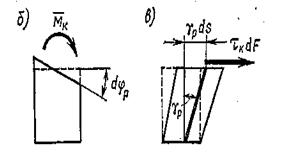
Рис. 6.4

Подставляя перемещения в выражения для 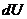, получим:

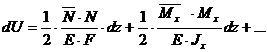
Для всей системы

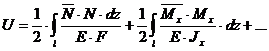
Подставляя в уравнение Лагранжа (6.3), получим

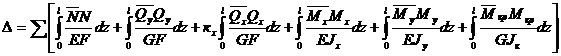(6.5)

В правой части этого выражения стоят интегралы Мора.

Если определяются перемещения в пространственных системах, то первыми тремя интегралами пренебрегают.

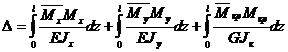(6.6)

Если определять перемещения в плоских балках, рамах, то

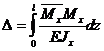(6.7)

Если определять перемещения в фермах, то

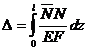(6.8)

Способ Верещагина

Основным недостатком при определении перемещений с помощью интегралов Мора является необходимость составлять аналитические выражения подынтегральных функций и дальнейшего их интегрирования. Это особенно неудобно при большом количестве участков, т.к. приводит к громоздким вычислениям.

Если брус состоит из прямых участков с постоянной, в пределах каждого участка жесткостью, то операцию вычисления интегралов Мора можно упростить. Это упрощение основано на том, что эпюры от единичных силовых факторов на прямолинейных участках бруса всегда будут линейными.

Пусть на участке длиной 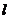нужно взять интеграл от произведения двух функций

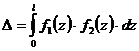(6.9)

при условии, что по крайне мере одна из функций — линейная. Пусть 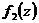— линейная, тогда 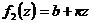(рис.6.5).

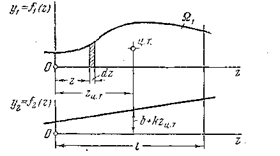
Рис. 6.5

Тогда выражение (6.9) примет вид 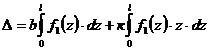. Первый из интегралов представляет собой площадь ограниченную кривой 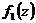, т.е. площадь криволинейной эпюры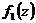

.

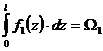Второй интеграл представляет собой статический момент этой площади 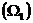относительно 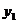, т.е.

,

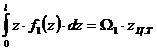где 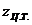— координата центра тяжести первой эпюры.

В результате получим

.

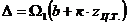Но .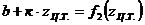

Следовательно 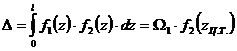. (6.10)

Таким образом, по способу Верещагина операция интегралов заменяется перемножением площади первой эпюры на ординату второй (линейной) эпюры взятую под центром тяжести первой. Если обе функции линейные, то операция перемножения обладает свойством коммутативности.

На первый взгляд способ Верещагина не дает существенных упрощений, т.к. его применение требует построения эпюр внутренних усилий от заданной и единичных сил и перемножения их. Однако почти все встречающиеся на практике эпюры внутренних усилий могут быть, как правило, разбиты на три простейшие фигуры: прямоугольник, треугольник и параболу (рис. 6.6).

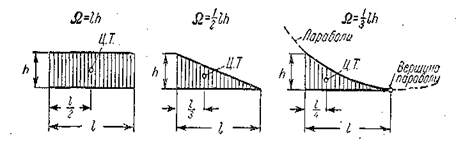
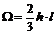
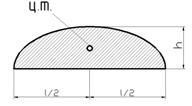
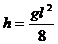
Рис. 6.6