Тема 4. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ
И ЕГО ПРИМЕНЕНИЕ К ИССЛЕДОВАНИЮ ФУНКЦИИ
Изучение этой темы следует начать с разбора решений задач, приводящих к понятию производной. Это позволит осмыслить и понять определение производной, условия ее существования, ее геометрический и механический смыслы. Особое внимание необходимо обратить на теоремы и правила, позволяющие упростить вычисление производных. Успешное применение производной при решении задач зависит от усвоения понятий возрастания и убывания функций, наибольших и наименьших значений функции, экстремумов функции, выпуклости и вогнутости кривой.
Вопросы программы для изучения и самопроверки
1. Производная функции, ее геометрический смысл.
2. Правила дифференцирования функций.
3. Производная сложной, неявно заданной и обратной функций.
4. Дифференцирование функций, заданных параметрически.
5. Дифференциал функции.
6. Производные и дифференциалы высших порядков.
7. Теоремы Ролля, Лагранжа, Коши. Правило Лопиталя.
8. Условия возрастания и убывания функций. Экстремум функции. Необходимое условие экстремума. Достаточные признаки существо- вания экстремума.
9. Наибольшее и наименьшее значения непрерывной на отрезке функции.
10. Выпуклость и вогнутость графика функции. Точки перегиба.
11. Асимптоты кривых.
Задачи 81–100.Найти производные заданных функций.
81. а) 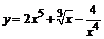 ; ; | б) 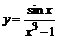 ; ; |
в) 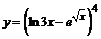 . . | |
82. а) 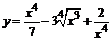 ; ; | б) 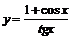 ; ; |
в) 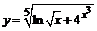 . . | |
83. а) 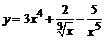 ; ; | б) 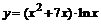 ; ; |
в) 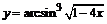 . . | |
84. а) 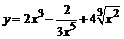 ; ; | б) 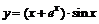 ; ; |
в) 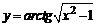 . . | |
85. а) 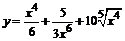 ; ; | б) 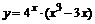 ; ; |
в) 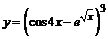 . . | |
86. а) 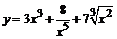 ; ; | б)  ; ; |
в) 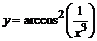 . . | |
87. а) 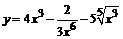 ; ; | б) 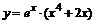 ; ; |
в) 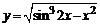 . . | |
88. а) 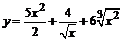 ; ; | б) 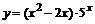 ; ; |
в) 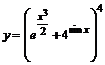 . . | |
89. а) 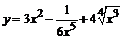 ; ; | б) 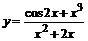 ; ; |
в) 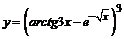 . . | |
90. а) 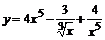 ; ; | б) 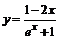 ; ; |
в) 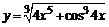 . . | |
91. а) 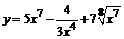 ; ; | б) 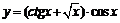 ; ; |
в) 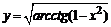 . . | |
92. а) 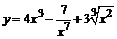 ; ; | б) 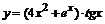 ; ; |
в) 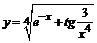 . . | |
93. а) 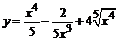 ; ; | б) 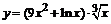 ; ; |
в) 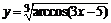 . . | |
94. а) 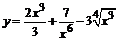 ; ; | б) 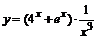 ; ; |
в) 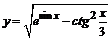 . . | |
95. а) 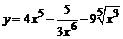 ; ; | б)  ; ; |
в) 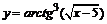 . . | |
96. а) 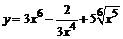 ; ; | б) 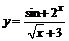 ; ; |
в) 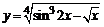 . . | |
97. а) 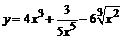 ; ; | б) 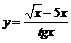 ; ; |
в) 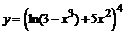 . . | |
98. а) 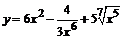 ; ; | б) 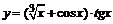 ; ; |
в) 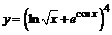 . . | |
99. а) 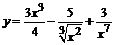 ; ; | б) 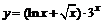 ; ; |
в) 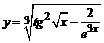 . . | |
100. а) 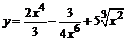 ; ; | б) 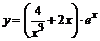 ; ; |
в) 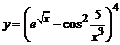 . . |
Решение типовых примеров
При решении примеров рекомендуется использовать правила дифференцирования и таблицу производных.
Таблица производных
| 1. | 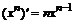 | 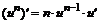 |
| 2. | 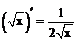 | 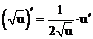 |
| 3. | 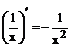 |  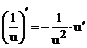 |
| 4. | 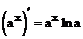 | 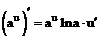 |
| 5. | 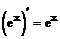 | 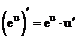 |
| 6. | 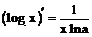 | 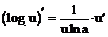 |
| 7. | 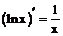 | 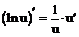 |
| 8. | 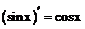 | 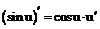 |
| 9. | 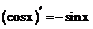 | 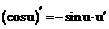 |
| 10. | 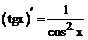 | 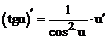 |
| 11. | 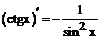 | 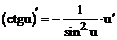 |
| 12. | 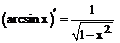 | 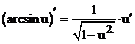 |
| 13. | 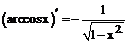 | 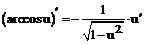 |
| 14. | 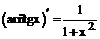 | 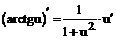 |
| 15. | 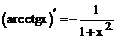 | 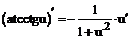 |
Правила дифференцирования
Если С – постоянная величина и функции 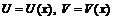 имеют производные, то:
имеют производные, то:
1. 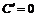 .
.
2. а) 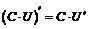 .
.
б) 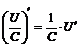 .
.
3. 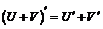 .
.
4. 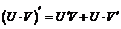 .
.
5. 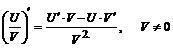
6. Производная сложной функции 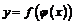 вычисляется по формуле
вычисляется по формуле 
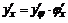 .
.
П р и м е р ы. Найти производные заданных функций:
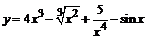 .
.
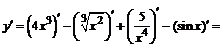
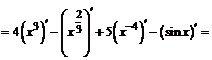
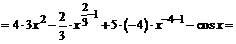
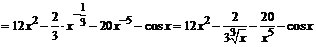 ;
;
2. 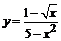 .
.
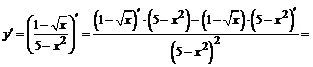
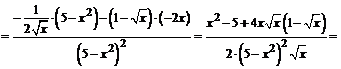
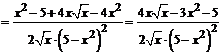 .
.
3. 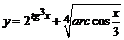 .
.
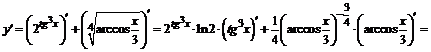
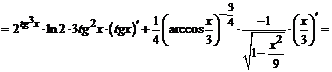
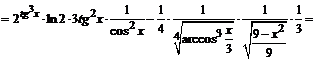
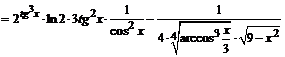 .
.
Задача 101–120.Провести полное исследование заданных функций и построить их графики.
101. 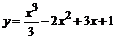 . . | 102. 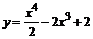 . . |
103. 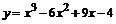 . . | 104. 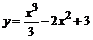 . . |
105. 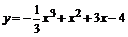 . . | 106. 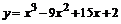 . . |
107. 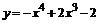 . . | 108. 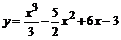 . . |
109. 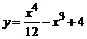 . . | 110. 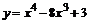 . . |
111. 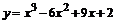 . . | 112. 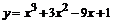 . . |
113. 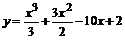 . . | 114. 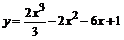 . . |
115. 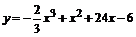 . . | 116. 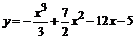 . . |
117. 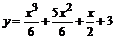 . . | 118. 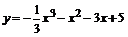 . . |
119. 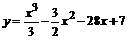 . . | 120. 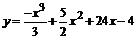 . . |
Решение типового примера
П р и м е р . Исследовать функцию 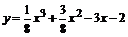 и пост -роить ее график.
и пост -роить ее график.
1. Область определения функции: 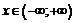 .
.
2. Так как функция является многочленом, следовательно она непрерывна.
3. Исследуем на четность и нечетность
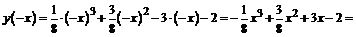
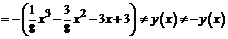 . Функция не является ни четной, ни нечетной.
. Функция не является ни четной, ни нечетной.
4. Для определения интервалов монотонности и точек экстремума находим первую производную функции
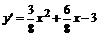 ;
; 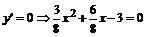 .
.
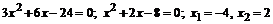 . Это критические точки. Результаты исследования знака производной и выводы сведем в таблицу:
. Это критические точки. Результаты исследования знака производной и выводы сведем в таблицу:
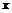 | 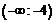 | -4 | 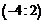 | 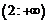 | |
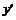 | + | – | + | ||
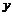 |  | mах |  | 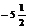 min min |  |
Представим 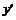 в виде произведения
в виде произведения 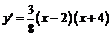 . Определим знаки
. Определим знаки 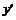 на каждом интервале:
на каждом интервале: 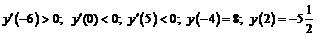 .
.
5. Для определения интервалов выпуклости и вогнутости, точек перегиба найдем вторую производную функции:
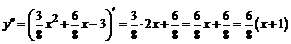 ;
;
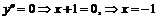 .
.
Исследуем поведение знака 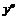 в окрестности точки
в окрестности точки 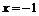 .
.
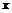 | 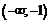 | –1 | 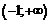 |
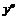 | – | + | |
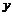 | выпукла | 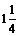 | вогнута |
Точка 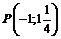 – точка перегиба.
– точка перегиба.
6. Найдем несколько дополнительных точек графика функции
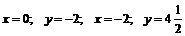 .
.
7. По результатам исследования строим график.
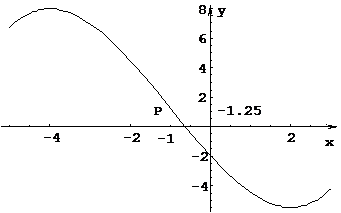
Рис. 1.
