Тема 1.1 Дифференциальное исчисление

Лекция №1.

План:

1. Производная функции, её геометрический и механический смысл. Формулы производных.

2. Изучение производных суммы, произведения, частного функций. Обоснование производных элементарных и сложных функций, обратных функций.

Определение 1: Производная есть скорость изменения функции в окрестности данной точки.

Пусть дана некоторая функция у = у(х). Ее производная определяется следующим образом:

у(х + ∆х) – у(х)

Иначе говоря, производная есть предел отношения приращения функции к бесконечно малому приращению аргумента.

Определение 2:Дифференциалом функции (аргумента) называется бесконечно малое приращение функции (аргумента).

Для той же самой функции у = у(х) дифференциалы имеют следующее обозначения: dx – дифференциал аргумента, dy – дифференциал функции.

dy

С учетом приведенных определений получаем следующую связь между производной и дифференциалами:

		(2)

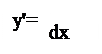- производная есть отношение дифференциала функции к дифференциалу аргумента.

Определим ГЕОМЕТРИЧЕСКИЙ СМЫСЛ производной и дифференциала. Для этого изобразим фрагмент графика некоторой довольно гладкой функции у = у(х) (рисунок 1).

dy

dx

α

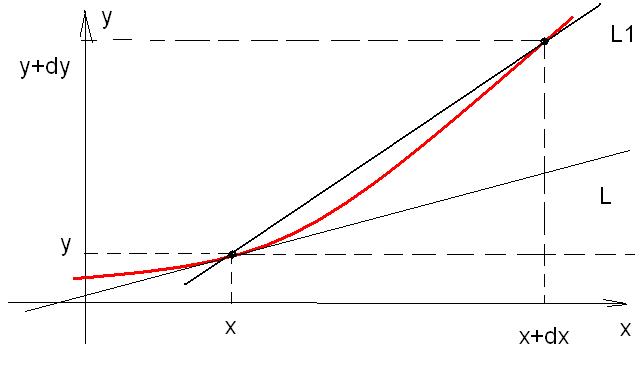
Рисунок1.

Выделим произвольную точку (х;у) на графике и построим касательную L в этой точке.

Зададимся малым приращением аргумента dx, которое, для наглядности. Изобразим покрупнее.

Определим соответствующее приращение функции ∆у и построим хорду L₁.

Видим, что при dx → 0 эта хорда, вращаясь вокруг точки (х;у), переходит в касательную L.

Таким образом, при бесконечно малом приращении dx хорда L₁ и касательная L НЕРАЗЛИЧИМЫ.

Отметим, что касательная L, совместно с координатными линиями, изображенными на рисунке, образует прямоугольный треугольник. Горизонтальный катет равен dx, вертикальный катет обозначим через dy.

dy

Видим, что при dx → 0 величина dy практически совпадает с приращением функции, ∆у → dy. То есть dy – это ДИФФЕРЕНЦИАЛ функции. Следовательно, учитывая (2) , получаем

			(3)

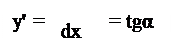- производная функции равна тангенсу угла между касательной к графику функции в данной точке и осью Ох.

На основании выше приведенных рассуждений можно дать еще одно определение дифференциала функции.

Дифференциалом функции у = у(х) называется ГЛАВНАЯ ЛИНЕЙНАЯ часть приращения функции, соответствующая бесконечно малому приращению dx ее аргумента:

∆у = dy + o(dx), (4)

где

dy = y' · dx. (5)

Пример:

Рассмотрим график некоторой произвольной функции, изображенной на рисунке 2.

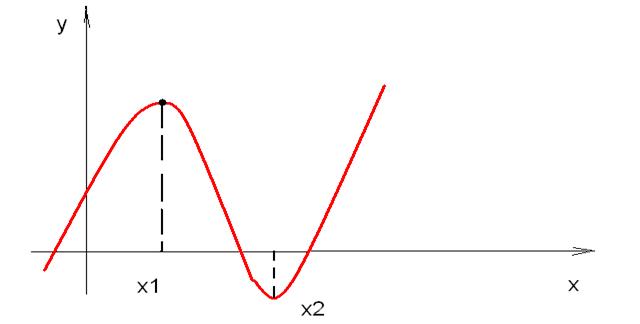
Рисунок 2.

Видим, что при х = х1 и при х = х2 производная равна нулю, у' = 0.

Такие точки называются ЭКСТРЕМУМАМИ.

В промежутке х1< х < х2 функция МОНОТОННО УБЫВАЕТ, здесь у' < 0 – производная отрицательна.

При х > х2 функция МОНОТОННО ВОЗРАСТАЕТ, здесь у '> 0 – производная положительна.

Таким образом, по величине и знаку производной можно судить о характере изменения функции:

у' = 0 – возможен экстремум,

у '> 0 – функция возрастает,

у' < 0 – функция убывает.

Таблица производных и дифференциалов.

Функция	Производная	Дифференциал
Степенная функция
у = С = const	у'= ( C)' = 0	d(C) = 0
у = x	у'= (x)' = 1	d(x) = 1· dx = dx
y = хp	у'=( хp )' = pхp-1	d(xp) = pхp-1dx
у = 1 / м x	у'= -1 / x²	d(1\х) = -1 · dx = -dx j x2 x2 x2
у=(kx+b)р	у'= kр(kx+b)рˉ¹	d((kx+b)р) = kр(kx+b)рˉ¹ dx
y=√x	у'= 1 / 2√х	d(√x) = dx h j 2√х
Показательная функция
y = ах	y'= ахℓnх	d(ах) = ахℓnх dx
y = ℮ˣ	y'= ℮ˣ	d(℮ˣ)=℮ˣdx
y = ℮-ˣ	y'= - ℮-ˣ	d(℮-ˣ)= -℮-ˣdx
y = ℮px	y'= p ℮px	d(℮px)= p ℮px dx
Логарифмическая функция
y=lnx	y'= 1 / x	d(lnx) = dx h x
y = logаx	y' = 1 \ x ln а	d(logаx) = dx \ x ln а
Тригонометрические функции
y = sin x	y'= cos x	d(sin x) = cosx dx
y = cos x	y'= -sin x	d(cos x) = -sinx dx
y = tg x	y' = 1 \ cos²x	d(tg x) = dx \ cos²x
y = ctg x	y'= -1 \ sin²x	d(ctg x) = - dx \ sin²x
Обратные тригонометрические функции
y = arcsinx	y'= 1 / √1-x²	d(arcsinx) = dx и √1-x²
y = arccosx	y'= - 1 / √1-x²	d(arccosx) = - dx / √1-x²
y = arctg x	y'= 1 / 1+x²	d(arctg x) == dx / 1+x²
y = arcctg x	y'= - 1 / 1+x²	d(arcctg x) == - dx / 1+x²
Гиперболические функции
y = sh x	y' = ch x	d(sh x) = ch x dx
y = ch x	y' = sh x	d(ch x) = sh x dx
y = th x	y' = 1 b ch2 x	d(th x) = dx b ch2 x
y = cth x	y' = -1 v sh2 x	d(cth x) = -dx v sh2 x
Обратные гиперболические функции
y = arcsh x	y' = 1 b √1 + x2	d(arcsh x) = dx b √1 + x2
y = arcch x	y' = 1 b √x2 - 1	d(arcch x) = dx b √x2 - 1
y = arcth x	y' = 1 k 1 – x2	d(arcth x) = dx k 1 – x2
y = arccth x	y' = 1 b x2 - 1	d(arccth x) = dx b x2 - 1