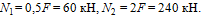Статически неопределимые системы

Брусья и шарнирно-стержневые системы, в которых внутренние усилия невозможно определить с помощью одних лишь уравнений равновесия, называют статически неопределимыми. Такие системы должны быть геометрически неизменяемыми.

Разность между числом неизвестных и числом независимых уравнений равновесия, которые можно составить для данной системы, называют степенью статической неопределимости.

Все статически неопределимые системы имеют «лишние» связи в виде закреплений, стержней или других элементов. Статически неопределимые системы приведены на рис. 4.9, б, в. Степень статической неопределимости определяется по формуле

n = k – 3,

где n – степень статической неопределимости;

k – число неизвестных;

3 – число уравнений статики.

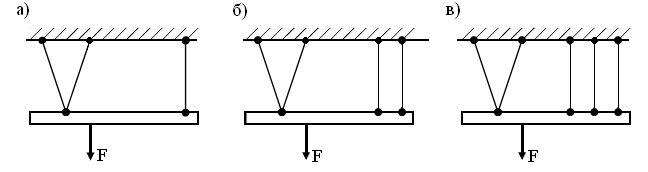
Рис. 4.9. а – статически определимая система; б – 1 раз статически неопределимая

система; в – 2 раза статически неопределимая система

Для раскрытия статической неопределимости необходимо составить дополнительные уравнения, учитывающие деформации элементов системы и перемещения узлов. Такие уравнения называются уравнениями совместности деформаций.

Рассмотрим общие рекомендации и приемы для решения статически неопределимых задач при растяжении (сжатии).

1. Статическая сторона задачи:

- для отсеченных элементов конструкции, содержащих неизвестные усилия, составляются уравнения статики;

- определяется степень статической неопределимости системы.

2. Геометрическая сторона задачи:

- рассматриваем систему в деформированном состоянии и устанавливаем связи между деформациями и перемещениями отдельных элементов конструкции;

- составляем уравнения совместности деформаций.

3. Физическая сторона задачи:

- на основании закона Гука определяем перемещения (деформации) элементов конструкции через действующие в них неизвестные усилия. При изменении температуры к деформациям, вызванным усилиями, добавляются температурные деформации;

- при решении системы уравнений (статических и физических) определяются неизвестные усилия.

Рассмотрим рис. 4.10, а. Так как система симметрична, то N₁=N₂.

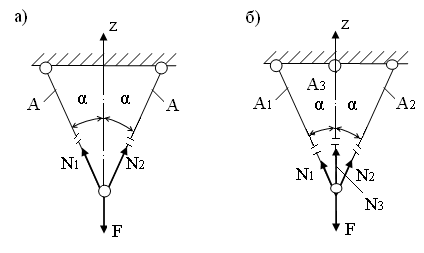
Рис. 4.10. а – статически определимая система;

б – 1 раз статически неопределимая система

Составим уравнение равновесия:

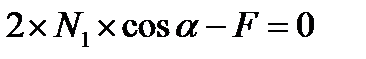, отсюда .

Рассмотрим рис. 4.10, б. Пусть А₁ = А₂, отсюда .

Составим уравнение равновесия:

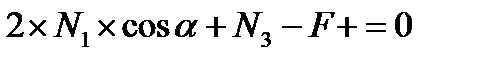, откуда .

Для определения лишнего неизвестного составим уравнение совместности деформаций. Для этого рассмотрим перемещение узла С в результате деформации стержней (рис. 4.10, в).

СС₁ = ∆l₃ – перемещение узла С и удлинение стержня 3;

СС₂ = ∆l₁ – удлинение стержней 1 и 2.

В силу малости деформаций считаем, что угол между стержнями до и после деформации не изменяется, и пренебрегаем величинами второго порядка малости. Используя закон Гука, имеем:

; .

Приравняем эти два выражения, получим:

.

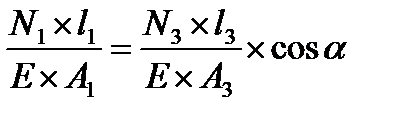Далее из системы уравнений

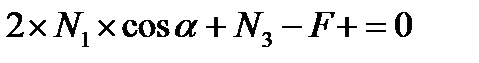
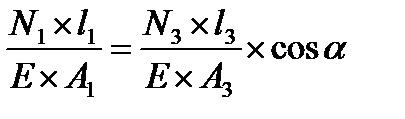
находим N₁, N₂, N₃.

Рассмотрим рис. 4.11, а.

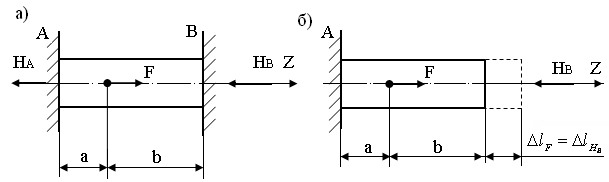
Рис. 4.11. а – схема деформации стержня, защемленного между двумя заделками;

б – расчетная схема стержня для составления уравнения совместности деформаций

1. Составим уравнение равновесия:

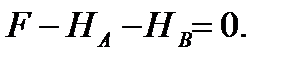
2. Отбросим правую заделку и составим уравнение совместности деформаций. При этом перемещения, вызванные внешней силой F и опорной реакцией H_B, будут одинаковы, т. е. 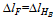, или

,

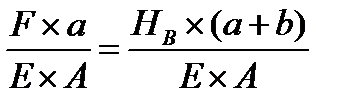где А – площадь поперечного сечения стержня.

3. Решая систему уравнений

,

находим опорные реакции H_A и H_B.

Задача 4. Определить опасное сечение для стержня, изображенного на рис. 4.12, а.

Рис. 4.12. а – схема деформации стержня, защемленного между двумя заделками;

б – эпюра нормальных сил; в – эпюра нормальных напряжений

Решение.

1. Из уравнения совместности деформаций 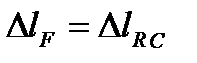имеем:

,

отсюда

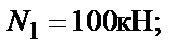
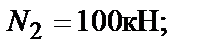
2. Методом сечений определим значения нормальных сил на участках стержня: Эпюра нормальных сил показана на рис. 4.12, б.

3. Определим значения нормальных напряжений на участках стержня:

; ;

.

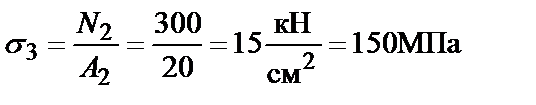Эпюра нормальных напряжений изображена на рис. 4.12, в.

4. Опасное сечение стержня находится на 3-м участке.

Задача 5.Невесомый брус подвешен на двух стержнях длиной l₁ = = 2 м, l₂ = 1 м. На конце бруса приложена внешняя сила F = 120 кН (рис. 4.13, а). Площадь поперечного сечения стержня 1 А = 10 см². Е₁ = = Е₂ = 2´10⁴ . Определить значения нормальных сил N₁, N₂.

Рис. 4.13. а, б – расчетная схема бруса; в – расчетная схема для определения абсолютных деформаций стержней 1 и 2

Решение.

Проведем сечения в стержнях 1 и 2 (рис. 4.13, а). Составим уравне-ние равновесия отсеченной части:

.

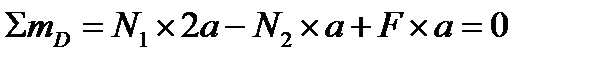2. Расчетная схема деформации стержней под действием внешней нагрузки показана на рис. 4.13, в. Из подобия имеем:

.

Согласно закону Гука данное выражение представим в виде:

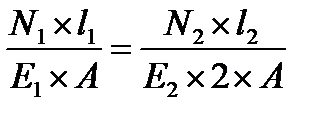, откуда 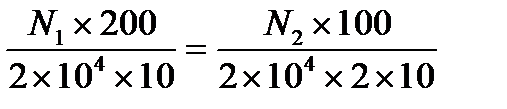, или .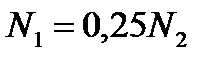

3. Решая систему уравнений

;

,

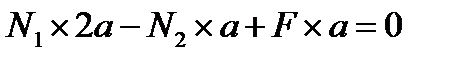находим