Непрерывность основных элементарных функций.

Сформулируем теоремы о непрерывности функций, полученных в результате арифметических действий над непрерывными функциями, а также их композиции.

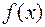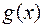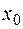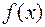
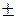
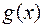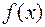
Доказательства этих теорем однотипны и основываются на опре­делении непрерывности функции в точке. Теорема. Если функции и непрерывны в точке , то и функции , 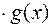непрерывны в точке 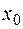. Если, кроме того, 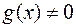, то функция 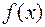/ 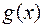является также непрерывной в точке 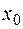. Доказательство. Докажем, например, непрерывность функции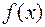 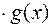в точке 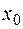. Из непрерывности функци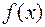й и 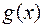в точке 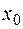следует, что 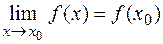, 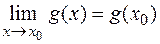. Тогда

.

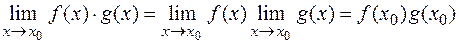т. е. функция 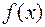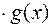непрерывна в точке 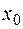. Аналогично доказы­ваются другие утверждения теоремы. Эту теорему можно обобщить на случай конечного числа функ­ций: алгебраическая сумма и произведение конечного числа функций, непрерывных в точке х₀, непрерывны в точке .

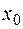Сформулируем теорему о непрерывности сложной функции. Теорема. Сложная функция, являющаяся композицией ко­нечного числа непрерывных в точке 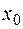функций, непрерывна в точке .

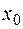Доказательство. Докажем эту теорему для случая, когда сложная функция является композицией двух непрерывных в точке 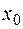функци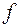й и .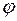

Пусть 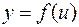, , 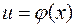тогда по определению сложной функции

.

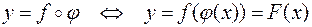Теорема утверждает, что если функция 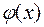непрерывна в точке 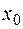, а функция 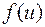непрерывна в точке 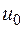, то сложная функция 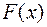непрерывна в точке .

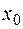Действительно, пусть 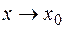. Тогда из непрерывности функции 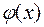следует, что 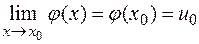, т. е. что 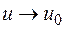. Поскольку

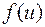непрерывна в точке 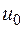, то 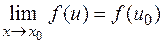Но так как 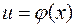, то последнее равенство можно записать в виде 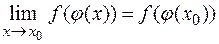или 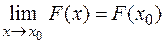Из определения 1 непрерывной функции в точке 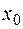и последней теоремы следует, что 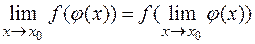или в частном случае

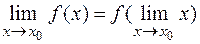т. е. символы предела и непрерывной функции перестановочны. Приведем без доказательства следующие две теоремы.

Теорема. Пусть функция 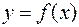определена, непрерывна и монотонна на некотором множестве X и пусть Y — множество ее значений. Тогда на множестве Y обратная функция 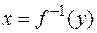моно­тонна и непрерывна. Теорема. Основные элементарные функции непрерывны во всех точках, принадлежащих их области определения.

21. Понятие производной функции одной переменной. Геометрический и физический смысл производной.

Производной функции f (x) в точке х0 называется предел (если он существует) отношения приращения функции в точке х0 к приращению аргумента Δх, если прирост аргумента стремится к нулю и обозначается f ‘(x0). Действие нахождения производной функции называется дифференцированием.
Производная функции имеет такой физический смысл: производная функции в заданной точке — скорость изменения функции в заданной точке.

Геометрический смысл производной. Производная в точке x0 равна угловому коэффициенту касательной к графику функции y=f(x) в этой точке.

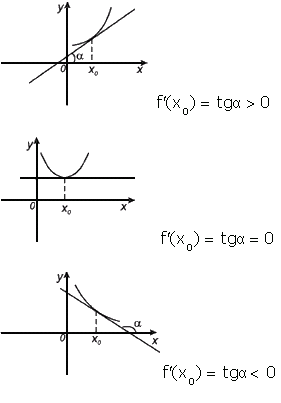
Физический смысл производной.Если точка движется вдоль оси х и ее координата изменяется по закону x(t), то мгновенная скорость точки:

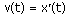
Рассмотрим движение точки по прямой. Пусть задана координата точки в любой момент времени x(t). Известно (из курса физики), что средняя скорость за промежуток времени [t₀; t₀+ ∆t] равна отношению расстояния, пройденного за этот промежуток времени, на время, т.е.

Vср = ∆x/∆t. Перейдем к пределу в последнем равенстве при ∆t → 0.

(tnlim Vср (t) = ₀) - мгновенная скорость в момент времени t₀, ∆t → 0.

а lim = ∆x/∆t = x'(t₀) (по определению производной).

(t) =x'(t).nИтак,

Физический смысл производной заключается в следующем: произ­водная функции y = f(x) в точке x₀ - это скорость изменения функции f (х) в точке x₀

Производная применяется в физике для нахождения скорости по известной функции координаты от времени, ускорения по известной функции скорости от времени.

(t) = x'(t) - скорость,u

'(t) - ускорение, илиna(f) = a(t) = x"(t). Если известен закон движения материальной точки по окружности, то можно найти угловую скорость и угловое ускорение при вращатель­ном движении:

φ = φ(t) - изменение угла от времени, ω = φ'(t) - угловая скорость, ε = φ'(t) - угловое ускорение, или ε = φ"(t).

Если известен закон распределения массы неоднородного стержня, то можно найти линейную плотность неоднородного стержня:

m = m(х) - масса, [0; l], l - длина стержня,Îx р = m'(х) - линейная плотность.

С помощью производной решаются задачи из теории упругости и гармонических колебаний. Так, по закону Гука F = -kx, x – переменная координата, k- коэффициент упругости пружины. Положив ω² =k/m, получим дифференциальное уравнение пружинного маятника х"(t) + ω²x(t) = 0,

где ω = √k/√m частота колебаний (l/c), k - жесткость пружины (H/m).

Уравнение вида у" + ω²y = 0 называется уравнением гармонических колебаний (механических, электрических, электромагнитных). Решени­ем таких уравнений является функция у = Asin(ωt + φ₀) или у = Acos(ωt + φ₀), где

А - амплитуда колебаний, ω - циклическая частота, φ₀ - начальная фаза.