Сходящаяся и расходящаяся последовательность. Свойства сходящихся последовательностей. В тетр

Сходящиеся и расходящиеся последовательности

• Сходящаяся последовательность — это последовательность элементов множества 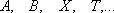, имеющая предел в этом множестве.
• Расходящаяся последовательность — это последовательность, не являющаяся сходящейся.

Свойства сходящихся последовательностей

• Всякая бесконечно малая последовательность является сходящейся. Её предел равен нулю.
• Удаление любого конечного числа элементов из бесконечной последовательности не влияет ни на сходимость, ни на предел этой последовательности.
• Любая сходящаяся последовательность элементов хаусдорфова пространства имеет только один предел.
• Любая сходящаяся последовательность ограничена. Однако не любая ограниченная последовательность сходится.
• Последовательность сходится тогда и только тогда, когда она является ограниченной и при этом её верхний и нижний пределы совпадают.
• Если последовательность 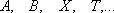сходится, но не является бесконечно малой, то, начиная с некоторого номера, определена последовательность 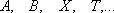, которая является ограниченной.
• Сумма сходящихся последовательностей также является сходящейся последовательностью.
• Разность сходящихся последовательностей также является сходящейся последовательностью.
• Произведение сходящихся последовательностей также является сходящейся последовательностью.
• Частное двух сходящихся последовательностей определено, начиная с некоторого элемента, если только вторая последовательность не является бесконечно малой. Если частное двух сходящихся последовательностей определено, то оно представляет собой сходящуюся последовательность.
• Если сходящаяся последовательность ограничена снизу, то никакая из её нижних граней не превышает её предела.
• Если сходящаяся последовательность ограничена сверху, то её предел не превышает ни одной из её верхних граней.
• Если для любого номера члены одной сходящейся последовательности не превышают членов другой сходящейся последовательности, то и предел первой последовательности также не превышает предела второй.
• Если все элементы некоторой последовательности, начиная с некоторого номера, лежат на отрезке между соответствующими элементами двух других сходящихся к одному и тому же пределу последовательностей, то и эта последовательность также сходится к такому же пределу.
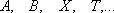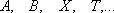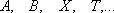• Любую сходящуюся последовательность можно представить в виде , где — предел последовательности 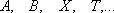, а 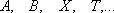— некоторая бесконечно малая последовательность.
• Всякая сходящаяся последовательность является фундаментальной. При этом фундаментальная числовая последовательность всегда сходится (как и любая фундаментальная последовательность элементов полного пространства).

11. Предел функции одной переменной. Односторонние пределы функции.в тетр

В определении предела функции считается, что х стремится к х₀ любым способом: оставаясь меньшим, чем х₀ (слева от х₀), большим, чем х₀ (справа от х₀), или колеблясь около точки х₀. Бывают случаи, когда способ приближения аргумента х к х₀ существенно влияет на значение предела функции.

Число А₁ называется пределом функции 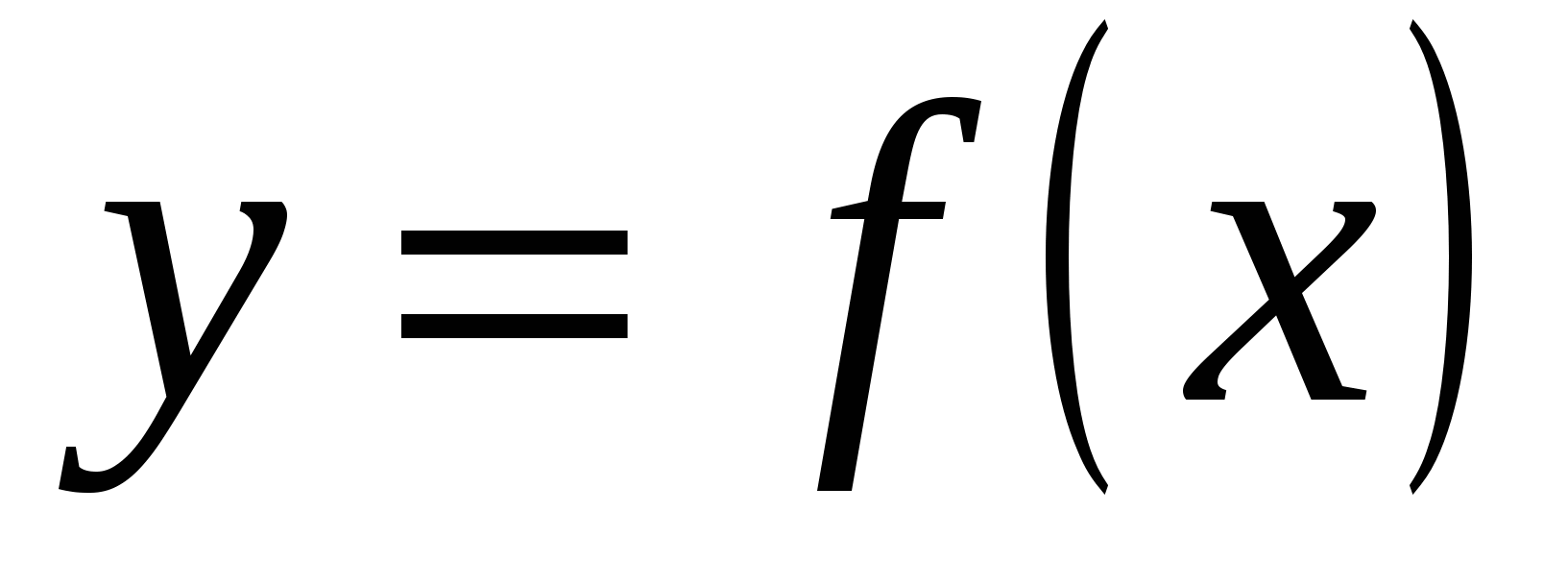в точке х₀ слева, если

.

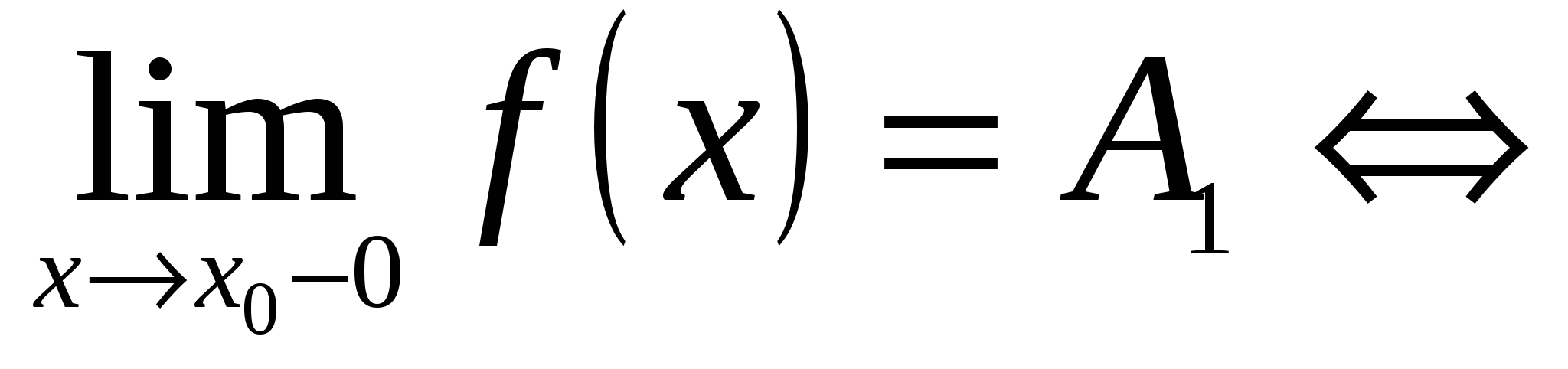
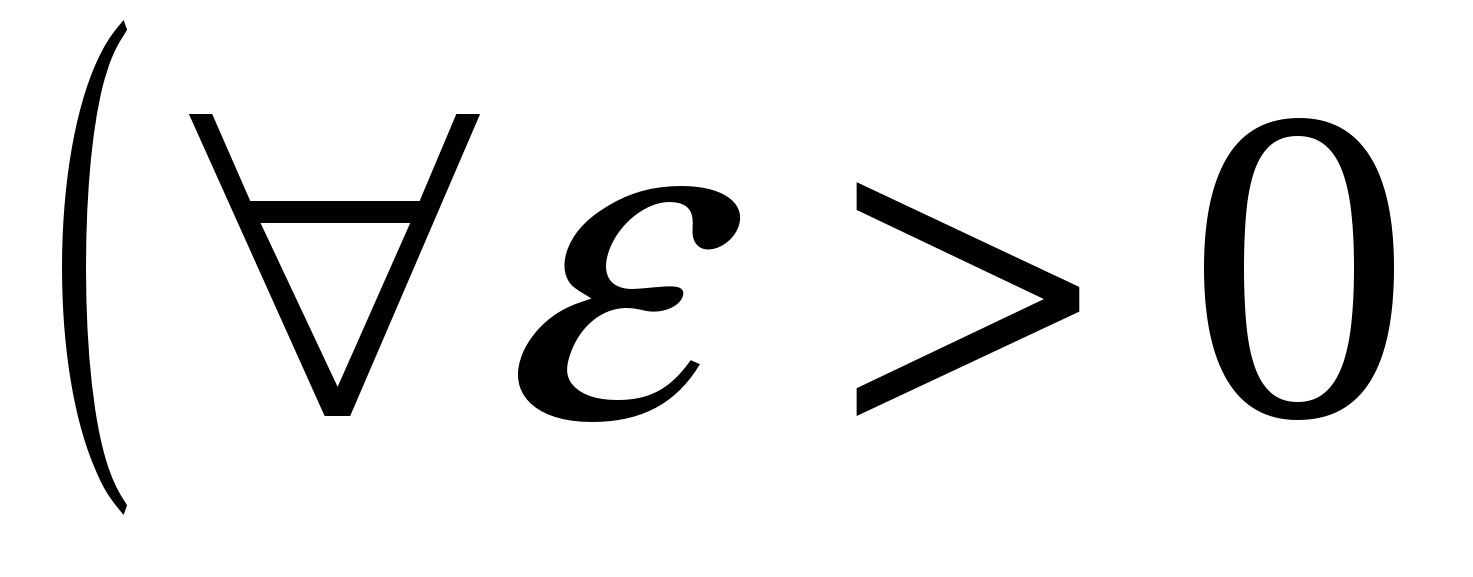
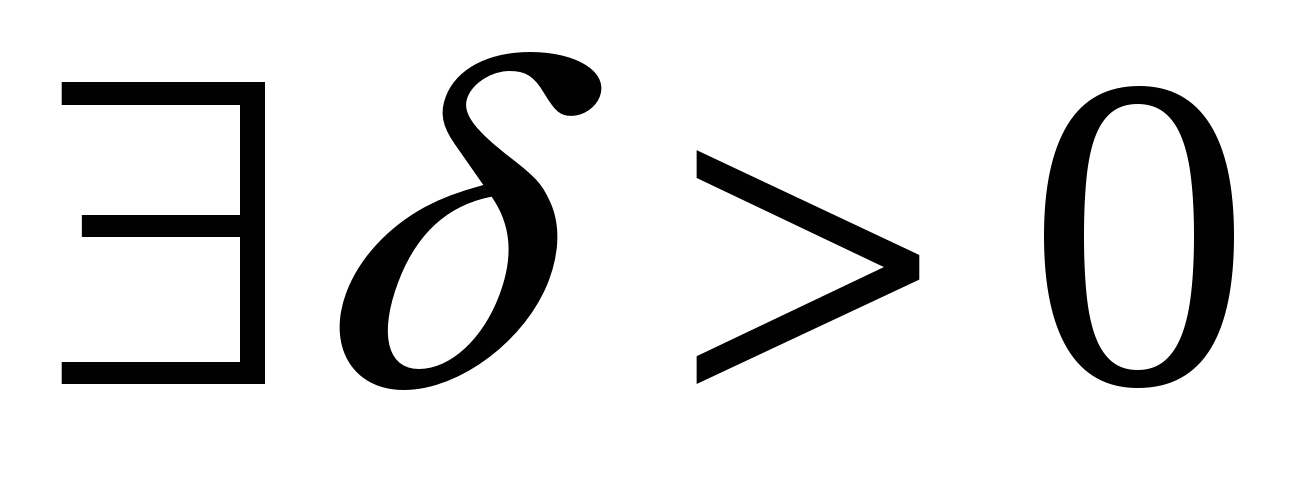
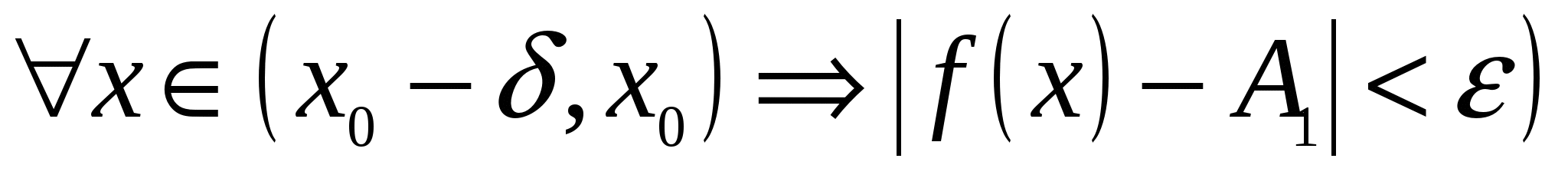Аналогично определяется предел функции справа:

.

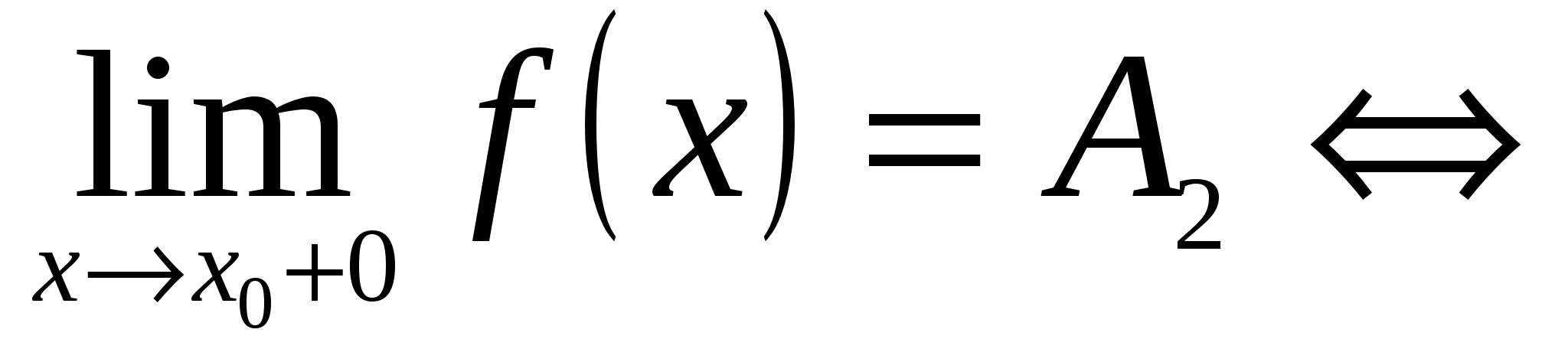
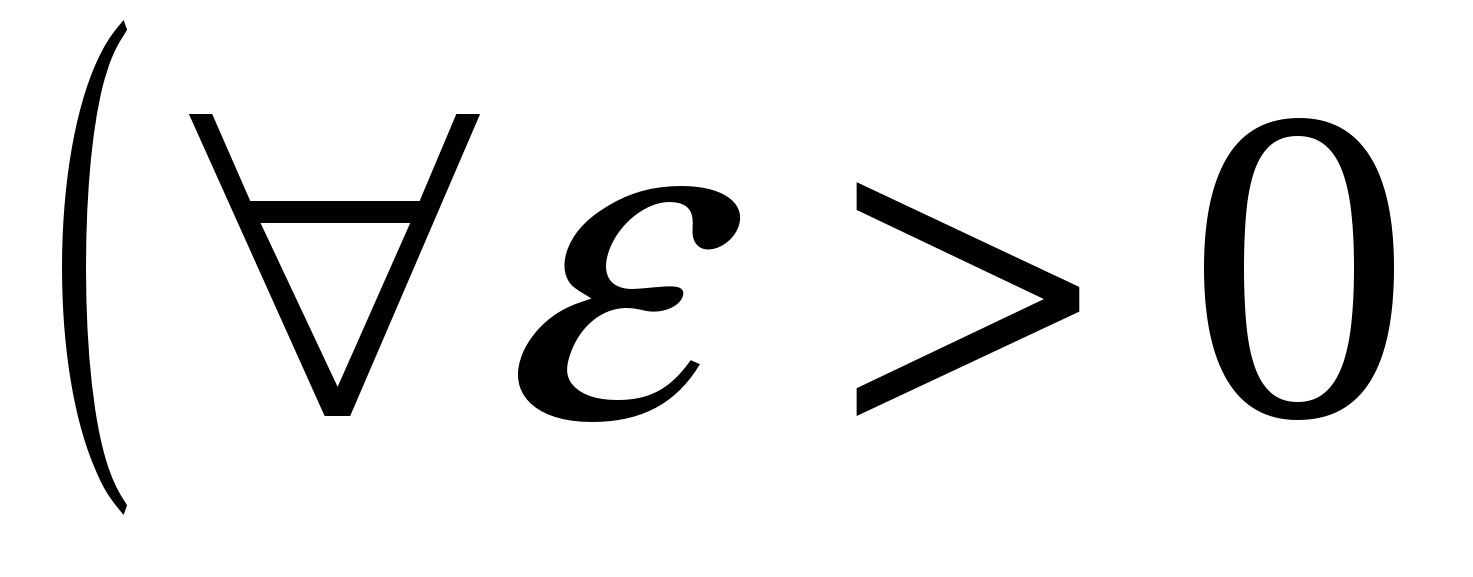
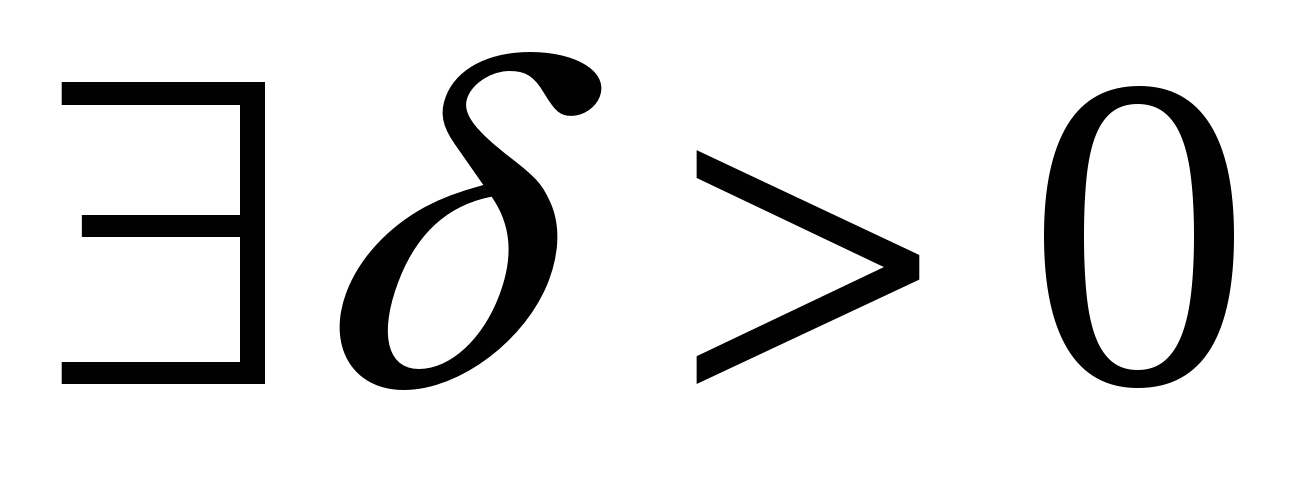
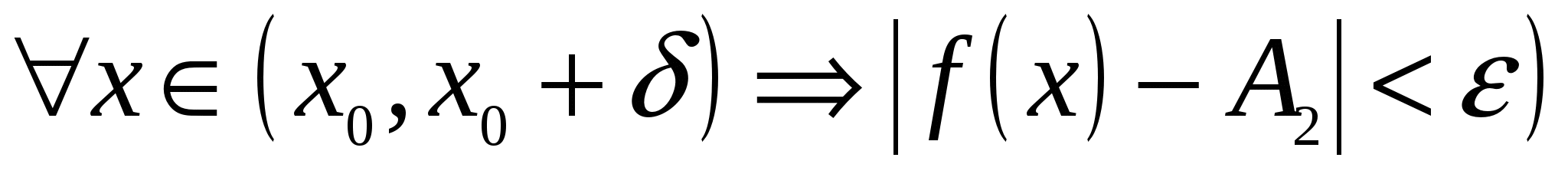Пределы функции справа и слева называются односторонними пределами. Очевидно, что если существует 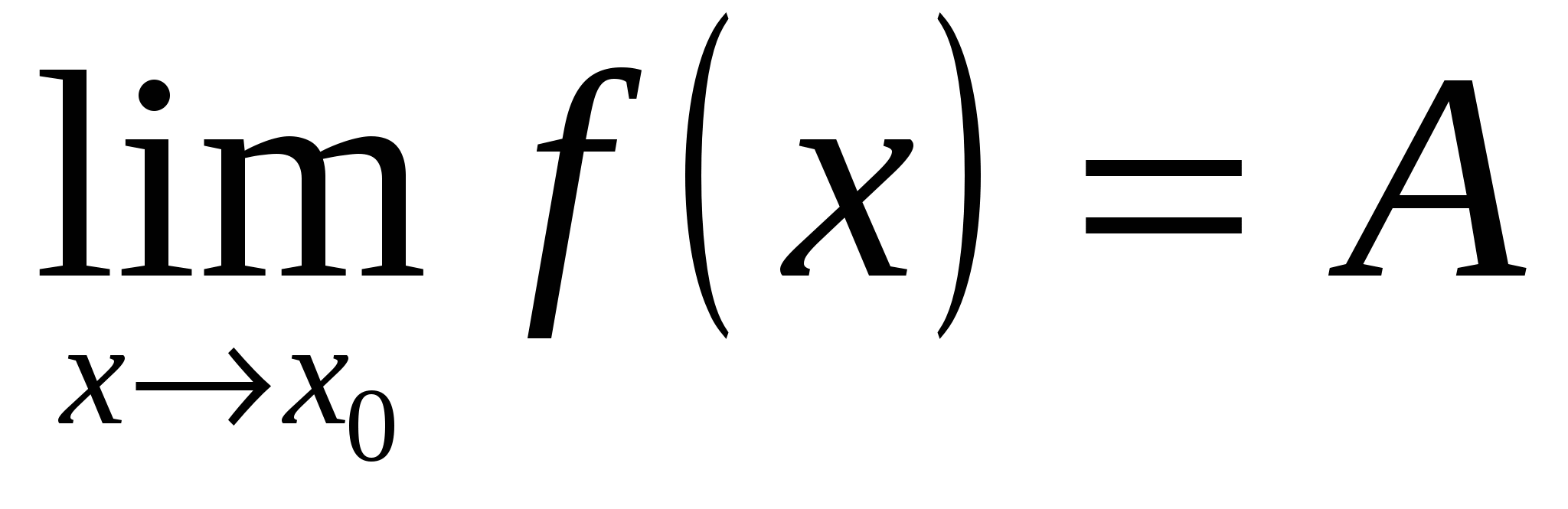, то существуют и оба односторонних предела. Справедливо и обратное: если существую оба односторонних предела и они равны, то существует

.

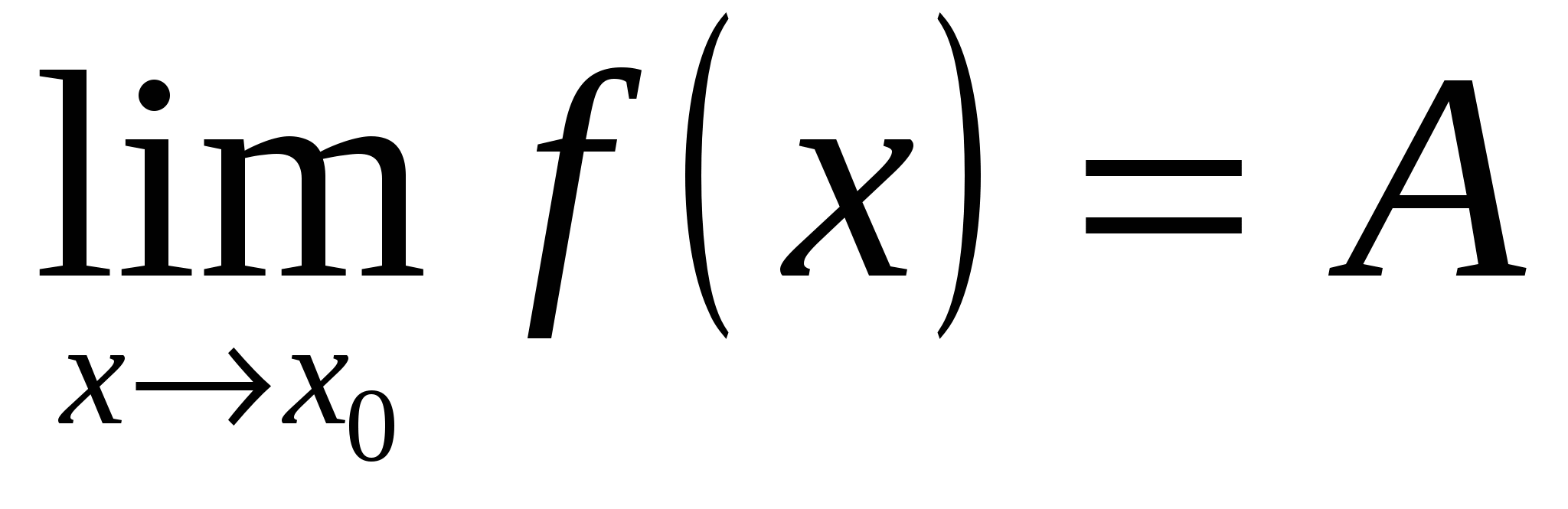
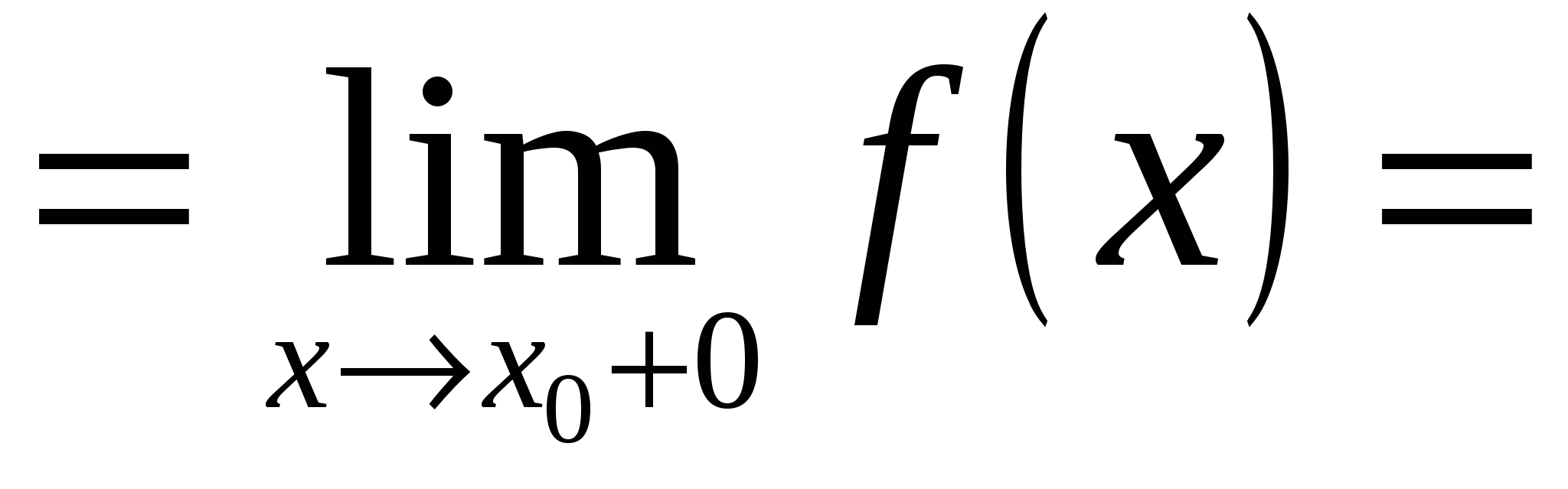
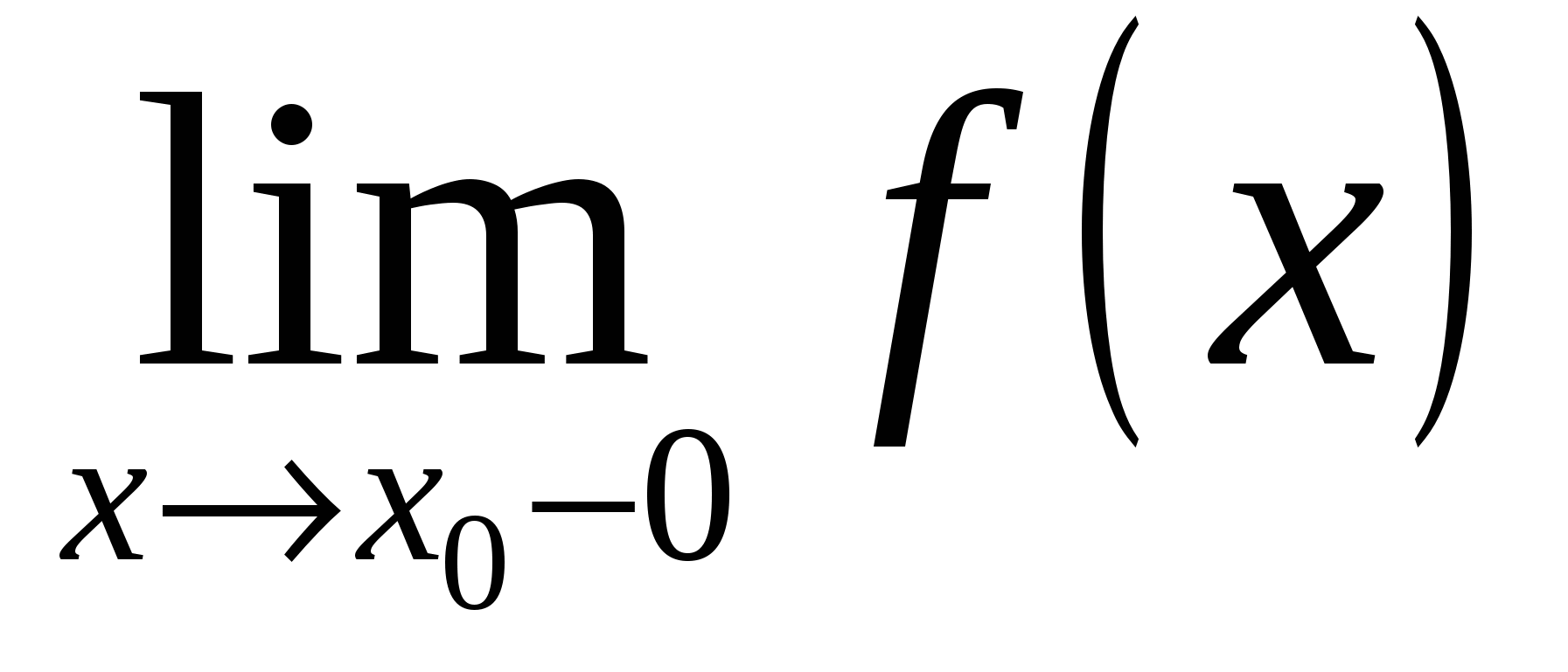Если же 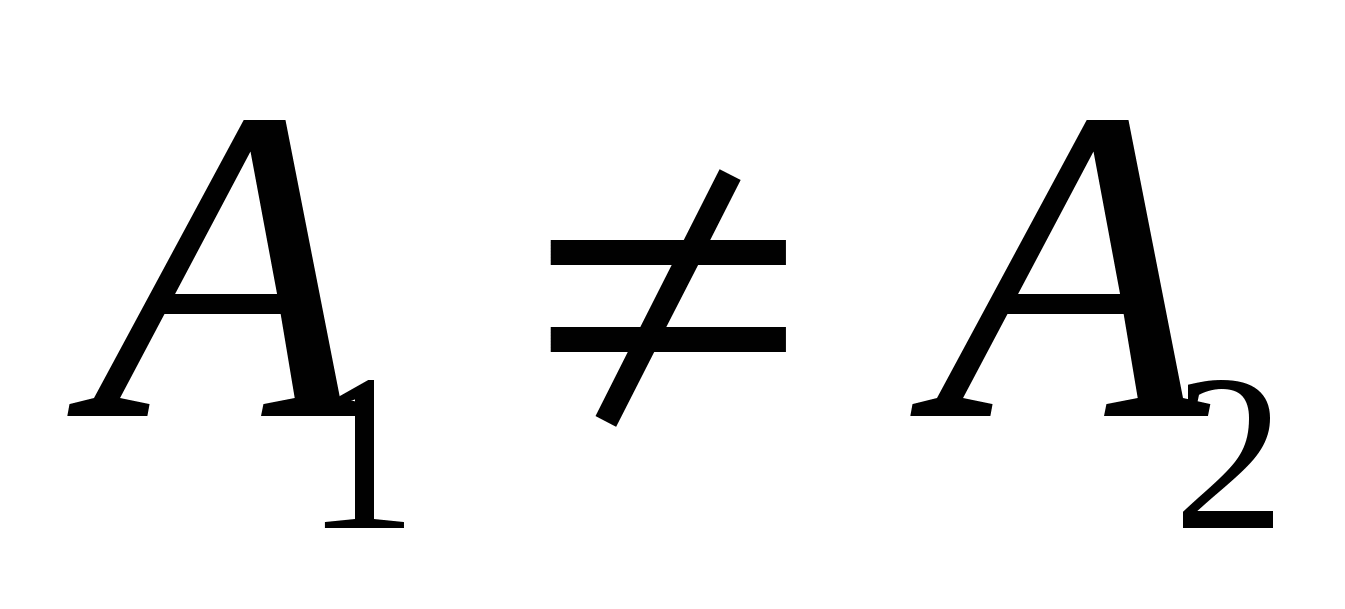, то 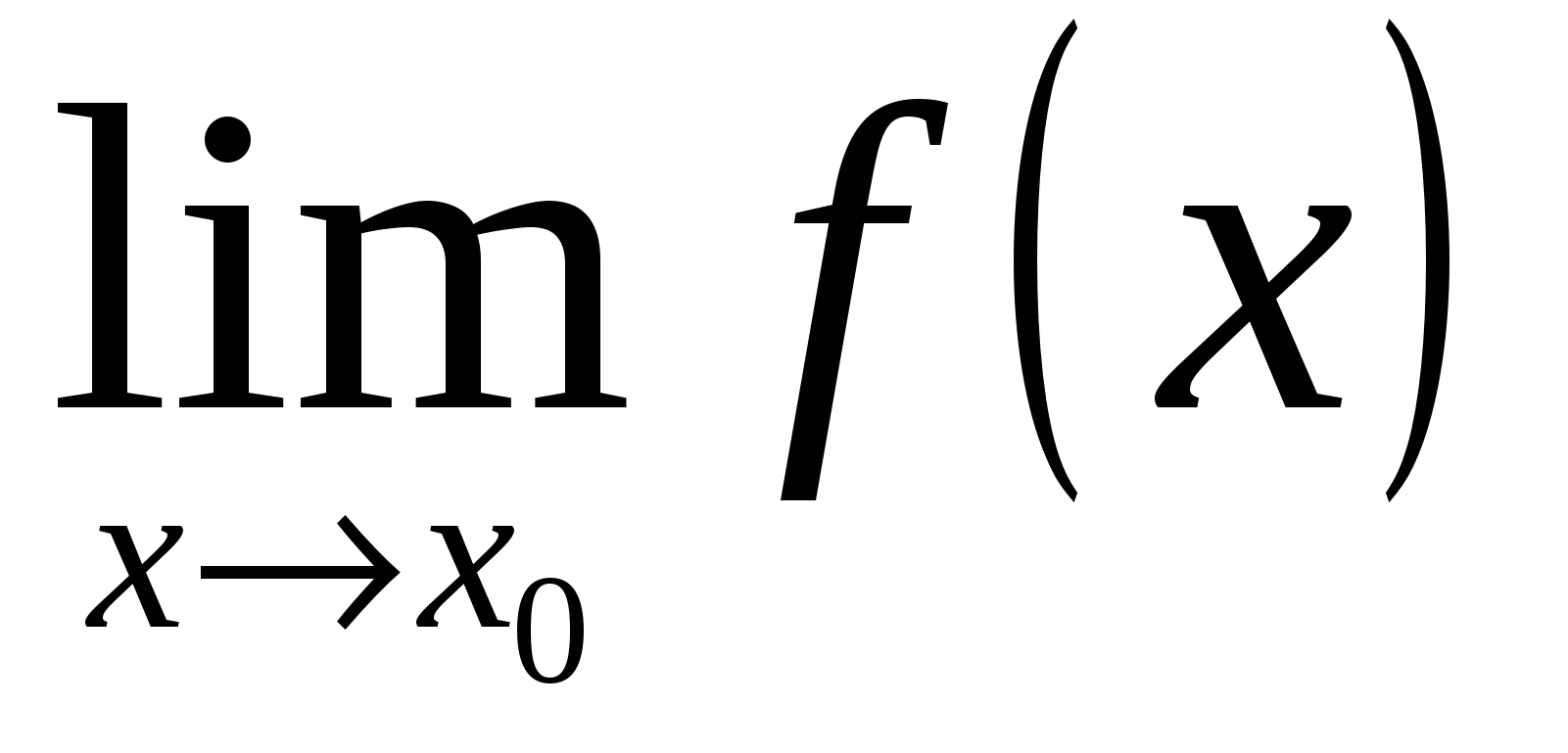не существует.

12. Бесконечно малые (бесконечно большие) величины; их свойства. В тетр

13. Связь бесконечно малых величин с пределом функции.

Если функция 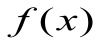имеет при 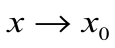( 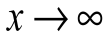) предел, равный 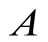, то ее можно представить в виде суммы этого числа 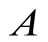и бесконечно мало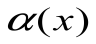й при 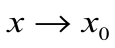( 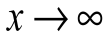), т.е. 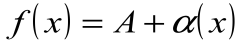. Теорема 2. Если функцию 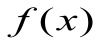можно представить как сумму числа 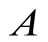и бесконечно мало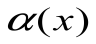й при 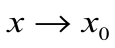( 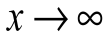), то число 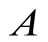есть предел этой функции при 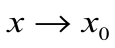( 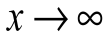), т.е. .

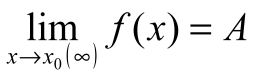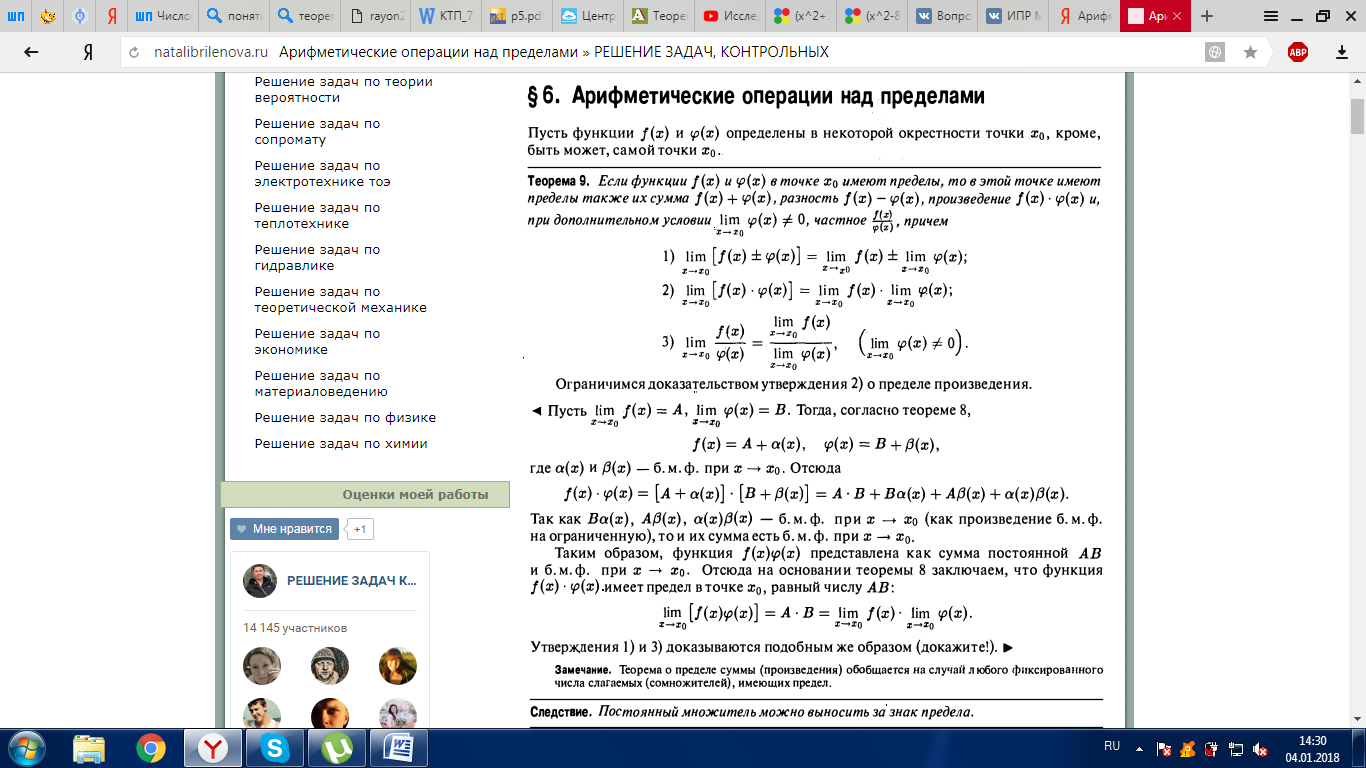
14. Арифметические операции над пределами функций.

15. Замечательные пределы. В тетр

Первый замечательный предел

Рассмотрим следующий предел: 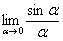(вместо родной буквы «хэ» я буду использовать греческую букву «альфа», это удобнее с точки зрения подачи материала).

Согласно нашему правилу нахождения пределов пробуем подставить ноль в функцию: в числителе у нас получается ноль (синус нуля равен нулю), в знаменателе, очевидно, тоже ноль. Таким образом, мы сталкиваемся с неопределенностью вида 0/0 , которую, к счастью, раскрывать не нужно. В курсе математического анализа, доказывается, что:

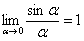
Данный математический факт носит название Первого замечательного предела. Нередко в практических заданиях функции могут быть расположены по-другому, это ничего не меняет:

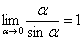– тот же самый первый замечательный предел.

! Но самостоятельно переставлять числитель и знаменатель нельзя! Если дан предел в виде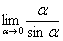, то и решать его нужно в таком же виде, ничего не переставляя.

На практике в качестве параметра 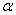может выступать не только переменная 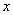, но и элементарная функция, сложная функция. Важно лишь, чтобы она стремилась к нулю.

Примеры:
, , ,

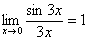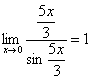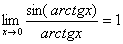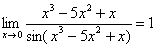
Здесь 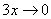, , 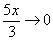, , 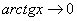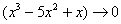и всё гуд – первый замечательный предел применим.

А вот следующая запись – ересь:

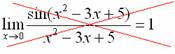
Почему? Потому что многочлен 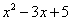не стремится к нулю, он стремится к пятерке.

Кстати, вопрос на засыпку, а чему равен предел 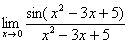? Ответ можно найти.

Переходим к рассмотрению практических примеров:

Пример 1

Найти предел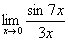

Если мы замечаем в пределе синус, то это нас сразу должно наталкивать на мысль о возможности применения первого замечательного предела.

Сначала пробуем подставить 0 в выражение под знак предела (делаем это мысленно или на черновике):

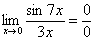Итак, у нас есть неопределенность вида 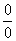, ее обязательно указываем в оформлении решения. Выражение под знаком предела у нас похоже на первый замечательный предел, но это не совсем он, под синусом находится 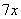, а в знаменателе .

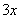В подобных случаях первый замечательный предел нам нужно организовать самостоятельно, используя искусственный прием. Ход рассуждений может быть таким: «под синусом у нас 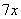, значит, в знаменателе нам тоже нужно получить ».

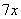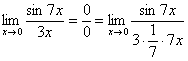
То есть, знаменатель искусственно умножается в данном случае на 7 и делится на ту же семерку. Теперь запись у нас приняла знакомые очертания.
Когда задание оформляется от руки, то первый замечательный предел желательно пометить простым карандашом:

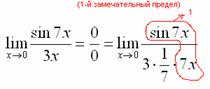
Что произошло? По сути, обведенное выражение у нас превратилось в единицу и исчезло в произведении:

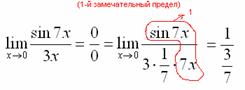
Теперь только осталось избавиться от трехэтажности дроби:
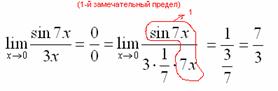Готово. Окончательный ответ: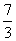

Если не хочется использовать пометки карандашом, то решение можно оформить так:

“

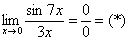
Используем первый замечательный предел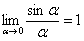

“

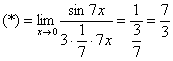
Пример 2

Найти предел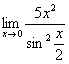

Опять мы видим в пределе дробь и синус. Пробуем подставить в числитель и знаменатель ноль:
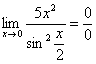Действительно, у нас неопределенность 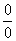и, значит, нужно попытаться организовать первый замечательный предел. что когда у нас есть неопределенность 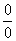, то нужно разложить числитель и знаменатель на множители. Здесь – то же самое, степени мы представим в виде произведения (множителей):

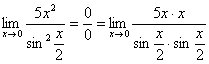
Далее, по уже знакомой схеме организовываем первые замечательные пределы. Под синусами у нас 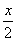, значит, в числителе тоже нужно получить :

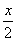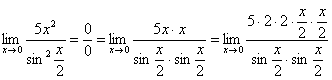
Аналогично предыдущему примеру, обводим карандашом замечательные пределы (здесь их два), и указываем, что они стремятся к единице:

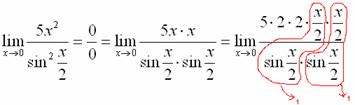
Собственно, ответ готов:

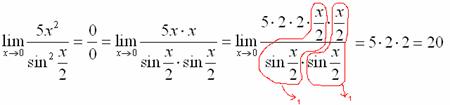
В следующих примерах, я не буду заниматься художествами в Пэйнте, думаю, как правильно оформлять решение в тетради – Вам уже понятно.

Пример 3

Найти предел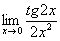

Подставляем ноль в выражение под знаком предела:

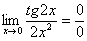
Получена неопределенность 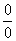, которую нужно раскрывать. Если в пределе есть тангенс, то почти всегда его превращают в синус и косинус по известной тригонометрической формуле 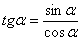(кстати, с котангенсом делают примерно то же самое, см. методический материал ). В данном случае:

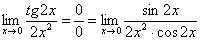Косинус нуля равен единице, и от него легко избавиться (не забываем пометить, что он стремится к единице):

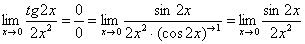Таким образом, если в пределе косинус является МНОЖИТЕЛЕМ, то его, грубо говоря, нужно превратить в единицу, которая исчезает в произведении.

Дальше по накатанной схеме, организуем первый замечательный предел:

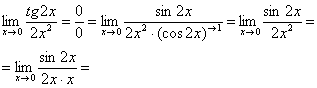
Здесь все вышло проще, без всяких домножений и делений. Первый замечательный предел тоже превращается в единицу и исчезает в произведении:

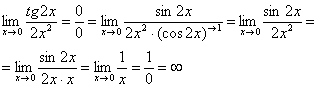
В итоге получена бесконечность, бывает и такое.

Пример 4

Найти предел 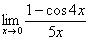Пробуем подставить ноль в числитель и знаменатель:

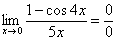
Получена неопределенность 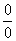(косинус нуля, как мы помним, равен единице)

Используем тригонометрическую формулу 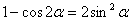. Возьмите на заметку! Пределы с применением этой формулы почему-то встречаются очень часто.

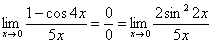Постоянные множители вынесем за значок предела:

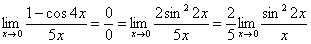Организуем первый замечательный предел:

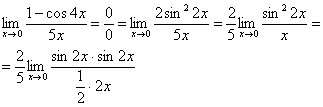
Здесь у нас только один замечательный предел, который превращается в единицу и исчезает в произведении:

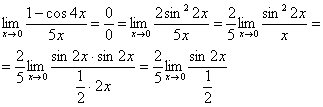Избавимся от трехэтажности:

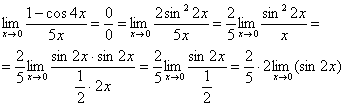
Предел фактически решен, указываем, что оставшийся синус стремится к нулю:

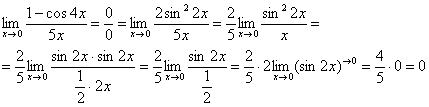
Пример 5

Найти предел 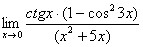Этот пример сложнее, попробуйте разобраться самостоятельно:

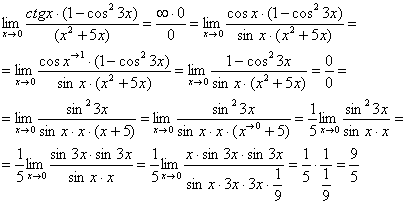
Некоторые пределы можно свести к 1-му замечательному пределу путём замены переменно

Второй замечательный предел

В теории математического анализа доказано, что:

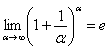
Данный факт носит название второго замечательного предела.

Справка: 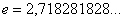– это иррациональное число.

В качестве параметра 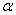может выступать не только переменная 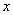, но и сложная функция. Важно лишь, чтобы она стремилась к бесконечности.

Пример 6 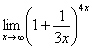Найти предел

Когда выражение под знаком предела находится в степени – это первый признак того, что нужно попытаться применить второй замечательный предел.Но сначала, как всегда, пробуем подставить бесконечно большое число в выражение 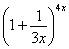Нетрудно заметить, что при основание степени 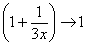, а показатель – 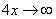, то есть имеется, неопределенность вида :

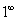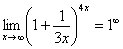Данная неопределенность как раз и раскрывается с помощью второго замечательного предела. Но, как часто бывает, второй замечательный предел не лежит на блюдечке с голубой каемочкой, и его нужно искусственно организовать. Рассуждать можно следующим образом: в данном примере параметр 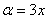, значит, в показателе нам тоже нужно организовать 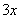. Для этого возводим основание в степень 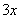, и, чтобы выражение не изменилось – возводим в степень :

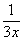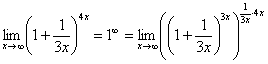
Когда задание оформляется от руки, карандашом помечаем:

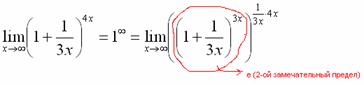
Практически всё готово, страшная степень превратилась в симпатичную букву :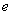

При этом сам значок предела перемещаем в показатель:

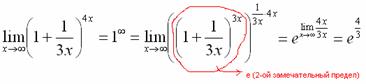
Далее, отметки карандашом я не делаю, принцип оформления, думаю, понятен.

Пример 7

Найти предел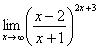

Внимание! Предел подобного типа встречается очень часто, пожалуйста, очень внимательно изучите данный пример.

Пробуем подставить бесконечно большое число в выражение, стоящее под знаком предела:

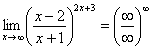
В результате получена неопределенность 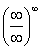. Но второй замечательный предел применим к неопределенности вида 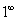. Что делать? Нужно преобразовать основание степени. Рассуждаем так: в знаменателе у нас 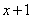, значит, в числителе тоже нужно организовать :

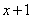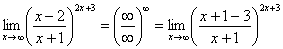
Теперь можно почленно разделить числитель на знаменатель:

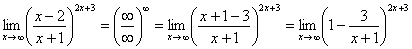
Вроде бы основание стало напоминать 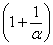, но у нас знак «минус» да и тройка какая-то вместо единицы. Поможет следующее ухищрение, делаем дробь трехэтажной:

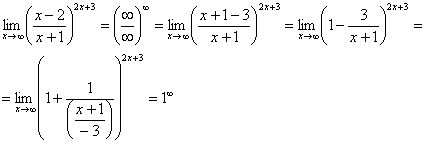
Таким образом, основание приняло вид 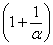, и, более того, появилась нужная нам неопределенность 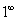. Организуем второй замечательный предел .
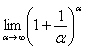Легко заметить, что в данном примере 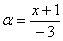. Снова исполняем наш искусственный прием: возводим основание степени в 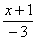, и, чтобы выражение не изменилось – возводим в обратную дробь :

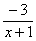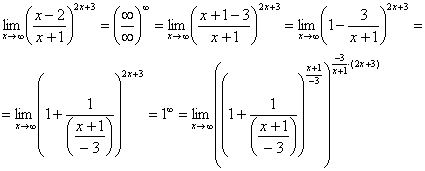
Наконец-то долгожданное 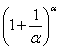устроено, с чистой совестью превращаем его в букву :

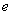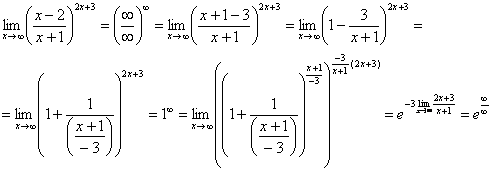
Но на этом мучения не закончены, в показателе у нас появилась неопределенность вида 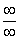, Делим числитель и знаменатель на :

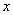Готово.

А сейчас мы рассмотрим модификацию второго замечательного предела. Напомню, что второй замечательный предел выглядит следующим образом: 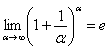. Однако на практике время от времени можно встретить его «перевёртыш», который в общем виде записывается так:

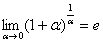
Пример 8

Найти предел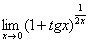

Сначала (мысленно или на черновике) пробуем подставить ноль (бесконечно малое число) в выражение, стоящее под знаком предела:

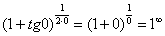
В результате получена знакомая неопределенность 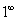. Очевидно, что в данном примере 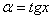. С помощью знакомого искусственного приема организуем в показателе степени конструкцию :

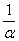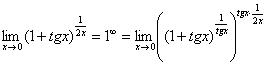
Выражение 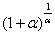со спокойной душой превращаем в букву :

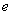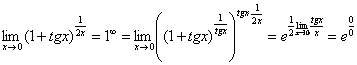
Еще не всё, в показателе у нас появилась неопределенность вида 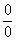. Раскладываем тангенс на синус и косинус (ничего не напоминает?):

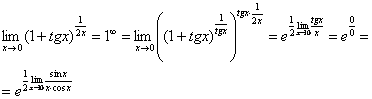
Косинус нуля стремится к единице (не забываем помечать карандашом), поэтому он просто пропадает в произведении: