Высказывания и основные операции над ними. Таблицы истинности.

Высказывания и основные операции над ними. Таблицы истинности.

Высказывание – всякое утверждение, о котором объективно и определенно можно сказать, истинно оно или ложно.

· значения истинности высказывания – 1 (истина) и 0 (ложь).

Операции:

• Отрицание. Отрицанием А называется высказывание Ø А («не А»), которое истинно, когда ложно А, и ложно, когда А истинно.

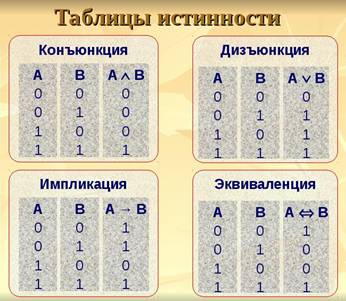
• Конъюнкция. Конъюнкцией (от лат. conjunctio – союз, связь) высказываний А и В называется высказывание А Ù В («А и В»), истинное в том и только в том случае, когда оба высказывания А и В истинны.

• Дизъюнкция. Дизъюнкцией (от лат. disjunctio – различие) высказываний А и В называется высказывание АÚВ («А или В»), ложное в том и только в том случае, когда оба высказывания А и В ложны.

• Импликация.Импликацией (от лат. implico – тесно связаны) высказываний А и В называется высказывание АÞ В («А влечет В», «А имплицирует В», ложное в том и только в том случае, когда А истинно, а В ложно. (если А, то Б)

• Эквиваленция. Эквиваленцией высказываний А и В называется высказывание АÛВ («А эквивалентно В», «эквиваленция А и В», истинное в том и только в том случае, когда высказывания А и В оба истинны или оба ложны.

Эквивалентные высказывания и логические законы.

Формула A (X₁, …, X_n), принимающая для всех значений из Bⁿ значение 1, называется тождественно истинным(ТИ-)высказыванием, а формула, принимающая для всех значений из Bⁿ значение 0 – тождественно ложным (ТЛ-) высказыванием.Тождественно истинные высказывания записывают законы, так как они истинны только в силу своей формы, независимо от содержания исходных высказываний.

3. Одноместные предикаты: основные понятия, использование кванторов общности и существования.

В каждом высказывании есть подлежащее и сказуемое, т.е. объект и предикат (свойство объекта).

Множество объектов, для которых может быть определен данный предикат, образуют поле предиката М.

предикат – это функция Р(х), определенная на М со значениями «истина» или «ложь».

Для того, чтобы характеризовать свойства не каждого отдельного объекта, а всей их совокупности (всего поля предиката), используются кванторы.

квантор общности (обозначается ) и квантор существования (обозначается )

Переход от P(x) к xP(x) называется навешиванием квантора общности по предметной переменной x.

При этом переходе предикату P(x) ставится в соответствие высказывание xP(x) (читается: «для всякого x имеет место P(x)»), которое по определению является истинным тогда и только тогда,

когда высказывание P(a) истинно для любого a M.

Переход от P(x) к xP(x) называется навешиванием квантора существования по предметной переменной x.

При этом переходе предикату P(x) ставится в соответствие высказывание xP(x)

(читается: «существует такое x, что имеет место P(x)»), которое по определению является истинным тогда и только тогда, когда высказывание P(a) истинно хотя бы для одного a M.

4. Двухместные предикаты: основные понятия, использование кванторов общности и существования.

Если в предложении содержится утверждение о нескольких объектах и отношениях между ними, то оно может быть записано с использованием многоместного предиката.

Например, высказывание «3 > 0» («3 больше 0») может быть формализовано не только с помощью одноместного предиката Р(х) («х > 0»), но и двухместного предиката Р(х, у) («х > y»).

Прямое (декартово) произведение множеств.

Бинарные отношения. Графическое представление бинарных отношений.

Виды матриц. Геометрическая интерпретация векторов.

Матрица A размера m´n – таблица чисел, содержащая m строк и n столбцов. (A_mn)

Виды:

· Матрица (вектор)-строка – состоящая из одной строки

· Матрица (вектор) – столбец – состоящая из одного столбца

· Квадратная n-го порядка – чисто строк=числу столбцов

· Диагональная – все недиагональные элементы матрицы = 0

· Единичная – если у диагональной все диагональные элементы = 1

· Нулевая – все элементы равны 0

· Верхней (нижней) треугольной матрицей называется квадратная матрица произвольного порядка, все элементы которой, стоящие под (над) главной диагональю, равны нулю.

Умножение матриц.

Результат умножения матрицы A размера m´k на матрицу B размера k´n – матрица C размера m´n, каждый элемент которой c_ij равен сумме всех попарных произведений элементов, стоящих на одинаковых местах в i-ой строке матрицы A и j-ом столбце матрицы B.Возможно, когда число столбцов 1 матрицы = число строк 2 матрицы.

C_mn =A_mkB_kn

Свойства определителей.

• Если все элементы какой-либо строки (столбца) матрицы равны 0, то ее определитель равен 0.
• Если все элементы какой-либо строки (столбца) матрицы умножить на число l, то ее определитель также умножится на l.
• При транспонировании матрицы ее определитель не изменяется.
• При перестановке двух строк (столбцов) матрицы ее определитель меняет знак на противоположный.
• Если матрица содержит две одинаковые строки (столбца), то ее определитель равен 0.
• Если элементы двух строк (столбцов) матрицы пропорциональны, то ее определитель равен 0.
• Определитель матрицы не изменится, если к элементам какой-либо строки (столбца) матрицы прибавить элементы другой строки (столбца), предварительно умноженные на одно и то же число.

14. Элементарные преобразования строк и столбцов матрицы. Их использование при нахождении определителей.

· Транспонирование матрицы.

· Перестановка двух строк (столбцов).

· Сложение элементов одной строки (столбца) с элементами другой строки (столбца), умноженными на одно и то же число (в частности, вычитание строк).

· Элементарные преобразования 1–3 квадратной матрицы не изменяют значения ее определителя.

· Умножение всех элементов какой-либо строки (столбца) матрицы на число  (увеличивает ее определитель в  раз).

· Вычеркивание нулевой строки (изменяет размер матрицы).

Теорема Кронекера-Капелли.

Система Совместна (имеет хотя бы одно решение) тогда и только тогда, когда Ранг матрицы системы равен рангу расширенной матрицы. Система линейных уравнений имеет решение, если ранг матрицы системы равен рангу расширенной матрицы, причем, если он равен и числу неизвестных, то решение – единственное. Если ранг расширенной матрицы больше ранга матрицы системы, то система решения не имеет

Теоремы Ферма и Ролля,

Ферм: если дифференцируемая на промежутке Х функция достигает наибольшего или наименьшего значения во внутренней точке х0 этого промежутка, то производная функции в этой точке равна 0. Геометрический смысл: в точке наименьшего или наибольшего значения внутри промежутка касательная к графику функции параллельна оси абсцисс.

Ролль: Пусть функция: непрерывна на отрезке, диффиреренцируема на интервале, на концах отрезка принимает одинаковые значения, тогда внутри отрезка существует по крайней мере одна точка, в которой производная равна 0.

Формула Ньютона-Лейбница.

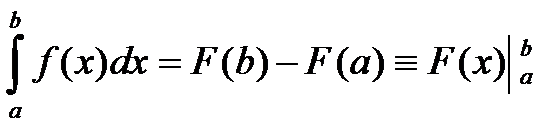
Основные понятия теории вероятностей. Пространство элементарных событий.

Теория вероятностей - математическая наука, изучающая количественные закономерности массовых случайных явлений.

Под случайными явлениями (или событиями) понимаются явления с неопределенным исходом, происходящие при неоднократном воспроизведении некоторого комплекса условий

Опыт – физический процесс, существующий или созданный, протекающий при некотором комплексе условий

Комплекс условий и есть испытание, опыт, а всякое событие есть исход этого испытания

Событие – факт, который может произойти или не произойти в результате опыта

События:

· достоверные

· обязательно должно произойти в результате испытания

· невозможные

· не может произойти в результате испытания

· случайные

· может произойти или не произойти

· несовместные

· появление одного из них в единичном испытании исключает появление другого в этом же испытании

· совместные

· в противном случае.

· единственно возможные

· если в результате испытания должно произойти хотя бы одно из них

· противоположные

· два единственно возможных и несовместных события

· независимые

· появление одного события не зависит от появления или не появления другого

· зависимые

· появление одного события зависит от появления или не появления другого

· равновозможные

· в результате испытания ни одно из этих событий не является объективно более возможным

· полная группа

· единственно возможные и несовместные

· элементарные

· образуют полную группу и равновозможные

Формула полной вероятности.

Если событие A может произойти только при условии появления одного из событий H1, ..., Hn , образующих полную группу, то вероятность события A равна сумме произведений вероятностей каждого из этих событий на соответствующие условные вероятности события A:

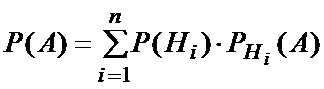
Т.к. Н1,…, Нn – единственно возможные, а А может произойти только вместе с одним из них, то А=Н1А+Н2А+…+ Нn А

Т.к. Н1,…, Нn – несовместные, то по теореме сложения

Р(А)=Р(Н1А)+Р(Н2А)+…+Р( Нn А)

По теореме умножения, Р(НiA)=P(Hi)PHi(A)

Теорема Байеса.

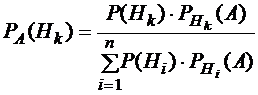
Если существуют попарно исключающие друг друга гипотезы

Н1, ..., Нn , охватывающие все возможные случаи, и если известны вероятности события А при каждой из этих гипотез, то можно найти вероятность справедливости гипотезы Нk при условии, что произошло событие А.

Наступление события A дает новую информацию, благодаря которой можно найти условные вероятности гипотез (PA(Нk), k=1, 2, …, n).

Подход, позволяющий проверять и корректировать после испытания выдвинутые предварительно гипотезы, называется байесовским.

Высказывания и основные операции над ними. Таблицы истинности.

Высказывание – всякое утверждение, о котором объективно и определенно можно сказать, истинно оно или ложно.

· значения истинности высказывания – 1 (истина) и 0 (ложь).

Операции:

• Отрицание. Отрицанием А называется высказывание Ø А («не А»), которое истинно, когда ложно А, и ложно, когда А истинно.

• Конъюнкция. Конъюнкцией (от лат. conjunctio – союз, связь) высказываний А и В называется высказывание А Ù В («А и В»), истинное в том и только в том случае, когда оба высказывания А и В истинны.

• Дизъюнкция. Дизъюнкцией (от лат. disjunctio – различие) высказываний А и В называется высказывание АÚВ («А или В»), ложное в том и только в том случае, когда оба высказывания А и В ложны.

• Импликация.Импликацией (от лат. implico – тесно связаны) высказываний А и В называется высказывание АÞ В («А влечет В», «А имплицирует В», ложное в том и только в том случае, когда А истинно, а В ложно. (если А, то Б)

• Эквиваленция. Эквиваленцией высказываний А и В называется высказывание АÛВ («А эквивалентно В», «эквиваленция А и В», истинное в том и только в том случае, когда высказывания А и В оба истинны или оба ложны.