Влияющие на безопасность полетов

Факторы,

СТАТИСТИЧЕСКИЕ ПОКАЗАТЕЛИ

БЕЗОПАСНОСТИ ПОЛЕТОВ

Для количественной оценки уровня безопасности полетов и выявления его зависимости от свойств авиационной системы ис­пользуют специальные показатели (критерии). В настоящее вре­мя в авиационной практике и исследованиях (анализах) безопас­ности полетов применяют два типа показателей – статистичес­кие и вероятностные.

Статистические показатели обычно выражаются физически­ми величинами или отношением этих величин, получаемых в ре­зультате обработки статистических данных эксплуатации. Ве­роятностные показатели вычисляют методами теории вероятнос­ти аналитическим путем. Строго говоря, статистические и ве­роятностные показатели связаны функционально друг с другом (см. п. 1.3.), поэтому и тот, и другой типы показателей в принципе могут быть рассчитаны и по данным статистики ава­рийности, и аналитическим путем на основе использования ве­роятностных методов. Как правило, их непосредственное вычисление производится так, как указано выше.

Статистические показатели можно разделять на общие и частные, абсолютные и относительные. Общие показатели харак­теризуют уровень безопасности полетов, учитывая интегральное влияние на нее всех факторов, а частные – влияние только отдельных факторов или групп однородных факторов.

Общие абсолютные статистические показатели. К ним отно­сят: абсолютные числа авиационных происшествий 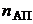, катас­троф 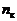, инцидентов 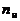, число погибших в АП членов экипа­жей и пассажиров 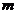, материальный ущерб от АП.

Абсолютные показатели могут быть использованы при дол­госрочном планировании заказов авиационной техники, для уточнения соответствующих статей расходов на развитие авиа­ции, для выявления общих тенденций в динамике аварийности и других случаях.

Потери авиационной техники от АП достаточно велики. Ежегодно в результате аварий и катастроф теряются более десятка ЛА. Все возрастающая стоимость современных боевых ЛА приводит к росту материального ущерба от АП.

При ведении боевых действий авиация наряду с боевыми потерями несет значительные потери от АП (небоевые потери). Это подтверждается опытом второй мировой войны и последую­щих локальных войн и конфликтов. В годы второй мировой вой­ны США потеряли больше самолетов от АП, чем в результате действий противника. В 1983г. во время конфликтов в Гренаде и Ливане, в которые была вовлечена авиация ВМС США, аварий­ность в них возросла более чем в два раза. Резкое увеличение аварийности в период ведения боевых действий объясняется специфическими условиями применения авиации: существенным увеличением нагрузки на летные и наземные экипажи, использо­ванием предельных режимов полета, полетами в сложных ме­теоусловиях и др. Вполне очевидно, что проблема снижения аварийности в период ведения боевых действий является весьма актуальной.

Абсолютные показатели в прямой постановке количествен­но не характеризуют уровень безопасности полетов, так как они зависят от количественного и качественного состава пар­ка ЛА, суммарного налета и т.д. По абсолютным показателям нельзя сравнить уровни БзП различных типов ЛА, родов авиа­ции. От рассмотренных недостатков в определенной мере сво­бодны относительные статистические показатели.

Общие относительные статистические показатели. В воен­ной авиации в качестве относительных показателей используют два типа показателей:

средний налет на одно событие рассматриваемой тяжести 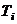, на одно авиационное происшествие 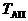, на одну катастрофу 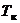, на один инцидент ;

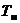среднее число событий рассматриваемой тяжести 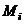, приходящееся на 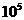часов налета.

Вычисление этих показателей производится по очевидным соотношениям, например:

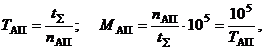(1.1)

где 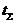– суммарный налет в часах за анализируемый период.

Показатели могут вычисляться как годовые (анализируе­мый период – один календарный год) или как кумулятивные (суммарные). В последнем случае анализируемый период состав­ляет несколько календарных лет. Кумулятивные показатели яв­ляются более достоверными в статистическом смысле и менее подвержены случайным колебаниям по сравнению с годовыми по­казателями.

Справедливость этого положения можно подтвер­дить графиками, приведенными на рис. 1.2 и 1.3. На рис. 1.2 представлены зависимости от суммарного налета кумуля­тивного показателя 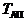для самолетов F-15 и F-16 с начала их эксплуатации, а на рис. 1.3 – зависимости годового пока­зателя 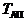от календарного времени в целом для ВВС США и тактической авиации ВВС США.

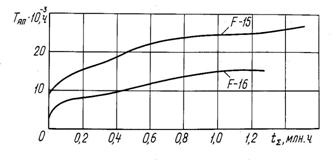
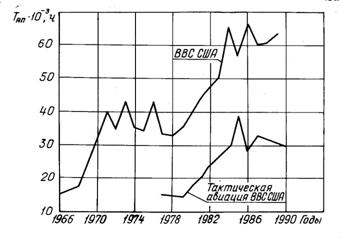Рис. 1.2

Рис. 1.3

Рассмотрим общие тенденции изменения годового среднего налета на одно авиационное происшествие 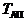как наиболее общие характеристики уровня безопасности полетов на примере дан­ных аварийности по ВВС США (см. рис. 1.3). Анализ графиков позволяет сформулировать выводы, отражающие общие закономер­ности в изменении уровня БзП военных самолетов:

1. Развитие военной авиации сопровождается увеличением среднего налета на одно АП, хотя эта тенденция крайне неравномерная. Периоды роста уровня БзП чередуются с периодами его практи­ческой стабилизации.

2. Для самолетов тактической авиации (штурмовиков, ис­требителей, истребителей-бомбардировщиков) средний налет на одно АП значительно меньше, чем в среднем по парку ЛА. Это объясняется тем, что в составе парка ЛА определенную часть составляют тяжелые самолеты (бомбардировщики, военно-тран­спортные самолеты), для которых средний налет на одно АП значительно больше, чем для легких самолетов.

В гражданской авиации для оценки достигнутого уровня безопасности полетов используют показатели, регламентирован­ные ИКАО (международной организацией гражданской авиации при ООН). Важнейшими из них являются следующие: 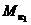, , 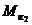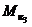– количество катастроф, приходящееся соответственно на 100 млн. километров налета, на 100 тыс. часов налета, на 100 тыс. полетов (посадок); 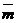– число погибших в ка­тастрофах пассажиров, приходящееся на 100 млн. пассажиро-ки­лометров. На рис.1.4 показана динамика этих 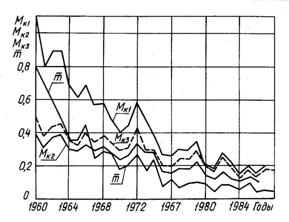показателей по данным ИКАО.

Рис. 1.4

Частные статистические показатели. Общие статистичес­кие показатели имеют интегральный характер и в силу этого не позволяют выявить влияние на уровень БзП отдельных факторов. Эта задача в определенной мере решается при использовании частных показателей. Как и общие показатели, они могут быть абсолютными и относительными.

К абсолютным частным показателям относят 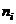, , 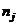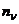– количества событий (аварий, катастроф, АП вообще), соответственно вызванных i-й причиной (фактором), j-й группой причин (факторов), происшедших на n-м этапе поле­та.

К относительным частным показателям относят относи­тельные количества событий, происшедших по указанным выше причинам:

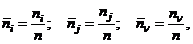
где 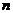– общее количество событий по всем причинам (этапам полета); 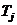– средний налет на одно событие, происшедшее по j-й группе причин (факторов),

.

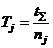В табл. 1.1 приведено распределение в процентах АП по основным группам причин и по этапам полета для военной и гражданской авиации.

Т а б л и ц а 1.1

Группы причин АП	Этапы полета
Ошибки лич­ного состава	Отка­зы авиа- ци­онной техни­ки	Неблаго-прият-ные условия	Причи-ны АП не установ-лены	Взлет и набор высоты	Марш-рут-ный полет	Зона, боевое приме-нение	Заход на посадку и посадка
В о е н н а я а в и а ц и я
60...70	20...30	2...5	2...4	15...20	10...20	30...50	20...40
Г р а ж д а н с к а я а в и а ц и я
60...80	10...25	5...10	5...7	30...35	15...20	¾	50...55

Из данных табл. 1.1 следует:

1. Ошибки личного состава как причины АП являются превали­рующими среди других причин как в военной, так и в граждан­ской авиации. Это подтверждает важность проблемы выявления причин ошибочных действий личного состава с позиций личнос­тного и человеческого факторов.

2. Для военной авиации наиболее аварийные этапы полета: заход на посадку и посадка, полет в зону и боевое примене­ние. Первый этап связан со скоротечностью процессов управления в режиме захода на посадку, дефицитом времени на исправление допущенной ошибки, необходимостью строгого выдерживания задан­ных параметров полета и профиля полета; второй – полет в зо­ну и боевое применение – обусловлен использованием на этих этапах полета режимов полета, близких к предельным, с повы­шенной нагрузкой на летные экипажи и их некоторым отвлече­нием от задач пилотирования при выполнении боевой задачи.

3. Для гражданской авиации наиболее аварийный этап поле­та – заход на посадку и посадка, так как из всех этапов полета этот этап является наиболее сложным по выполнению.

Статистические показатели вычисляются по реальным дан­ным массовой эксплуатации, их главное достоинство – объек­тивность. Однако статистические показатели имеют и ряд недостатков, сужающих область их практического использо­вания. К ним можно отнести:

оценку уровня БзП по статистическим показателям произво­дят тогда, когда АП произошли, то есть они регистрируют прош­лые факты;

статистические показатели невозможно применить для прог­ноза уровня БзП при изменении условий эксплуатации и приме­нения;

по статистическим показателям невозможно дать оценку эф­фективности различных организационных и технических мероп­риятий, направленных на повышение БзП, еще до их практичес­кой реализации;

по статистическим показателям невозможно выявить влия­ние на уровень БзП какого-либо конструктивного или аэродина­мического параметра ЛА, провести оптимизацию уровня БзП с учетом стоимости и эффективности.

Перечисленные недостатки статистических показателей принципиально устранимы или могут быть компенсированы ис­пользованием второго типа показателей – вероятностных.

ВЕРОЯТНОСТНЫЕ ПОКАЗАТЕЛИ

БЕЗОПАСНОСТИ ПОЛЕТОВ

Вероятностные показатели безопасности полетов объектив­но отражают ту закономерность, что авиационное происшествие как потенциально возможный исход конкретного полета являет­ся по своей природе случайным событием в силу случайности возникновения во времени и пространстве полета опасных фак­торов, вызывающих его.

Примем за уровень безопасности выполнения отдельного полета вероятность 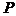благополучного его завершения. Ве­роятность неблагополучного завершения полета, то есть заканчи­вающегося АП, обозначим . Эта вероятность характеризует уровень риска в отдельном полете. Из физических соображений ясно, что

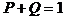. (1.2)

Вероятности 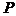и – показатели безопасности полета. Исходя из (1.2) для оценки безопасности полета достаточно знать одну из указанных вероятностей, например .

Вполне очевидно, что безопасность выполнения множества полетов определяется безопасностью выполнения отдельных по­летов. Формализуем связь понятий «безопасность полетов» и «бе­зопасность полета». Если – уровень риска в отдельном по­лете, то для множества, в частности 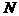, полетов в качестве такого же смыслового критерия может быть принята вероят­ность 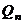, то есть вероятность того, что в 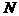полетах произой­дет ровно 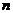АП, где .

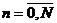Будем полагать, что все полеты идентичны по безопаснос­ти их выполнения, то есть 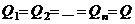. При этом предпо­ложении для вычисления вероятностей 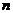АП в 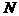полетах можно воспользоваться частной теоремой теории вероятностей о повторении опытов, в соответствии с которой связь 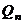и будет определяться биномиальным распределением:

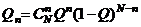, (1.3)

где .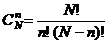

В действительности в общем случае полеты могут произво­диться в неодинаковых условиях, и вероятности благополучного завершения каждого полета меняются от полета к полету. Для вычисления вероятностей появления определенного числа АП в этих случаях нужно пользоваться методикой, основанной на об­щей теореме теории вероятностей о повторении опытов.

Трудности вычисления по формуле (1.3) возрастают с увеличением числа полетов 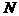. При оценке безопасности поле­тов реально выполняются условия: 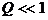; число полетов 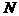достаточно велико. В соответствии с этим с достаточной сте­пенью точности для упрощения вычислительных процедур биноми­альное распределение (1.3) может быть заменено пуассоновским распределением вероятностей:

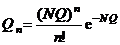. (1.4)

Для вероятности благополучного завершения всех 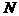полетов, полагая в формуле (1.4) 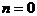, получаем

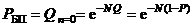. (1.5)

Вероятность 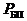по смыслу является показателем безопасности полетов, и, следовательно, формула (1.5) является мате­матическим выражением показателя безопасности полетов 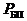через показатель безопасности одного полета 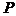, то есть являет­ся формализованной связью понятий безопасности полетов и бе­зопасности полета.

Рассматриваемое в распределении (1.4) число полетов 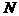реализуется за суммарный налет 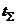, так что 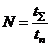, где 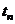– продолжительность одного полета. Учитывая, что в одном полете более одного АП произойти не может, математи­ческое ожидание числа АП на отрезке времени 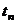формально можно записать в ви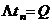де , где 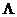– интенсивность по­тока АП, то есть среднее число АП в единицу времени налета. Для всех 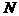полетов математическое ожидание числа АП будет опре­деляться 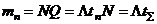и соответственно распределение (1.4) можно записать в виде

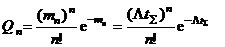. (1.6)

Поток АП, описываемый распределением (1.6), является прос­тейшим, то есть обладает свойствами стационарности, ординар­ности и отсутствия последействия. Для такого потока время 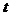между соседними событиями (АП), как известно из теории ве­роятностей, распределено по показательному закону с плот­ностью вероятностей

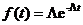. (1.7)

Применяя к выражению (1.7) операцию определения математичес­кого ожидания, вычислим средний налет на одно АП

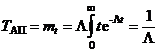. (1.8)

Используя результат (1.8), запишем распределение (1.6) в ви­де

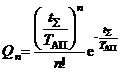. (1.9)

При 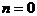получим выражение для показателя безопасности полетов

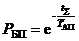. (1.10)

Формула (1.10) определяет связь вероятностного показателя безопасности полетов со статистическим показателем – сред­ним налетом на одно АП.

Из сопоставления формул (1.5) и (1.10) определим, что

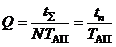. (1.11)

При продолжительности полета 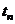один час уровень риска

,

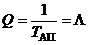то есть численно равен интенсивности потока АП.

Формулы (1.4), (1.9), (1.11) свидетельствуют о том, что при расчетах показателей безопасности полетов для определен­ных значений 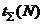достаточно знать один из трех показате­лей , , 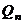, 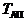а два других определяют по приведенным выше соотношениям.

Приняв обозначения 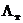, , 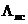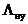– интенсивности потоков АП соответственно из-за отказов авиационной техники, ошибок личного состава и неблагоприятных условий полета и полагая АП по этим факторам независимыми друг от друга собы­тиями, общий показатель безопасности полетов 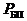можно представить через частные показатели:

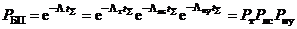, (1.12)

где 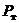, , 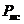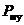– вероятности отсутствия АП за суммарный налет соответственно из-за отказов техники, ошибок личного состава, неблагоприятных условий.

Следует отметить, что соотношения (1.5) и (1.10) приме­нимы не только к оценке вероятности отсутствия АП, но и ве­роятности отсутствия инцидентов, отказов в воздухе, если по­токи этих событий являются простейшими (подчиняются распре­делению Пуассона). В этом случае под (или 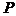) в форму­ле (1.5) нужно понимать вероятность появления (или непоявления) соответствующего события, а под 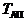в формуле (1.10) - средний налет на одно такое событие.

Связь между вероятностными и статистическими показате­лями безопасности полетов дает возможность решать ряд прак­тических задач, в частности, задавать в вероятностной форме требования к уровню БзП для проектируемого ЛА на основании опыта эксплуатации однотипного ЛА; оценивать эффективность различных мероприятий, направленных на повышение БзП; опре­делять соответствие фактического уровня БзП заданному и др.

Общий подход

Методом перебора гипотез

В основу математической формулировки метода может быть положена формула полной вероятности, предусматривающая рас­смотрение всех физически возможных гипотез, связанных с от­дельными опасными факторами и их комбинациями.

Вероятность благополучного исхода полета при n воз­можных опасных факторах в любых их сочетаниях можно запи­сать в виде

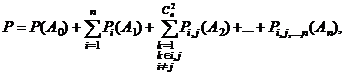(1.15)

где 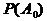– вероятность того, что не возникает ни один опасный фактор; 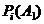, 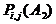– вероятность того, что возникают только один опасный фактор и исход полета будет благополучным, два опасных фактора и т.д.

Слагаемые в (1.15) при условии, что факторы независи­мы, определяются следующими выражениями:

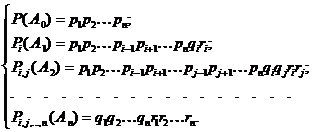(1.16)

Вероятность авиационного происшествия определяется из очевидного условия, что каждый последующий опасный фак­тор во время полета физически возможен, если перед этим опасные факторы не возникали, а если и возникали, то они парировались. В соответствии с этим условием получим

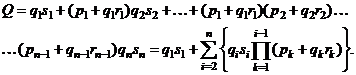(1.17)

Вообще говоря, уровень риска можно вычислить и более простым способом – как вероятность противоположного события, то есть

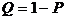. (1.18)

Рассмотрим элементарный пример. Определить выражение для 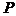при воздействии двух независимых факторов. В соответ­ствии с (1.15) и (1.16) имеем

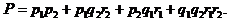(1.19)

Нетрудно заметить, что выражение (1.19) может быть представ­лено произведением

.

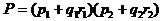Обобщая этот результат для n независимых факторов, полу­чим

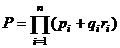. (1.20)

Формула (1.20) является компактной записью развернутых выра­жений, представленных (1.15) и (1.16).

С учетом воздействия на ЛА только одного фактора, кото­рый может возникать в полете неоднократно, например m раз, на основании (1.20) имеем

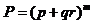. (1.21)

Учитывая, что 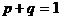, , 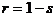из (1.21) следует

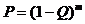, (1.22)

где 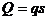– уровень риска при однократном появлении фактора.

Раскладывая функцию (1.22) в ряд и ограничиваясь первыми двумя членами разложения, получим

.

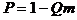Заметим, что это соответствует разложению функции 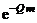при ограничении его первыми двумя членами разложения. Следова­тельно, приближенно можно представить

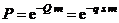. (1.23)

Пример. При выполнении маневра вероятность ошибки лет­чика 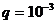, условная вероятность ее непарирования 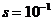. Оценить безопасность выполнения 100 таких манев­ров.

Расчеты проводим в соответствии с формулой (1.22):

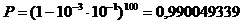
и формулой (1.23) :

.

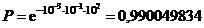Как видно, погрешность от замены точной формулы приближен­ной сказывается только начиная с седьмого знака после запя­той.

До сих пор все рассуждения и выкладки относительно ме­тодики расчета показателе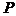й и велись без учета этапнос­ти выполнения полета. К решению этой задачи можно подойти, рассматривая вероятности благополучного 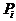и неблагополуч­ного 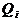исходов по каждому i-му фактору с учетом этапности выполнения полета.

Для фактора i-го типа последовательность событий по этапам полета, связанная с возможностью его появления на од­ном из этапов, может быть представлена графом (деревом состояний), изображенным на рис. 1.6. Граф характеризует многошаговый процесс (1,..., 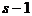, ,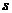..., 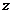) перехода системы из од­ного состояния (события) к другому с учетом возможности появления i-го фактора на рассматриваемом этапе, начиная от первого и заканчивая последним. На стрелках графа простав­ляются вероятности перехода от одного состояния к другому, при этом должно соблюдаться условие: сумма вероятностей на всех стрелках, выходящих из одного состояния, должна рав­няться единице.

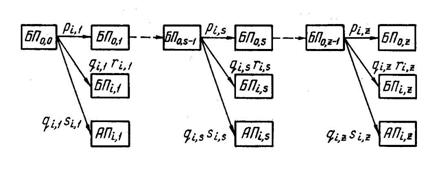
Рис. 1.6

На рис. 1.6 обозначено: 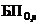– событие непоявления i-го фактора на s-м этапе; 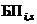, 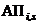– события благополучного и неблагополучного исхо­дов при появлении i-го фактора на s-м этапе.

Вероятности этих событий определяются как произведение всех вероятностей, указанных на стрелках, начиная от рас­сматриваемого события и заканчивая начальным 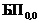. Заметим, что вероятность 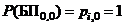, то есть в начале полета i-й фактор отсутствует.

В соответствии с изложенным

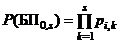; (1.24)

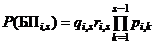; (1.25)

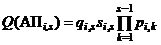. (1.26)

Для всех z этапов полета показател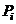и и 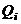с учетом воздействия только одного i-го фактора на основании формул (1.24) – (1.26) приобретают вид:

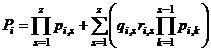; (1.27)

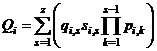. (1.28)

По всем n факторам, учитывая их независимость, имеем

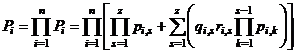. (1.29)

Уровень риска за полет с учетом возможного воздействия всех n факторов определим как

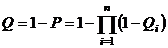. (1.30)

Раскрывая почленно произведение 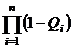, на основании формулы (1.30) определяем

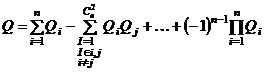. (1.31)

Условие нормировки 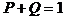выполняется. Учитывая, что 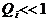, в ряде случаев формулу (1.31) можно ограничить только первым слагаемым, то есть

.

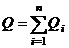В заключение укажем, что метод перебора гипотез при расчете показателе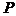й и может применяться как для дис­кретных, так и непрерывных факторов, как зависимых, так и независимых.

При расчете показателе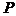й и для зависимых факторов целесообразно пользоваться графической интерпретацией пере­хода системы от одного состояния (события) к другому, так как умозрительный перебор всех гипотез, связанных с появле­нием отдельных факторов и их комбинаций, затруднен. Граф (де­рево состояний) должен строиться по правилам, реализованным при построении графа, показанного на рис. 1.6.

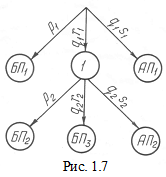В качестве примера рассмотрим случай воздействия двух зависимых факторов: второй фактор может появиться при условии, если первый уже появился. Граф для этого случая указан на рис. 1.7. Как видно из него, сложные события 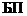и 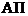представляются суммами событий: ; .

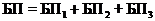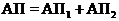Вероятности элементарных событий равны:

.

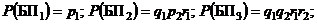
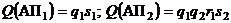Отсюда .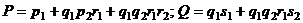

В правильности выкладок читатель может убедиться по условию

.

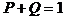Безопасного полета

Оценка БзП при воздействии на ЛА факторов, вероятность появления которых зависит от времени полета, может быть проведена на основе представления переходов системы от од­ного состояния к другому под воздействием опасных факторов моделью марковского процесса со счетным множеством состоя­ний и непрерывным временем. Факторы при этом могут быть как зависимые, так и независимые, однократно возникающие и мно­гократно повторяющиеся, с зависимыми и независимыми послед­ствиями, то есть такая модель позволяет получить оценку БзП с учетом воздействия на ЛА обширного класса опасных факто­ров. Допустим, что все возможные в полете особые ситуации, вызванные опасными факторами, образуют счетное множество 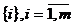. В зависимости от успешности действий экипажа по парированию последствий опасных факторов множеству 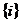бу­дут соответствовать два подмножества: 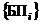– благополуч­ных исходов и 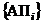– неблагополучных исходов полета.

Обозначим вероятности этих исходов соответственно 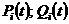. Так как события из множества 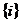для текущего момента времени полета являются несовместным, то на основании теоремы сложения вероятностей можно записать

,

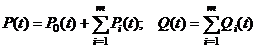где 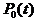– вероятность пребывания системы в нормальном состоянии.

Неизвестные вероятности 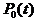, , 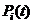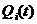вычисляются по модели марковского процесса смены состояний рас­сматриваемой системы.

Для обоснования возможности применения такой модели ис­пользуются следующие допущения:

1. События парирования или непарирования возникают однов­ременно с появлением опасных факторов, вызывающих особую си­туацию.

2. Последовательность возникновения особых ситуаций i-го типа является простейшим потоком с интенсивностью 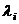. Соответствующие ему потоки благополучных и неблагополучных исходов в силу принятого допущения также являются простейши­ми. Их интенсивности соответственно равны , .

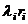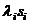3. Отказавшие в полете элементы не восстанавливаются, а ошибки операторов не повторяются.

Напомним, что в силу ранее принятого допущения (см. п. 1.4) ситуация в начале полета является нормальной, то есть опасные факторы отсутствуют. Для расчета вероятностей 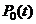, , 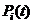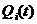марковский процесс со всеми выявленными и реально возможными в полете состояниями системы представляется наг­лядно в виде графа состояний (рис. 1.8). В узлах этого гра­фа обозначаются состояния системы (исходы полета); вершина графа (состояние 0) соответствует нормальной ситуации. Сос­тояния системы, в которые она переходит непосредственно из нулевого состояния вследствие появления опасных факторов, 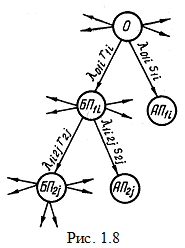на­зываются состояниями первого уровня, а состояния, возникающие из состояний первого уровня, – состояниями второго уровня и т. д.

Обозначим эти состояния: на первом уровне по i-му фак­тору – 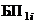, 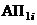– соответственно для благополучных и неб­лагополучных исходов; на втором уровне по j-му фактору – 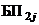, 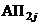и т.д. На стрелках графа проставляются интенсив­ности перехода от одного состояния к другому: при переходе от нулевого состояния к состояниям первого уровня – 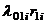; ; 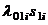при переходе от состояний первого уровня к состояниям второго уровня – 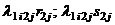и т.д.

Дифференциальные уравнения для определения неизвестных вероятностей состояний составляют по определенному правилу:

число уравнений равно числу состояний (исходов), размечен­ных на графе;

в левой части уравнения стоит производная вероятности дан­ного состояния, а правая часть содержит столько членов, сколько стрелок связано с данным состоянием;

если стрелка выходит из этого состояния, то соответствующий член уравнения имеет знак «минус», если она направлена в состояние – «плюс»;

каждый член уравнения равен произведению интенсивности перехода, соответствующей данной стрелке, на вероятность того состоя­ния, из которого стрелка исходит.

Для краткости обозначим суммарные интенсивности исходов из соответствующих состояний 0, 1i, 2j через

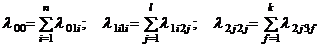. (1.32)

В (1.32) 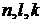– числа факторов, которые могут вывести систему соответственно из нулевого состояния, из i-го состоя­ния первого уровня, из j-го состояния второго уровня. Соот­ношения (1.32) учитывают, что .

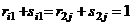Воспользовавшись указанным выше правилом, составим диф­ференциальные уравнения для вероятностей состояний, соответ­ствующих графу на рис. 1.7:

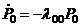; (1.33)

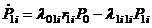; (1.34)

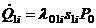; (1.35)

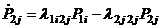; (1.36)

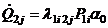. (1.37)

Система дифференциальных уравнений (1.33) – (1.37) ре­шается при следующих начальных условиях:

, , .

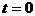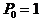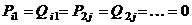В первую очередь решается уравнение для вероятности ну­левого состояния; затем, используя этот результат, произво­дится решение уравнений для вероятностей состояний первого уровня и т.д. Для оценки безопасности полета достаточно ре­шить только уравнения для вероятностей благополучных исхо­дов, но для проверки правильности решения по условию 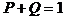необходимо решать всю систему дифференциальных уравнений.

Оценка БзП с учетом состояний только первого уровня. Сложность графа состояний и число возможных уровней состоя­ний, которые необходимо учитывать при оценке безопасности полета, определяются характером рассматриваемой задачи. В частности, для состояний, связанных с отказами резервирован­ных систем, граф состояний должен иметь как минимум два–три уровня.

Наибольшее влияние на уровень БзП оказывают состояния первого уровня, так как они вызваны п<