Кинематические диаграммы движения ползуна

На планах положений механизма за начальную точку отсчета перемещений ползуна берем точку В_о. Принимаем масштаб перемещений ползуна по оси ординат равным по величине масштабу длин планов положений механизма: =0,002 ( ).

Масштаб углов поворота кривошипа

( ).

Время одного полного оборота кривошипа

= =0,0375( ).

Масштаб времени

=0,0000104 ( ).

Масштаб по оси ординат диаграммы скоростей:

= =3.846 ( ).

Принимаем полюсное расстояние H₂=50 мм. Масштаб по оси ординат диаграммы ускорений:

= =7396,15( ).

Планы скоростей механизма

Строим 12 планов скоростей для каждого из 12 положений механизма.

Вычисляем угловую скорость входного звена 1:

( ).

Для определения скорости точки А составляем векторное уравнение скоростей: . Так как , то .

Определяем величину этой скорости:

Принимаем Тогда масштаб плана скоростей будет

Для определения скорости точки В составляем систему двух векторных уравнений скоростей:

,

.

Приравниваем правые части этих двух уравнений, так как левые части их равны:

.

Так как , то полученное уравнение можно представить в виде

.

Для определения скорости точки С составляем систему двух векторных уравнений скоростей: ,

.

Приравниваем правые части этих двух уравнений, так как левые части их равны:

.

В уравнении точка С₆ - это неподвижная точка стойки 6, которая в рассматриваемое мгновение совпадает по положению с подвижной точкой С ползуна 5.

Так как , то полученное уравнение можно представить в виде

.

Планы ускорений механизма

Строим план ускорений для того положения механизма, для которого по заданию дано значение угла 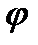=30^о поворота кривошипа.

Для определения ускорения точки А составляем векторное уравнение ускорений:

.

Величину тангенциальной составляющей ускорения определяем по формуле

,

Так как и то .

Величину этого ускорения определяем по формуле

.

Принимаем Тогда масштаб плана ускорений будет

Составляем систему двух векторных уравнений ускорений:

;

.

Приравниваем правые части этих двух уравнений, так как левые части их равны:

.

Вычисляя Кориолисово ускорение, видим, что оно равно нулю, так как ползун 3 и направляющая стойки 6, входящие в поступательную кинематическую пару, вращательного движения совершать не могут:

Так как и , то векторное уравнение для ускорений точек механизма можно представить в виде .

Определяем величину и направление нормальной составляющей ускорения :

,

где

Определяем длину вектора с учетом принятого масштаба плана ускорений:

( ).

По заданию имеем следующее соотношение размеров длин на схеме механизма:

AS₂/AB=0,45

По теореме подобия для планов ускорений аналогичное соотношение соответствующих размеров должно быть и на плане ускорений. Отсюда

( ).

Ускорения центров тяжести шатуна и ползуна:

1882,0544 ,

.

Ускорение точки С необходимо определить. Ускорения же двух остальных точек известны: ускорение точки А найдено, и его вектор на плане ускорений уже проведен, ускорение же точки С₆ стойки равно нулю. Составляем систему двух векторных уравнений ускорений:

;

.

Приравниваем правые части этих двух уравнений, так как левые части их равны:

.

Вычисляя кориолисово ускорение, видим, что оно равно нулю, так как ползун 5 и направляющая стойки 6, входящие в поступательную кинематическую пару, вращательного движения совершать не могут:

Так как и , то векторное уравнение для ускорений точек механизма можно представить в виде

.

Определяем величину и направление нормальной составляющей ускорения : ( ) ,

где ( ).

Определяем длину вектора с учетом принятого масштаба плана ускорений:

( ).

По заданию имеем следующее соотношение размеров:

AS₄/AС=0,45.

По теореме подобия для планов ускорений аналогичное соотношение

соответствующих размеров должно быть и на плане ускорений. Отсюда

( ).

Ускорения центров тяжести шатуна и ползуна:

,

.

Силовой расчет механизма