Скалярное произведение векторов: определение, свойства и геометрический смысл. Скалярное произведение векторов, заданных координатами.
Скалярным произведениемвекторов 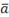 и
и 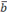 называется число (скаляр) обозначаемое символом
называется число (скаляр) обозначаемое символом 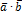 , равное произведению длин этих векторов на косинус угла между ними:
, равное произведению длин этих векторов на косинус угла между ними:
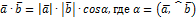 (9.1)
(9.1)
отсюда следует 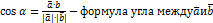 .
.
Свойства:
1) 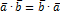
2) 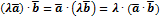 ,
, 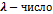
3) 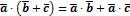
4) 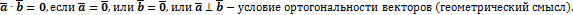
Если векторы заданы координатами
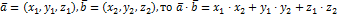 (9.3)
(9.3)
и тогда 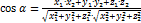
Относительно ортов осей координат:
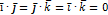
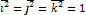
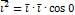
Геомет.смысл:Алгебраическое значение проекции вектора 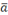 на вектор
на вектор 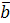 вдоль прямой,перпендикулярно
вдоль прямой,перпендикулярно 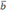 ,очевидно равно |
,очевидно равно | 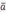 | cos (
| cos ( 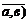 и |
и | 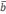 | cos (
| cos ( 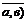 .
.
Векторное произведение векторов: определение, свойства и геометрический смысл модуля. Векторное произведение векторов, заданных координатами.
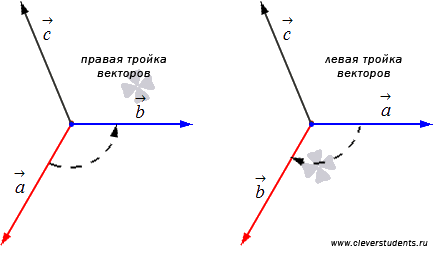
Тройка векторов 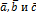 называется правой, если после их приведения к общему началу кратчайший поворот от
называется правой, если после их приведения к общему началу кратчайший поворот от  видится в положительном направлении, т.е. против часовой стрелки, а в противном случае левой.
видится в положительном направлении, т.е. против часовой стрелки, а в противном случае левой.
Векторным произведение векторов 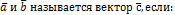
1) векторы 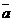 и
и 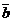 и
и 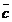 образуют правую тройку
образуют правую тройку
2) перпендикулярен векторам 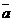 и
и 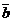 , т.е.
, т.е. 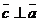 и
и 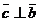 ;
;
3) 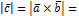 площади параллелограмма, построенного на векторах a ̅ и b ̅
площади параллелограмма, построенного на векторах a ̅ и b ̅
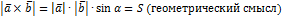
Свойства:
1) 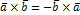 (антиперемистительность)
(антиперемистительность)
2) 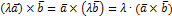 ,
, 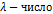
3) 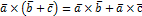
4) 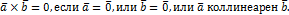
5) относительно ортов осей:
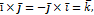
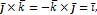
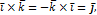
Если 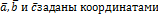
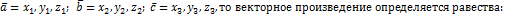
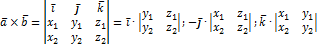
Смешанное произведение векторов: определение, свойства и геометрический смысл. Смешанное произведение по координатам векторов.
Смешанное произведение трех векторов 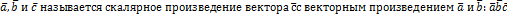 (основное обозначение смешанных векторов)
(основное обозначение смешанных векторов) 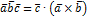
1. 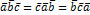 (круговое свойство)
(круговое свойство)
2. 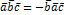
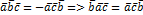
3. 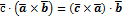
4. 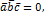 если любой один вектор нулевой, либо два вектора коллинеарны, либо все три компланарны.
если любой один вектор нулевой, либо два вектора коллинеарны, либо все три компланарны.
5. 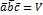 параллелепипеда, построенного на этих векторах. (геометрический смысл)
параллелепипеда, построенного на этих векторах. (геометрический смысл)
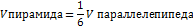
Если 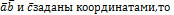
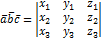
Найти объемы параллелепипеда и пирамиды, построенных на векторах:
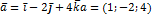
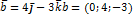
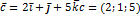
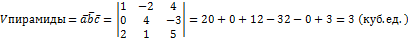
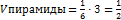 (куб.ед.)
(куб.ед.)
Уравнение прямой на плоскости, проходящей через две точки.(с выводом)
Пусть 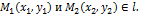
M (x,y) – текущая точка l. Если 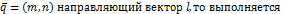 каноническое уравнение.
каноническое уравнение.
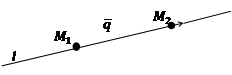 |
Ясно, что 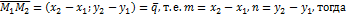
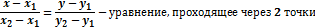
Задача
Составить общее уравнение прямой, проходящей через 2 точки:
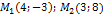
Имеем:
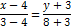
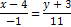
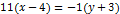
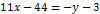
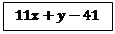 |
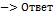
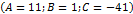
Общее уравнение прямой на плоскости и его исследование. Нормальный вектор прямой. Уравнение прямой «в отрезках». (с выводом)
Теорема: любая прямая lна плоскости.
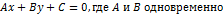 не равны 0 и наоборот линейное уравнение
не равны 0 и наоборот линейное уравнение 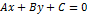 относительно переменных xиyопределяет на плоскости прямую.
относительно переменных xиyопределяет на плоскости прямую.
Определение:
Вектор 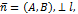 называется нормальным векторомlили нормалью.
называется нормальным векторомlили нормалью.
1. С = 0: 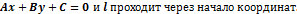

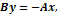 y
y
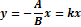
2. В = 0: 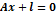
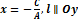 y=0
y=0
3. 
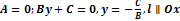 x
x
4. 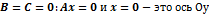
5. 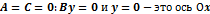 x=0
x=0
 Уравнение прямой «в отрезках».
Уравнение прямой «в отрезках».
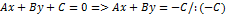
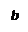
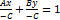
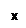
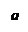

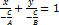
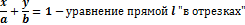
Условие коллинеарности векторов. Понятие направляющего вектора прямой. Каноническое уравнение прямой (с выводом).
Два вектора называются коллинеарными, если они лежат на одной прямой либо на параллельных прямых.
Условия коллинеарности
Ø Два вектора a и b коллинеарны, если существует число n такое, что
a = n · b
Ø Два вектора коллинеарны, если отношения их координат равны.
Ø Два вектора коллинеарны, если их векторное произведение равно нулевому вектору.
Канон –от греч.в переводе означает типовое, образцовое.
Любой вектор лежащий на прямой l либо на 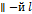 прямой, называется направляющим вектором l.
прямой, называется направляющим вектором l.
Рассматривается прямая l.
Пусть 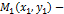 фиксированная точка на прямой. М – текущая точка, т.е. произвольная.
фиксированная точка на прямой. М – текущая точка, т.е. произвольная.
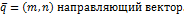
 |
Тогда векторы 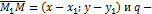 коллинеарны, а значит их соответствующие координаты должны быть пропорциональны.
коллинеарны, а значит их соответствующие координаты должны быть пропорциональны.
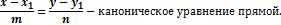
Если 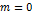 , то
, то 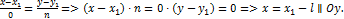
Если 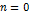 , то аналогично
, то аналогично