Построение трендовых моделей для прогноза стоимостей активов
После измерения периодических доходностей активов за некоторый временной интервал (скажем, квартальную доходность за 4 года) перед инвестором стоит задача спрогнозировать будущие доходности на дальнейший период времени. Для такого рода прогнозов возможно построение трендов – кривых изменений величин доходности.
Рассмотрим временной ряд
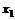 | 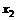 | … | 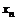 |
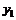 | 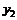 | … | 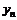 |
Требуется определить линию тренда 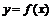 . Функция
. Функция 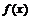 может быть линейной, квадратичной, кубической и т.д. Вид функции известен, неизвестны параметры, входящие в эту функцию
может быть линейной, квадратичной, кубической и т.д. Вид функции известен, неизвестны параметры, входящие в эту функцию 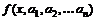 . Параметры
. Параметры 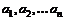 определяются с помощью метода наименьших квадратов (МНК), который заключается в следующем: параметры определяются из условия минимума суммы квадратов отклонений теоретических значений функции
определяются с помощью метода наименьших квадратов (МНК), который заключается в следующем: параметры определяются из условия минимума суммы квадратов отклонений теоретических значений функции 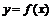 от данных, т.е. из условия
от данных, т.е. из условия
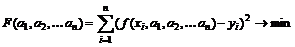 .
.
Для решения поставленной задачи приравниваются к нулю частные производные по всем параметрам. Решением полученной системы будет точка, подозрительная на экстремум, которую необходимо проверить на минимум с помощью критерия Сильвестра.
Для проверки правильности подбора модели необходимо проанализировать среднюю ошибку аппроксимации (среднее значение относительной погрешности)
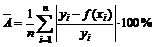 .
.
Также для анализа выбранной модели используют квадрат линейного коэффициента корреляции, который характеризует долю дисперсии результативного признака, объясняемую регрессией, в общей дисперсии. Другими словами, естественными оценками ожидаемого значения и дисперсии случайной величины являются выборочное среднее и выборочная дисперсия. Для величины Х выборочное среднее и выборочная дисперсия равны
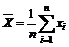 ,
,
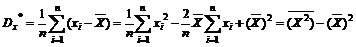 .
.
Для величины Y выборочное среднее и выборочная дисперсия равны
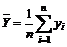 ,
,
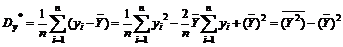 .
.
Естественной оценкой ковариации случайных величин 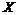 и
и 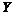 является выборочная ковариация
является выборочная ковариация
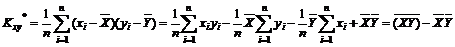 .
.
Тогда квадрат линейного коэффициента корреляции (выборочного) имеет вид
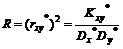 .
.
Предположим, что функция 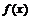 - линейная, то есть имеет вид
- линейная, то есть имеет вид 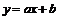 , где
, где 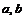 - некоторые неизвестные числа. Последнее – это линейная регрессионная модель.
- некоторые неизвестные числа. Последнее – это линейная регрессионная модель.
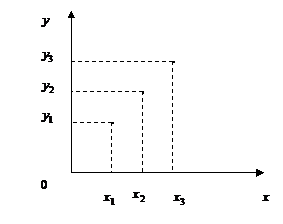
Рис 1.4.1. Линейная модель
Будем минимизировать функцию
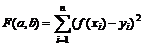
или
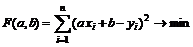 .
.
Для нахождения коэффициентов 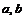 необходимо решить систему уравнений
необходимо решить систему уравнений
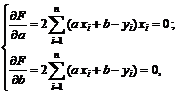
или
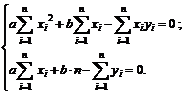
Воспользуемся методом Крамера решения системы линейных алгебраических уравнений. Определители
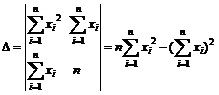 ,
,
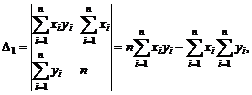
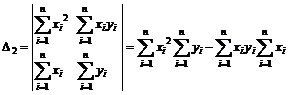 .
.
Таким образом, коэффициенты будут вычисляться по формулам
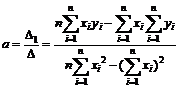 ,
,
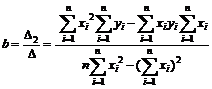 .
.
Пример 1.4.1. Известны значения стоимости акций на начало каждого из часов работы биржи
| 10,5 |
Требуется спрогнозировать цену акции на начало 6 часа с помощью линейной линии тренда и построить график.
Решение. Запишем следующие данные в виде таблицы
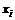 | 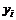 | 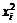 | 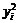 | 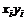 |
| 10,5 | 110,25 | 31,5 | ||
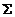 =15 =15 | 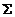 =54,5 =54,5 | 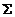 =55 =55 | 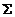 =596,25 =596,25 | 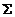 =166,5 =166,5 |
Тогда получаем коэффициенты
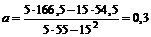 ,
, 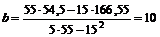 .
.
Таким образом, линейная трендовая модель имеет вид 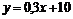 . График этой функции изображен на рис. 1.4.2
. График этой функции изображен на рис. 1.4.2

Рис.1.4.2. Зависимость стоимостей акций от времени
Средняя ошибка аппроксимации равна
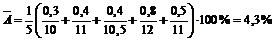 .
.
Коэффициент корреляции равен
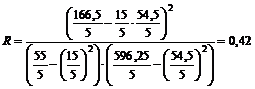 .
.
Иногда бывает необходимо использовать более сложные зависимости, чем просто прямая линия. Рассмотрим процедуру, которая позволяет построить соответствующую кривую. Будут использоваться статистические данные за предыдущие периоды времени для нахождения параметров 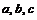 , например, из уравнения квадратичной регрессии
, например, из уравнения квадратичной регрессии
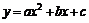 .
.
|
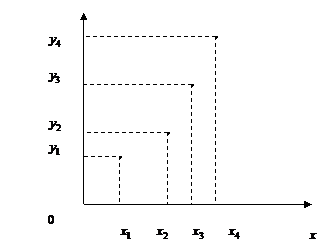
Рис.1.4.3. Квадратичная модель
Аналогично линейному случаю будем решать задачу
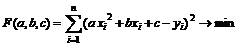 .
.
Искомые коэффициенты 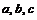 будут решением системы
будут решением системы
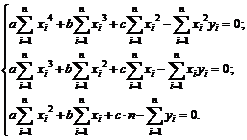
Упражнения
1. Известны цены акции за последние четыре месяца: 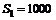 ,
, 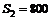 ,
, 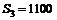 ,
, 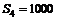 . Спрогнозировать цену акции на последующее три месяца. Построить график.
. Спрогнозировать цену акции на последующее три месяца. Построить график.
2. Результаты сравнения доходностей двух акций 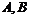 за май, июнь, июль, август приведены в таблице
за май, июнь, июль, август приведены в таблице
| А | 0,1 | 0,15 | 0,13 | 0,2 |
| В | 0,13 | 0,13 | 0,15 | 0,18 |
В сентябре Иванов решил купить одну из имеющихся акций. Какое решение необходимо ему принять, предполагая, что доходности акций зависят от времени линейно. Построить графики.
3. Решить предыдущую задачу для случая квадратичной зависимости. Оценить ошибку аппроксимации для линейной и квадратичной модели. Сделать вывод.
4. Спрогнозировать стоимость актива на конец недели, если известны его стоимости за понедельник-пятницу
| Пн | Вт | Ср | Чт | Пт |